Связь стандартного отклонения со среднеквадратичными значениями

В данной статье исследуется интересная связь между важным статистическим параметром и одним из фундаментальных аналитических инструментов электротехники.

Если вы только присоединились к этой серии статей о статистике в электротехнике, возможно, вы захотите начать с первой статьи, посвященной статистическому анализу, и просмотра второй об описательной статистике. Совсем недавно мы коснулись компенсации размера выборки при вычислении стандартных отклонений, уделяя особое внимание коррекции Бесселя.

В данной статье мы будем основываться на обсуждении стандартного отклонения в предыдущей статье, которое фиксирует усредненную мощность случайных вариаций в наборе данных или в оцифрованном сигнале. Эта усредненная мощность выражается в виде амплитуды, например в вольтах, а не в ваттах.

Инженеры-электронщики постоянно имеют дело со случайными отклонениями. Мы называем их шумом, и они гарантируют, что какой бы хорошей погода ни была, нам будет на что пожаловаться.

Для расчета стандартного отклонения мы используем следующую формулу:

\[\sigma=\sqrt{\sigma^2}=\sqrt{\frac{1}{N-1}\sum_{k=0}^{N-1}(x[k]-\mu)^2}\]

Среднеквадратичное значение (RMS, Root Mean Square)

Большинство из нас, вероятно, впервые узнали о значениях RMS в контексте анализа сигналов переменного тока. В системах переменного тока среднеквадратичное значение напряжения или тока часто более информативно, чем значение, определяющее пиковое напряжение или ток, потому что RMS является более прямым путем к определению рассеиваемой мощности.

Мы не можем использовать пиковое значение напряжения или тока при расчете рассеиваемой мощности, потому что напряжение или ток постоянно меняются, и, следовательно, мгновенная рассеиваемая мощность также изменяется. Расчет на основе пикового значения приведет к завышению усредненной по времени мощности.

Среднеквадратичные значения позволяют рассчитывать рассеиваемую мощность, как если бы мы работали со значениями постоянного тока. Конкретнее, среднеквадратичное значение синусоидального напряжения или тока равно амплитуде сигнала постоянного напряжения или тока, которая создаст такое же количество усредненной по времени рассеиваемой мощности.

Батарея 12 В, подключенная к резистору 10 Ом, будет генерировать 12²/10 = 14,4 Вт (мгновенной и средней) мощности. Если мы заменим батарею на источник переменного напряжения со среднеквадратичным значением напряжения 12 В, (средняя) мощность будет такой же.

Когда мы работаем с синусоидальными сигналами, вычислить среднеквадратичные значения просто: мы просто делим пиковое значение на \(\sqrt{2}\). Следующая диаграмма представляет собой интересную иллюстрацию этой взаимосвязи.

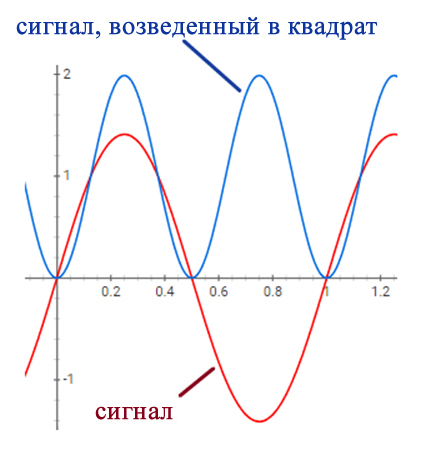
Мощность пропорциональна квадрату напряжения или тока. Постоянное напряжение 1 В, поданное на цепь с сопротивлением R, будет создавать 1²/R=1/R Вт мощности. Взглянув на рисунок выше, мы можем видеть, что синяя кривая имеет среднее значение 1; таким образом, поскольку синяя кривая равна квадрату красной кривой, средняя мощность, генерируемая красной кривой, также будет равна 1/R.

Теперь обратите внимание на пиковое значение красной кривой: оно равно \(\sqrt{2}\) (приблизительно 1,4). Это подтверждает, что нам нужно разделить пиковое значение на \(\sqrt{2}\), чтобы определить значение, которое даст заданную среднюю мощность при применении стандартной формулы V²/R или I²R.

Полный расчет среднеквадратичного значения (RMS)

Тем из нас, кто часто работает с электрическими системами переменного тока, необходимо помнить, что среднеквадратичные значения не ограничиваются синусоидальными сигналами. Кроме того, математическая процедура, которая создает среднеквадратичное значение, значительно сложнее, чем деление на \(\sqrt{2}\)

Так уж получилось, что с синусоидами процедура эквивалентна делению на \(\sqrt{2}\). Это упрощение не применяется к другим типам сигналов, таким как сигналы прямоугольной формы, сигналы треугольной формы или шум.

Фактическое вычисление RMS, то есть вычисление, которое мы применяем к сигналам в целом, выражается следующим образом:

\[X_{RMS}=\sqrt{\frac{1}{T_2-T_1}\int_{T1}^{T2}x(t)^2dt}\]

Эта же процедура словами: предположим, что x(t) – это сигнал во временной области, периодический в интервале от времени T₁ до времени T₂. Мы возводим в квадрат x(t), интегрируем этот возведенный в квадрат сигнал по соответствующему интервалу, делим интегрированное значение на длину интервала и затем извлекаем квадратный корень.

Интегрирование от T₁ до T₂ с последующим делением на (T₂–T₁) аналогично суммированию всех значений сигнала и делению на количество этих значений. Другими словами, выполнение этих двух шагов является эквивалентом во временной области для вычисления среднего арифметического для набора данных. Таким образом, мы извлекаем квадратный корень из среднего значения возведенного в квадрат сигнала: среднеквадратичное значение.

Среднеквадратичное значение (RMS) для дискретных данных

Как преобразовать приведенную выше формулу во что-то, что можно применить к дискретным данным? Другими словами, как мы можем вычислить среднеквадратичное значение оцифрованного сигнала?

Давайте посмотрим на это так: сначала, вместо функции (например, x(t)), мы возводим в квадрат отдельные значения (например, x[1], x[2], x[3] и т.д.). Затем, когда мы переходим от сигнала, непрерывного по времени, к сигналу, дискретному времени, интегрирование становится суммированием, а временной интервал становится «интервалом» точек данных, то есть количеством точек данных, которые были суммированы. И в конце у нас идет квадратный корень, который не меняется.

Таким образом, мы можем записать наш расчет среднеквадратичного значения (RMS), дискретного по времени, следующим образом:

\[X_{RMS}=\sqrt{\frac{1}{N}(x[1]^2 + x[2]^2 + ... + x[N]^2)}\]

Это начинает казаться знакомым? Мы возводим значения в квадрат, суммируем их, делим на количество значений и извлекаем квадратный корень.

Есть только два отличия между этой процедурой и процедурой, которую мы используем для расчета стандартного отклонения:

• В случае RMS мы делим на N; со стандартным отклонением мы (обычно) делим на N–1. Мы можем игнорировать эту разницу, потому что использование N–1 – это просто попытка компенсировать небольшой размер выборки (для получения дополнительной информации смотрите предыдущую статью).
• В случае RMS мы возводим в квадрат точки данных; в случае стандартного отклонения мы возводим в квадрат разницу между каждой точкой данных и средним значением.

Если мы пытаемся установить связь между среднеквадратичным значением и стандартным отклонением, второе различие может показаться решающим.

Однако учтите следующее: если среднее значение равно нулю, как это часто бывает в электрических сигналах, не будет никакой разницы между вычислением RMS и вычислением стандартного отклонения. Другими словами, для сигнала без смещения по постоянному току стандартное отклонение сигнала также равно среднеквадратичному значению.

Заключение

Я не собираюсь пытаться исследовать полное значение этой связи между стандартным отклонением и среднеквадратичным значением. Тем не менее, прежде чем мы закончим, я хочу упомянуть два интересных момента, которые вытекают из обсуждения выше.

Во-первых, стандартное отклонение дает нам среднеквадратичное значение сигнала «с развязкой по постоянному току»: мы можем рассчитать стандартное отклонение, когда смещение сигнала по постоянному току не имеет значения, и это дает нам среднеквадратичное значение только переменной составляющей.

Во-вторых, стандартное отклонение можно интерпретировать как количественную оценку шума, а анализ шума тесно связан со среднеквадратичным значением.

Теги