Введение в нормальное распределение в электротехнике
В данной статье рассматриваются важные характеристики основного статистического распределения, и объясняется значение функции плотности вероятности.
Данная статья является продолжением нашей серии статей о статистике в электротехнике. Первые две статьи заложили основу нашего обсуждения, посвященного статистическому анализу и описательной статистике.
Затем мы рассмотрели среднее отклонение, стандартное отклонение и дисперсию в обработке сигналов, уделяя особое внимание компенсации размера выборки при вычислении стандартных отклонений. В предыдущей статье мы дополнительно экстраполировали наше понимание стандартного отклонения, исследуя его связь со среднеквадратичными значениями.
В данной статье мы расскажем о месте нормального распределения в электротехнике, в частности при оценке функции плотности вероятности.
Что такое нормальное распределение?
Если вы неоднократно измеряете величину, которая изменяется более или менее случайным образом, (уровни напряжения шума, фактические значения сопротивления резисторов 47 кОм, результаты тестов в классе, длину травинок на лужайке и т.д.), вероятно, что по мере накопления всё большего количества данных распределение значений будет постепенно напоминать форму, показанную ниже.
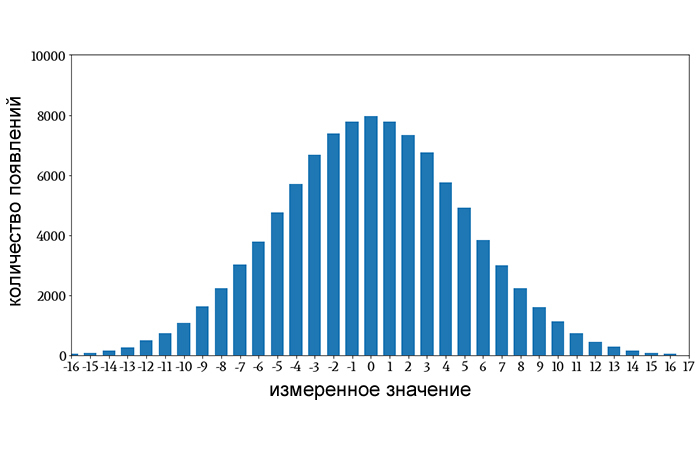
Это называется нормальным или гауссовым распределением. Оно похоже на знакомую форму колоколообразной кривой, но здесь важно использовать термины «нормальное» или «гауссово», а не «колоколообразная кривая», потому что и другие типы распределений имеют аналогичную форму. Многочисленные явления, изучаемые в технических, физических и социальных науках, при статистическом анализе дают нормальное распределение.
Характеристики нормального распределения
Нормальное распределение – это математически определенная взаимосвязь, которая описывает значения в наборе данных, а реальные измерения аппроксимируют эту взаимосвязь по мере увеличения размера выборки. Давайте посмотрим на некоторые важные особенности нормального распределения.
- Общий вид распределения получается путем построения функции \(e^{-x^2}\).
- Конкретная форма заданного нормального распределения полностью определяется средним значением и стандартным отклонением. Другими словами, если вы знаете среднее значение и стандартное отклонение для нормально распределенного набора данных, вы можете построить форму гистограммы.
- Среднее значение определяет, где будет центр кривой, а стандартное отклонение определяет ее видимую ширину. В приведенном выше распределении среднее значение равно 0, а стандартное отклонение равно 5.
- Хотя теоретически кривая Гаусса простирается до положительной и отрицательной бесконечностей, ожидаемое количество появлений становится чрезвычайно малым, когда значения более чем примерно на 3 стандартных отклонения выше или ниже среднего значения.
Гистограммы и функции плотности вероятности
Если мы соберем большое количество данных для переменной, которая следует нормальному распределению, мы можем представить эти данные в виде гистограммы, и эта гистограмма будет иметь форму кривой Гаусса. С другой стороны, если мы знаем среднее значение и стандартное отклонение данных, мы можем нарисовать функцию плотности вероятности, которая соответствует нашим эмпирическим наблюдениям.
Для этого воспользуемся следующей формулой:
\[P(x)=\frac{1}{\sqrt{2\pi}\sigma}e^{\frac{-(x-\mu)^2}{2\sigma^2}}\]
где μ – среднее значение, а σ – стандартное отклонение.
Ниже показан график функции плотности вероятности нормально распределенной переменной со средним значением 0 и стандартным отклонением равно 5.
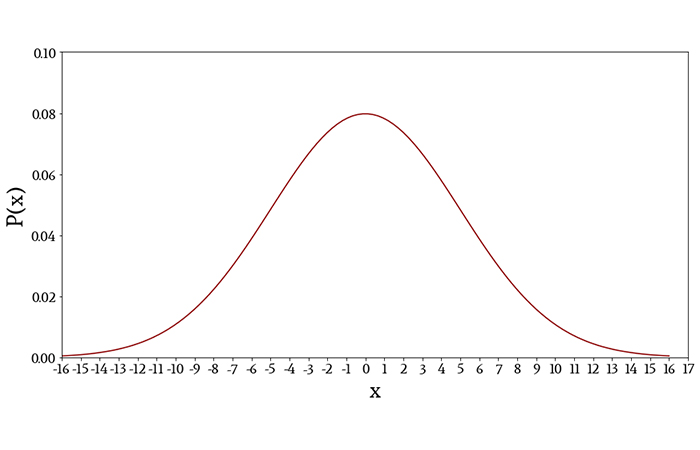
Интерпретация функции плотности вероятности
Вычисляя площадь под кривой P(x) в заданном интервале (скажем, от –3 до +3), мы определяем вероятность того, что результат случайно выбранного измерения попадет в этот интервал.
Для практических целей мы можем интерпретировать P(x) как вероятность того, что результат случайно выбранного измерения будет приблизительно равен определенному значению.
Например, предположим, что функция плотности вероятности, показанная выше, соответствует гистограмме, которую мы сгенерировали путем измерения напряжения сигнала датчика (в милливольтах). Все значения были округлены до ближайшего милливольта. Среднее значение составило 0 В, а стандартное отклонение было равно 5 мВ.
Мы рассчитали гауссово значение P(x), используя приведенную выше формулу, и построили график P(x), чтобы получить кривую, которая является непрерывным математическим представлением распределения измеренных напряжений датчика. Теперь мы смотрим на график и видим, что значение 6 мВ соответствует P(x) = 0,04, что указывает на то, что существует 4%-ная вероятность того, что случайно выбранное измерение напряжения даст в результате приблизительно 6 мВ.
Я считаю полезным думать о функции плотности вероятности таким образом, но помните, что эта интерпретация неверна со строго математической точки зрения. Функция плотности вероятности является непрерывной, и, следовательно, вероятность отлична от нуля только в интервале, а не в одном точном значении на горизонтальной оси.
Нормализация функции плотности вероятности.
Все функции плотности вероятности нормализованы, поэтому полная площадь под кривой равна 1.
Это имеет смысл: площадь под всей кривой дает нам вероятность того, что результат случайно выбранного измерения попадет в интервал, соответствующий всей кривой. Поскольку существует 100%-ная вероятность того, что значение будет где-то в этом интервале, результат интегрирования P(x) должен быть равен 1.
Из-за этой нормализации, если мы построим P(x) и гистограмму на одних и тех же осях, они не будут совпадать: P(x) простирается по вертикальной оси только от 0 до 0,08, тогда как гистограмма простирается от 0 до 8000 (поскольку она была создана с использованием 100000 точек данных).
Однако если я умножу P(x) на 100000 и добавлю полученную кривую на диаграмму гистограммы, вы увидите, что функция плотности вероятности Гаусса математически совпадает с измеренным распределением.
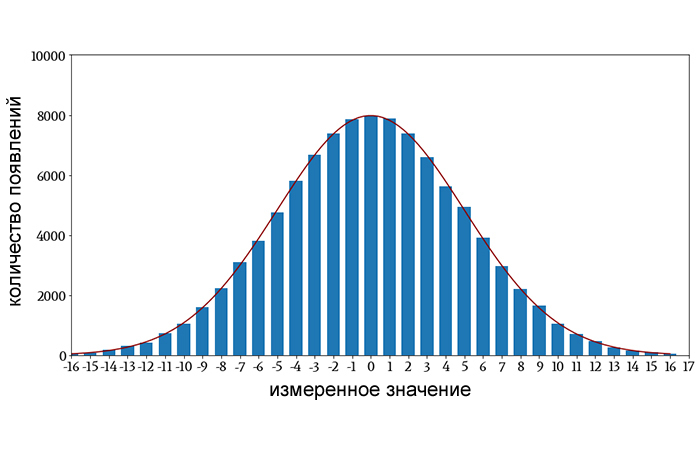
Заключение
Надеюсь, вам понравилась эта статья и то, что нормальное распределение в ней представлено с хорошим балансом практических и теоретических соображений. Мы продолжим обсуждение нормального распределения в следующей статье.
