Среднее отклонение, стандартное отклонение и дисперсия в обработке сигналов
В данной статье рассматриваются три описательных статистических меры с точки зрения приложений обработки сигналов.
В предыдущей статье, посвященной описательной статистике для инженеров-электронщиков, мы увидели, что центральную тенденцию набора данных могут передавать как среднее арифметическое, так и медиана. Несмотря на то, что медиана менее чувствительна к выбросам, в электронике и цифровой обработке сигналов чаще используется среднее арифметическое. Среднее арифметическое, по сути, является основным статистическим методом в электротехнике.
Однако для адекватного описания или понимания набора данных нам часто требуется нечто большее, чем только среднее арифметическое.
Когда мы сообщаем только о центральной тенденции, мы не учитываем важный аспект данных, а именно то, каким образом значения отклоняются от центральной тенденции.
Отклонение от среднего значения
Давайте представим, что мы оцифровали два аналоговых входных сигнала. Если мы преобразуем цифровые коды обратно в единицы вольт и построим графики по времени, они будут выглядеть следующим образом:
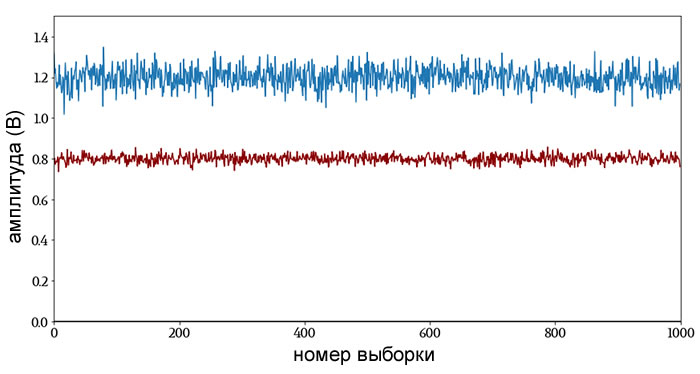
Мы можем довольно хорошо угадать средние значения, просто взглянув на график: центральная тенденция синего сигнала равна 1,2 В, а красного сигнала – 0,8 В. Но если мы сообщим только о средних значениях, мы создадим впечатление, что единственное важное различие между этими двумя сигналами – это разница средних значений 0,4 В (или мы можем назвать это уровнем постоянной составляющей или смещением по постоянному напряжению). Очевидно, что это еще не всё.
Инженер-электронщик интуитивно идентифицирует эти сигналы как устойчивые сигналы постоянного напряжения (возможно, напряжения питания), которые содержат довольно много шума.
Что еще более важно, мы немедленно признаем, что синий сигнал значительно более шумный, чем красный сигнал. Это основное различие в шумовых характеристиках теряется, если рассматривать только среднее значение.
Кстати, почему мы замечаем шум в этих сигналах? Так как
- отдельные значения заметно отклоняются от среднего значения,
- они делают это так, что кажутся случайными, и
- отклонения малы относительно среднего значения.
Когда статистик видит небольшие случайные отклонения от среднего значения, инженер-электронщик видит шум.
Среднее отклонение
Насколько шумные эти сигналы? Довольно шумные? Очень шумные? Попробуем дать более точный ответ на этот вопрос. Другими словами, нам нужно количественно определить отклонение в этих наборах данных.
Моя первая мысль при измерении отклонения состоит в том, чтобы найти расстояние между каждой точкой данных и средним значением, а затем вычислить среднее значение всех этих расстояний. Это даст нам среднее отклонение (также называемое средним абсолютным отклонением, MAD, mean absolute deviation), то есть типовое значение, на которое значения отклоняются от центральной тенденции. Ниже показана формула среднего отклонения:
\[\text{среднее отклонение}=\frac{1}{N}\sum_{k=0}^{N-1}|x[k]-\mu|\]
где N – количество значений в наборе данных, μ – среднее значение, а x[k] – сигнал, представленный как функция дискретной по времени переменной k.
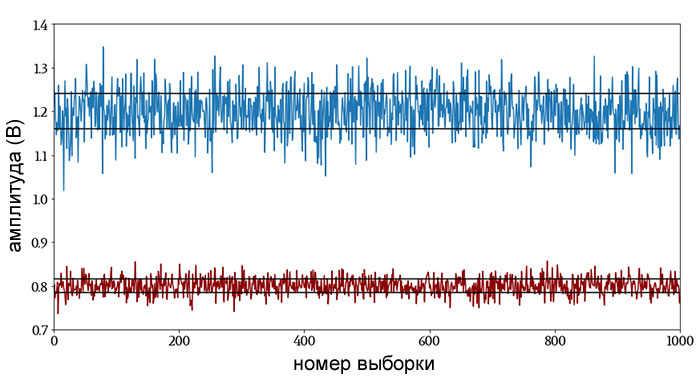
Хотя среднее отклонение интуитивно понятно, оно не является самым распространенным методом количественной оценки склонности сигнала отклоняться от среднего значения. Для этого нам нужно стандартное отклонение.
Дисперсия и стандартное отклонение
В области электротехники проблема со средним отклонением состоит в том, что мы усредняем разности напряжений (или токов), и, следовательно, работаем в области амплитуд. Природа шумовых явлений такова, что при анализе шума мы делаем упор на мощности, а не на амплитуды, и, следовательно, нам нужен статистический метод, который работает в области мощностей.
К счастью, это просто. Мощность пропорциональна квадрату напряжения или тока, и, следовательно, всё, что нам нужно сделать, это возвести разность в квадрат до суммирования и усреднения. Результатом этой процедуры является статистическая мера, называемая дисперсией, обозначаемая σ2 (сигма в квадрате):
\[\sigma^2=\frac{1}{N-1}\sum_{k=0}^{N-1}(x[k]-\mu)^2\]
Мы можем описать дисперсию как усредненную мощность случайных отклонений сигнала, выраженную в виде мощности. Это означает, что единица измерения дисперсии будет отличаться единицы измерения значений, с которых мы начинали. Если мы анализируем колебания в сигнале напряжения, дисперсия имеет единицы измерения В2 вместо В.
Если мы хотим выразить склонность сигнала отклоняться случайным образом, используя исходную единицу измерения, мы должны компенсировать возведение в квадрат каждой разности, применив к конечному значению квадратный корень:
\[\sigma=\sqrt{\sigma^2}=\sqrt{\frac{1}{N-1}\sum_{k=0}^{N-1}(x[k]-\mu)^2}\]
Эта процедура генерирует статистическую меру, известную как стандартное отклонение, то есть усредненную мощность случайных отклонений сигнала, выраженную в виде амплитуды. Таким образом, если мы анализируем сигнал напряжения, стандартное отклонение имеет единицы измерения В, несмотря на то, что мы вычислили стандартное отклонение, используя квадрат отклонений напряжения.
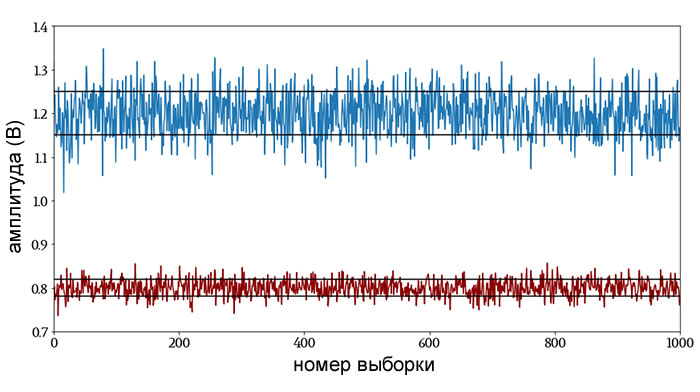
Дисперсия и стандартное отклонение по-разному выражают одну и ту же информацию. Хотя дисперсия, насколько я понимаю, более удобна в определенных аналитических ситуациях, стандартное отклонение обычно предпочтительнее, поскольку это число, которое можно непосредственно интерпретировать, как меру склонности сигнала отклоняться от среднего значения.
Заключение
Стандартное отклонение и дисперсия являются важными статистическими методами, которые часто фигурируют в технических и общественных науках. Я надеюсь, что данная статья помогла вам понять основную связь между этими понятиями и электрическими сигналами, и в следующей статье мы рассмотрим некоторые интересные подробности, связанные со стандартным отклонением.
