Анализ неисправностей компонентов (продолжение)

Я считаю, что понимаю уравнение, когда могу предсказать свойства его решений, не решая его.

В этой цитате Дирака много правды. С небольшими изменениями я могу распространить ее мудрость на электрические схемы, сказав: «Я считаю, что понимаю схему, когда могу предсказать приблизительные эффекты различных изменений, внесенных в нее, без реального выполнения каких-либо вычислений».

В конце главы, посвященной последовательным и параллельным цепям, мы кратко рассмотрели, как цепи могут быть проанализированы качественным, а не количественным образом. Развитие этого навыка – важный шаг на пути к тому, чтобы стать опытным специалистом в устранении неисправностей электрических цепей. Как только вы получите полное представление о том, как конкретная неисправность повлияет на схему (т.е. вам не нужно выполнять какие-либо арифметические действия, чтобы предсказать результаты), будет намного проще работать в обратном направлении: определить источник неполадки с помощью оценки поведения схемы.

Также в конце главы, посвященной последовательным и параллельным цепям, было показано, что табличный метод работает так же хорошо, как при анализе неисправностей, так и при анализе исправных цепей. Мы можем пойти дальше в этой методике и адаптировать ее для полного качественного анализа. Под «качественным» я подразумеваю работу с символами, представляющими «увеличение», «уменьшение» и «без изменений», вместо точных числовых значений.

Мы всё еще можем использовать принципы последовательных и параллельных цепей и концепции закона Ома. Мы просто будем использовать символические качества вместо числовых величин (количеств). Поступая так, мы можем добиться более интуитивного понимания того, как работают схемы, вместо того, чтобы полагаться на абстрактные уравнения, достигая определения «понимания» Дирака.

Анализ неисправностей компонентов сложных схем

Хватит разговоров. Давайте попробуем эту методику на примере реальной схемы и посмотрим, как она работает:

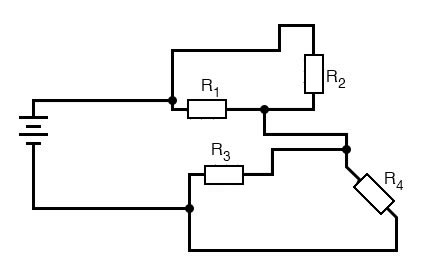
Это первая «запутанная» схема, которую мы «выпрямили» при анализе в предыдущем разделе. Поскольку вы уже знаете, как эта конкретная схема сводится к последовательным и параллельным участкам, я пропущу этот процесс и сразу перейду к окончательной форме:

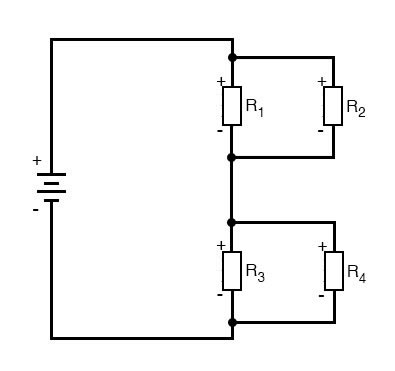
R₃ и R₄ параллельны друг другу; так же R₁ и R₂. Параллельные эквиваленты R₃||R₄ и R₁||R₂ включены последовательно друг с другом. Выраженное в символической форме, полное сопротивление для этой цепи выглядит следующим образом:

R_общ= (R₁||R₂)—(R₃||R₄)

Примечание. Символ «—» здесь используется для обозначения последовательного соединения, так же как символ «||» используется для обозначения параллельного соединения.

Для начала нам нужно сформировать таблицу со всеми необходимыми строками и столбцами для этой схемы:

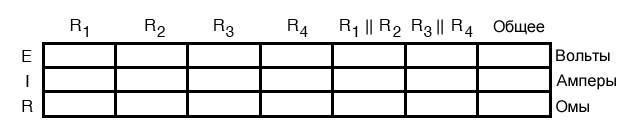
Анализ неисправности

Далее нам нужен сценарий неисправности. Предположим, что резистор R₂ должен был замкнуться накоротко. Предположим, что все остальные компоненты сохраняют свои исходные значения. Поскольку мы будем анализировать эту схему скорее качественно, чем количественно, мы не будем добавлять в таблицу какие-либо реальные числа.

Для любой величины, не изменившейся после отказа компонента, мы будем использовать фразу «не изм.» (не изменилось), чтобы обозначить «без изменений по сравнению с предыдущим значением». Для любой величины, которая изменилась в результате сбоя, мы будем использовать стрелку вниз для «уменьшилась» и стрелку вверх для «увеличилась».

Как обычно, мы начинаем с заполнения полей таблицы для отдельных сопротивлений и общего напряжения нашими «заданными» значениями:

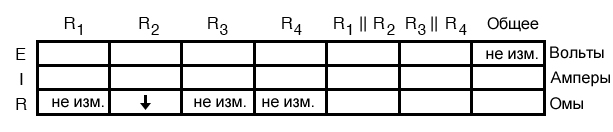
Единственное «заданное» значение, отличное от нормального состояния цепи, – это R₂, которое, как мы сказали, было создает короткое замыкание из-за неисправности (аномально низкое сопротивление). Все остальные начальные значения такие же, как и раньше, и представлены записями «не изм.». Всё, что нам нужно сейчас сделать, это применить знакомые закон Ома и принципы последовательно-параллельных цепей, чтобы определить, что произойдет со всеми другими значениями схемы.

Во-первых, нам нужно определить, что происходит с сопротивлениями параллельных участков R₁||R2 и R₃||R₄. Если ни R₃, ни R₄ не изменили значение сопротивления, то их параллельная комбинация тоже не изменится.

Однако, поскольку сопротивление R₂ уменьшилось, а R₁ осталось прежним, сопротивление их параллельной комбинации также должно уменьшиться:

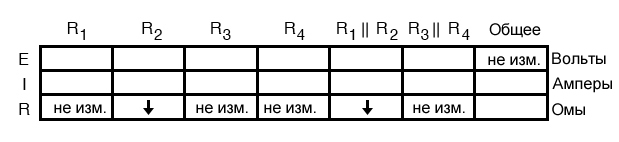
Теперь нам нужно выяснить, что происходит с общим сопротивлением. Это просто: когда мы имеем дело с заменой только одного компонента в цепи, изменение общего сопротивления будет происходить в том же направлении, что и изменение вышедшего из строя компонента. Это не означает, что величина между изменением отдельного компонента и изменением всей цепи будет одинаковой, это просто направление изменения. Другими словами, если значение какого-либо отдельного резистора уменьшается, общее сопротивление цепи также должно уменьшаться, и наоборот.

В этом случае, поскольку R₂ – единственный вышедший из строя компонент, и его сопротивление уменьшилось, общее сопротивление должно уменьшиться:

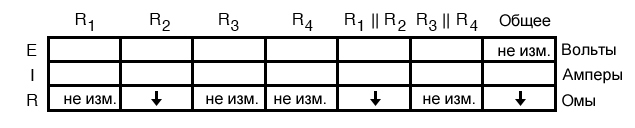
Теперь мы можем применить закон Ома (качественно) к столбцу «Общее». Учитывая тот факт, что общее напряжение осталось прежним, а общее сопротивление уменьшилось, мы можем сделать вывод, что общий ток должен увеличиться (I = E/R).

Использование качественной оценки закона Ома в анализе неисправностей

Если вы не знакомы с качественной оценкой уравнений, то она работает следующим образом. Сначала мы записываем уравнение как решенное для неизвестной величины. В этом случае мы пытаемся найти силу тока через заданные напряжение и сопротивление:

\[I = \frac{E}{R}\]

Теперь, когда наше уравнение представлено в правильном виде, мы оцениваем, какое изменение (если оно есть) испытает «I», учитывая изменение(я) «E» и «R»:

\[I = \frac{E \ \text{(не изм.)}}{R \ \downarrow}\]

Если знаменатель дроби уменьшается, а числитель остается прежним, то общее значение дроби должно увеличиться:

\[\uparrow \ I = \frac{E \ \text{(не изм.)}}{R \ \downarrow}\]

Следовательно, закон Ома (I = E/R) говорит нам, что ток (I) будет увеличиваться. Отмечаем это в нашей таблице стрелкой «вверх»:

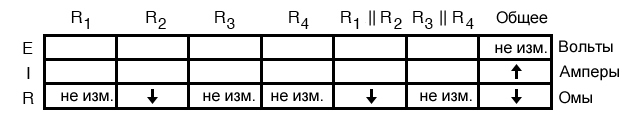
После заполнения всех ячеек сопротивлений в таблице и определения всех значений в столбце «Общее» мы можем перейти к определению других напряжений и токов. Зная, что полное сопротивление в этой таблице было результатом последовательного включения R₁||R₂ и R₃||R₄, мы знаем, что значение общего тока будет таким же, как и в R₁||R₂ и R₃||R₄ (потому что через последовательные компоненты течет один и тот же ток).

Следовательно, если общий ток увеличился, то ток через R₁||R₂ и R₃||R₄ при выходе из строя R₂ также должен увеличиться:

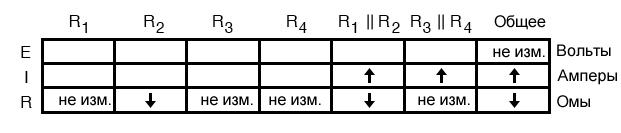
По сути, то, что мы делаем здесь с качественным использованием закона Ома и правил последовательных и параллельных цепей, не отличается от того, что мы делали раньше с числовыми значениями. На самом деле это намного проще, потому что вам не нужно беспокоиться о том, что при вычислении будет допущена арифметическая ошибка или ошибка в нажатии клавиши калькулятора. Вместо этого вы просто сосредотачиваетесь на принципах, лежащих в основе формул.

Из нашей таблицы выше видно, что к столбцам R₁||R₂ и R₃||R₄ должен применяться закон Ома. Для R₃||R₄ мы вычисляем, что происходит с напряжением при увеличении тока и отсутствии изменения сопротивления. Интуитивно мы видим, что это должно привести к увеличению напряжения на параллельной комбинации R₃||R₄:

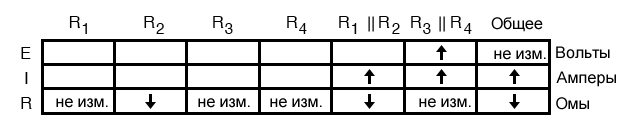
Использование правил анализа цепей при анализе неисправностей

Но как применить ту же формулу закона Ома (E = IR) к столбцу R₁||R₂, где сопротивление уменьшается, и ток увеличивается? Просто определить, изменяется ли только одна переменная, как это было с R₃||R₄, но если изменяются две переменные, и нет определенных чисел, с которыми можно было бы работать, закон Ома не сильно поможет.

Однако есть еще одно правило, которое мы можем применить по горизонтали, чтобы определить, что происходит с напряжением на R₁||R₂: правило для напряжения в последовательных цепях. Если напряжения на R₁||R₂ и R₃||R₄ в сумме равны общему напряжению (батареи), и мы знаем, что напряжение на R₃||R₄ увеличилось, а общее напряжение осталось прежним, тогда напряжение на R₁||R₂должно уменьшиться при изменении значения сопротивления R₂:

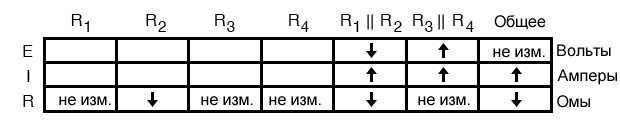
Теперь мы готовы перейти к новым столбцам в таблице. Зная, что R₃ и R₄ составляют параллельный участок R₃||R₄, и, что напряжение на параллельных компонентах одинаковое, увеличение напряжения, наблюдаемое на параллельной комбинации R₃||R₄, также должно наблюдаться на R₃ и R₄ по отдельности:

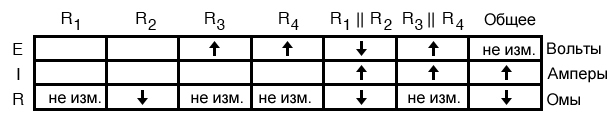
То же самое касается R₁ и R₂. Снижение напряжения, наблюдаемое на параллельной комбинации R₁ и R₂, будет видно на R₁ и R₂ по отдельности:

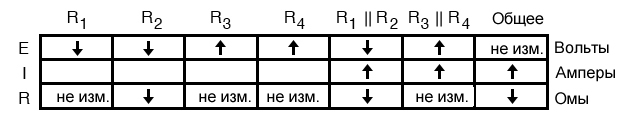
Применяя закон Ома по вертикали к этим столбцам с неизменными значениями сопротивления, мы можем сказать, что будет происходить с током через эти компоненты. Повышенное напряжение на неизменном сопротивлении приводит к увеличению тока. И наоборот, уменьшение напряжения на неизменном сопротивлении приводит к уменьшению тока:

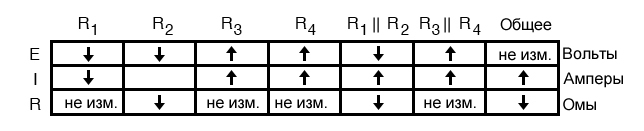
И снова мы оказываемся в ситуации, когда закон Ома не может нам помочь: для R₂ уменьшились и напряжение, и сопротивление, но, не зная, насколько сильно изменилось каждое из них, мы не можем использовать формулу I = E/R, чтобы качественно определить результирующее изменение тока. Тем не менее, мы по-прежнему можем применять по горизонтали правила последовательных и параллельных цепей. Мы знаем, что ток через параллельную комбинацию R₁||R₂ увеличился, и мы также знаем, что ток через R₁ уменьшился.

Одно из правил параллельных цепей – полный ток равен сумме токов отдельных ветвей. В этом случае ток через R₁||R₂ равен току через R₁ плюс ток через R₂. Если ток через R₁||R₂ увеличился, а ток через R₁ уменьшился, ток через R₂должен увеличиться:

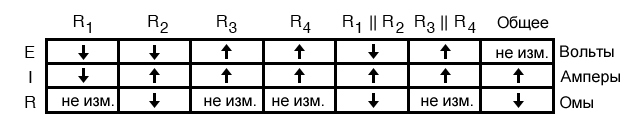
На этом наша таблица качественных оценок завершена. Это конкретное упражнение может показаться трудоемким из-за подробных комментариев, но реальный процесс при некоторой практике может быть выполнен очень быстро. Здесь важно понимать, что общая процедура мало отличается от количественного анализа: начните с известных значений, затем перейдите к определению общего сопротивления, затем общего тока, затем перенесите значения напряжения и тока в соответствии с правилами последовательных и параллельных цепей в соответствующие столбцы.

Можно запомнить несколько общих правил, которые помогут и/или будут контролировать ваш прогресс при проведении такого анализа:

• При одиночной неисправности любого компонента (обрыв или короткое замыкание) общее сопротивление всегда будет изменяться в том же направлении (увеличиваться или уменьшаться), что и изменение сопротивления отказавшего компонента.
• Когда компонент выходит из строя с коротким замыканием, его сопротивление всегда уменьшается. Кроме того, ток через него увеличится, а напряжение на нем может упасть. Я говорю «может», потому что в некоторых случаях он останется прежним (пример: простая параллельная цепь с идеальным источником питания).
• Когда компонент выходит из строя с обрывом, его сопротивление всегда увеличивается. Ток через этот компонент снизится до нуля, потому что он будет представлять собой неполный электрический путь (отсутствие непрерывности). Это может привести к увеличению напряжения на нем. То же самое исключение, указанное выше, применимо и здесь: в простой параллельной цепи с идеальным источником напряжения напряжение на отказавшем компоненте с обрывом останется неизменным.

Теги