Определение статистической значимости из t-тестов, применяемых к инженерным системам
В данной статье обсуждаются важные аспекты t-тестирования с помощью примера эксперимента, представленного в предыдущей статье.
Добро пожаловать в серию статей о статистике в электротехнике. Ближе к концу серии вы можете задаться вопросом о базовых строительных блоках, которые ведут к этому моменту. Если вы хотите наверстать упущенное, просмотрите список предыдущих статей в оглавлении выше. В противном случае перейдите к следующему разделу, чтобы узнать больше о том, как мы можем получить статистическую значимость из t-тестов, применяемых к инженерным системам.
Обзор наших расчетных t-значений
Как было описано в предыдущей статье, в ходе нашего воображаемого эксперимента мы получили следующие результаты измерений, касающиеся рабочей температуры и коэффициента пакетных ошибок (PER):
| PER |
|---|
| 0,0010290 |
| 0,0010113 |
| 0,0010380 |
| 0,0010198 |
| 0,0009702 |
| 0,0010486 |
| 0,0010503 |
| 0,0009941 |
| 0,0010067 |
После вычисления выборочного среднего и выборочного стандартного отклонения мы определили, что t = 2,13. Поскольку критическое значение было t* = 1,86, мы обнаружили, что t > t*, и, следовательно, мы отвергли нулевую гипотезу.
Одностороннее и двустороннее тестирование
Одним из сомнительных аспектов нашего эксперимента было предположение, что повышение температуры приведет только к равной или худшей производительности относительно PER. Из-за этого предположения наш анализ не рассматривал возможность корреляции более высокой температуры с улучшением PER, и это было отражено в использовании одностороннего теста:
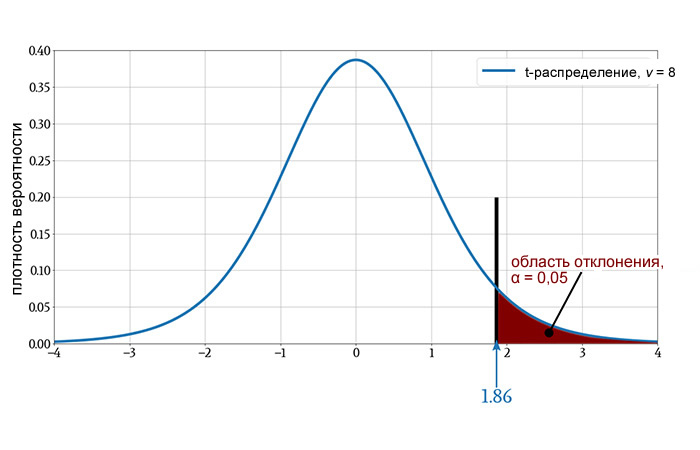
Верно ли это предположение? Температуры, которые значительно превышают комнатную температуру, приводят к тому, что электронные схемы ведут себя не так, как хотелось бы.
Однако на взаимосвязь между температурой и производительностью системы влияют различные факторы, которые взаимодействуют потенциально сложным образом. Кроме того, наш пример построен на системе беспроводной связи, и поведение радиочастотной схемы особенно трудно предсказать.
Таким образом, мы можем решить спланировать эксперимент иначе. Поскольку мы беремся за нагрев лаборатории, настройку системы, сбор данных и т.д., возможно, имеет смысл поискать доказательства того, что повышение температуры может вызвать статистически значимое изменение PER.
Мы больше не ищем просто ухудшение PER. Теперь мы предполагаем, что повышенная рабочая температура может привести к более высокому или более низкому PER, а это означает, что нам нужен двусторонний тест.
Двусторонний тест с таким же уровнем значимости имеет такое же количество вероятностной массы в области отклонения, но эта область разделена на две части: одна выше среднего, а другая ниже среднего. Следовательно, критическое значение изменится:
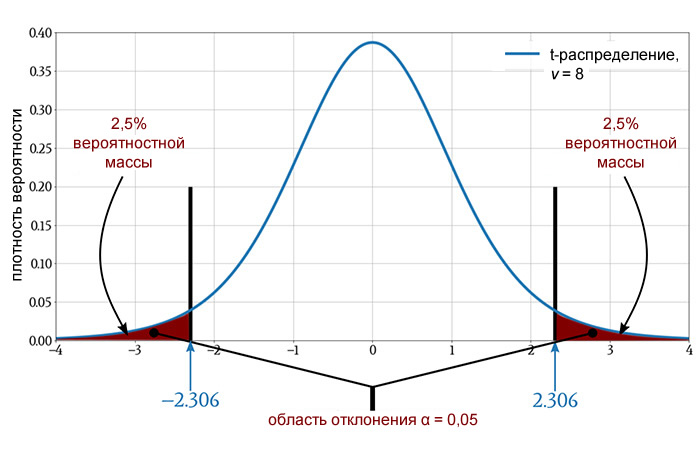
Произошло кое-что интересное: наше t-значение 2,13 не превышает критического значения! Другими словами, наш анализ теперь показывает, что эксперимент не продемонстрировал взаимосвязи между температурой и PER.
Этот пример заставляет задуматься о двух вещах. Во-первых, нам нужно быть осторожными с предположениями, которые приводят нас к одностороннему или двустороннему тесту, потому что эти предположения могут быть определяющими факторами в нашей оценке статистической значимости.
Во-вторых, проверка значимости не является надежной чисто математической процедурой. Помимо выбора одностороннего или двустороннего тестирования, у нас есть сам порог значимости, который является довольно произвольным. Верно, что двусторонний тест переместил t-значение из области отклонения, но мы могли бы переместить его обратно в область отклонения, выбрав ⍺ = 0,1 вместо ⍺ = 0,05.
Влияние размера выборки на статистическую значимость
Отказ от нулевой гипотезы происходит, когда t-значение больше критического значения. Таким образом, если наша цель – продемонстрировать статистическую значимость, нам нужно более высокое t-значение. Давайте еще раз посмотрим на уравнение, которое мы используем для вычисления t-значений:
\[t=\frac{\bar{x}-\mu}{s/\sqrt{n}}\]
Если мы увеличиваем размер выборки (обозначается, как n), величина \(s/ \sqrt{n}\) уменьшается, а это вызывает увеличение t-значения. Таким образом, если мы хотим получить более высокое t-значение, всё, что нам нужно сделать, это увеличить размер выборки.
Например: если я возьму точно те же самые результаты измерений PER, но скопирую набор данных пять раз (и поэтому размер выборки станет n = 54), t-значение увеличится с исходного t = 2,13 до t = 5,48. Если мы собираем больше данных, мы увеличиваем t-значение, даже если новые измерения не приводят к заметным изменениям среднего или стандартного отклонения.
Что еще хуже, с увеличением размера выборки уменьшается критическое значение. При n = 9 было ν = 8 и t* = 1,860. При n = 54 мы имеем ν = 53 и t* = 1,674. В целом, большие размеры выборки облегчают достижение статистической значимости, поскольку они, как правило, приводят к более высоким t-значениям и более низким критическим значениям.
Это известная проблема статистического анализа, в котором мы вычисляем p-значение и сравниваем его с уровнем значимости. Вы можете узнать больше об этом в статье, озаглавленной «Using Effect Size—or Why the P Value Is Not Enough». В этой статье указывается, что очень большой размер выборки может привести к статистически значимому p-значению, даже если реальный эффект незначителен.
Заключение
Надеюсь, что эта статья и предыдущая статья помогли вам понять, как t-тест может быть полезен при определении характеристик или устранении неисправностей в электронной системе. Также хорошо бы помнить, что статистическая значимость имеет свои ограничения.
Возможно, в следующей статье мы обсудим размер эффекта, на который не влияет размер выборки, и функции, которые являются важным дополнением к статистической значимости.
