Компенсация размера выборки в расчетах стандартного отклонения
В данной статье обсуждается коррекция Бесселя, которая помогает нам более точно оценить стандартное отклонение определенных параметров и сигналов большой длительности.
Данная статья продолжает нашу серию статей о статистике для инженеров-электронщиков, первая из которых представляет статистику как средство анализа поведения цепей и описания характеристик инженерных систем. Затем мы обсудили конкретные методы, в частности, использование среднего арифметического и медианы для определения центральной тенденции набора данных.
Совсем недавно мы коснулись трех показателей описательной статистики (среднего отклонения, стандартного отклонения и дисперсии в обработке сигналов), чтобы разобраться с отклонениями от этих центральных тенденций.
На фоне нашей последней статьи о стандартном отклонении мы можем рассмотреть еще один ключевой аспект этой темы: компенсацию размера выборки в расчетах стандартного отклонения.
Делить на N или на N–1?
Если вы читали предыдущую статью, то, возможно, заметили явное несоответствие в формуле, которую мы используем при расчете стандартного отклонения дискретных данных. Формула выглядела следующим образом:
\[\sigma=\sqrt{\sigma^2}=\sqrt{\frac{1}{N-1}\sum_{k=0}^{N-1}(x[k]-\mu)^2}\]
Стандартное отклонение передает усредненную мощность случайных отклонений сигнала. Однако, когда мы вычисляем среднее (то есть среднее арифметическое) чего-либо, мы всегда делим на N (где N обозначает количество точек данных), а не на N–1.
Почему мы используем N–1 при расчете стандартного отклонения?
На самом деле, мы не всегда делим на N–1. Мы можем вычислить стандартное отклонение, используя N вместо N – 1, но теоретически полученное значение будет представлять собой нечто иное. Я подчеркиваю «теоретически», потому что в контексте электротехники, разница часто будет незначительной. Тем не менее, важно понимать основную концепцию, которая основывается на разнице между выборкой и генеральной совокупностью.
Выборка, генеральная совокупность и стандартное отклонение
Допустим, вы покупаете операционный усилитель (назовем его OPA100) и после некоторых экспериментов в лаборатории вы понимаете, что спецификации в техническом описании не дают вам достаточной информации о входном напряжении смещения при рабочих температурах вашего проекта. Чтобы исправить это, вы решили купить 15 операционных усилителей OPA100 (т.е. N = 15), провести измерения и сформировать статистику на основе этой выборки.
Если OPA100 имеет типовое напряжение смещения 1 мВ при соответствующей рабочей температуре, распределение напряжений смещения в 15-компонентной выборке может выглядеть примерно так:
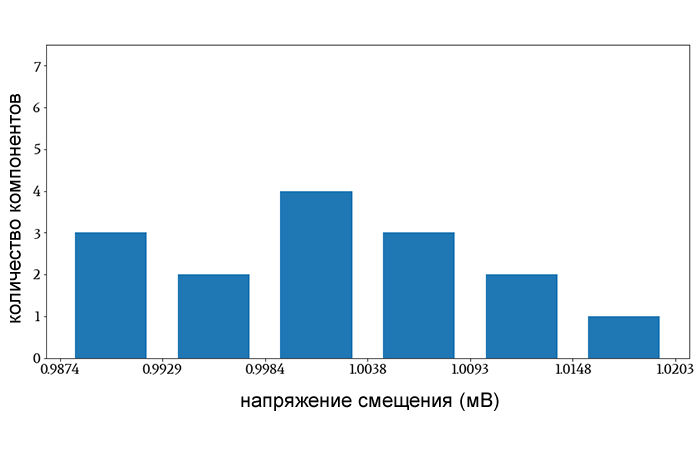
Вы измерили напряжение смещения каждого компонента, и теперь вы можете рассчитать стандартное отклонение, но сначала вам нужно задать себе вопрос: «я хочу рассчитать стандартное отклонение для выборки или для генеральной совокупности?». Другими словами, я должен отчитаться о стандартном отклонении этих 15 компонентов передо мной, или я должен попытаться отчитаться о стандартном отклонении, которое применяется ко всем операционным усилителям OPA100?
Стандартное отклонение выборки
Если мы работаем с выборкой и хотим знать стандартное отклонение выборки, мы делим на N. Это имеет смысл – как упоминалось выше, мы всегда делим на N при вычислении среднего арифметического, а стандартное отклонение включает в себя среднее арифметическое мощности отклонений в наборе данных.
Итак, чтобы продолжить наш пример, деление на N даст вам стандартное отклонение 15 операционных усилителей OPA100, которые вы приобрели.
Другим типом данных, с которым часто сталкиваются инженеры-электронщики, является оцифрованный сигнал напряжения, и, как мы видели в предыдущей статье, стандартное отклонение представляет собой метод количественной оценки электрического шума.
Если вы хотите узнать стандартное отклонение полученного сигнала, то есть конкретные уровни напряжения, которые были оцифрованы и сохранены в памяти, и при расчете стандартного отклонения вы должны делить на N. В этом случае полученный сигнал является статистической выборкой.
Стандартное отклонение генеральной совокупности
Если мы работаем с выборкой и хотим знать стандартное отклонение генеральной совокупности, мы делим на N–1. Термин «генеральная совокупность» относится ко всей группе, для которой предоставленные данные дают репрезентативную выборку. Использование N–1 вместо N – это метод компенсации ошибки, связанной с конечным размером нашей выборки. Этот прием называется коррекцией Бесселя.
Коррекция необходима, потому что если мы хотим рассчитать стандартное отклонение генеральной совокупности, мы должны использовать среднее значение генеральной совокупности. Но обычно к генеральной совокупности у нас доступа нет. У нас есть только среднее значение выборки, которое является приблизительным значением среднего значения генеральной совокупности. Оказывается, что, когда мы используем среднее значение выборки вместо среднего значения генеральной совокупности, рассчитанное стандартное отклонение постоянно получается ниже реального, а деление на N–1 вместо N смягчает этот эффект.
Таким образом, если вы хотите оценить стандартное отклонение напряжения смещения для всех произведенных операционных усилителей OPA100, вам следует собрать данные из вашей 15-компонентной выборки, а затем при расчете стандартного отклонения делить на 14 вместо 15.
Точно так же, если вы хотите количественно оценить шум в напряжении сигнала на основе относительно короткого периода сбора данных, вы должны делить на N–1. В этом случае оцифрованные данные являются выборкой, а сам сигнал является генеральной совокупностью.
Вы также можете думать об этом следующим образом: когда мы делим на N–1, мы фокусируемся на основных процессах, которые создают шум в анализируемом сигнале, а не измеряем влияние этих процессов в течение отрезка времени, представленного полученными точками данных.
Влияние размера выборки
Ваша инженерская интуиция, возможно, говорит вам, что коррекция Бесселя – это не та вещь, которая может решить судьбу вашего анализа, и во многих случаях это правда. В инженерных приложениях у нас часто имеется множество данных, и мы интуитивно понимаем, что эти большие наборы данных будут создавать среднее значение выборки, которое для всех практических целей будет таким же, как среднее для генеральной совокупности. Таким образом, нет необходимости делить на N–1 вместо N.
Однако следует помнить, что связь между делением на N и на N–1 встроена в коррекцию. По мере увеличения N разница между N и N–1 в отношении общего расчета становится менее значимой. Таким образом, использование N–1 применяет необходимую компенсацию, когда такая компенсация требуется (то есть, когда размер выборки мал), и она не оказывает заметного влияния, когда компенсация не требуется (то есть, когда размер выборки велик).
Заключение
Мы увидели, что стандартное отклонение может быть рассчитано по-разному в зависимости от целей анализа и размера выборки. В следующей статье мы рассмотрим взаимосвязь между стандартным отклонением и среднеквадратичными значениями.
