Статистический характер анализа шума: введение
Данная статья представляет собой интуитивное введение в статистическую природу шума и основные расчеты, необходимые для объединения шума от нескольких источников в схеме.
Существуют разные способы описания шума в электрических цепях. Рассмотренный здесь шум – это нежелательный сигнал, исходящий из компонентов схемы. Например, шум Джонсона (тепловой шум) от резисторов или входное шумовое напряжение операционных усилителей.
Данное обсуждение предполагает, что источники шума имеют две характеристики:
- во-первых, несколько источников некоррелированы;
- во-вторых, вероятность определенной амплитуды в определенный момент времени соответствует гауссову или нормальному распределению, которое имеет место для многих источников.
Мы рассмотрим, как представлять шум с помощью наборов данных, среднеквадратичного значения амплитуды источников шума (и как преобразовать эту информацию в размах, в амплитуду пик-пик), и обсудим пример анализа шума в схеме.
Пример набора данных с нормальным распределением
Я скачал набор случайных чисел с сайта с генератором случайных чисел. Это не псевдослучайные числа, а истинные случайные числа, полученные из физического процесса. Здесь 10 000 выборок с гауссовым или нормальным распределением и стандартным отклонением 10. Среднее значение, или центр, распределения равно 0. Ниже приведены первые пять и последние пять чисел последовательности, чтобы вы могли получить представление о диапазоне значений.
| Номер выборки | Значение |
|---|---|
| 1 | -17,6 |
| 2 | -9,63 |
| 3 | 8,26 |
| 4 | 8,44 |
| 5 | -6,65 |
| 9 996 | 14,1 |
| 9 997 | -16,3 |
| 9 998 | -15,2 |
| 9 999 | -0,30 |
| 10 000 | 15,88 |
Для наших целей полезно представлять данные как последовательность выборок во времени, как если бы мы смотрели на осциллограмму шума. Другими словами, обрабатывая данные как шум во временной области. Ниже показаны первые 500 выборок. По-моему, это похоже на шум!
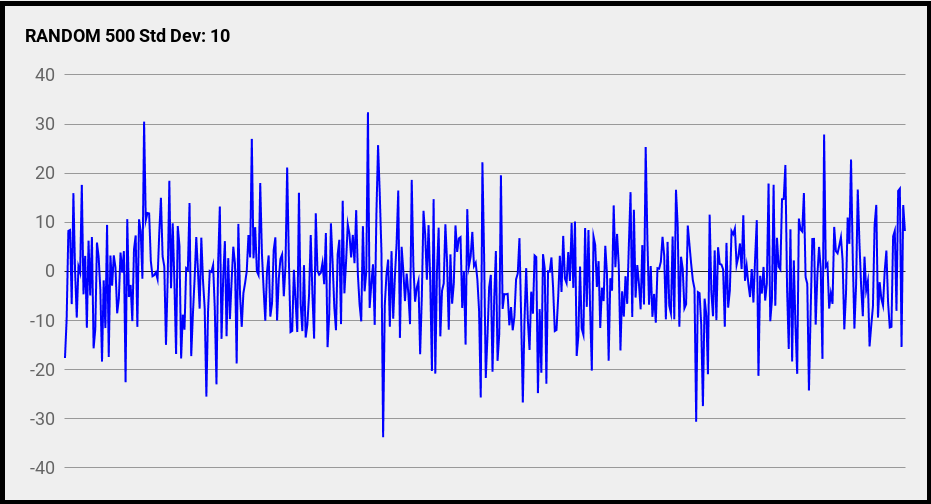
На рисунке ниже все 10000 выборок показаны в виде гистограммы. Это классическое нормальное распределение или кривая в виде «колокола». Я нарисовал линию в центре на значении 0 и линию слева на значении 10, которое равно стандартному отклонению.
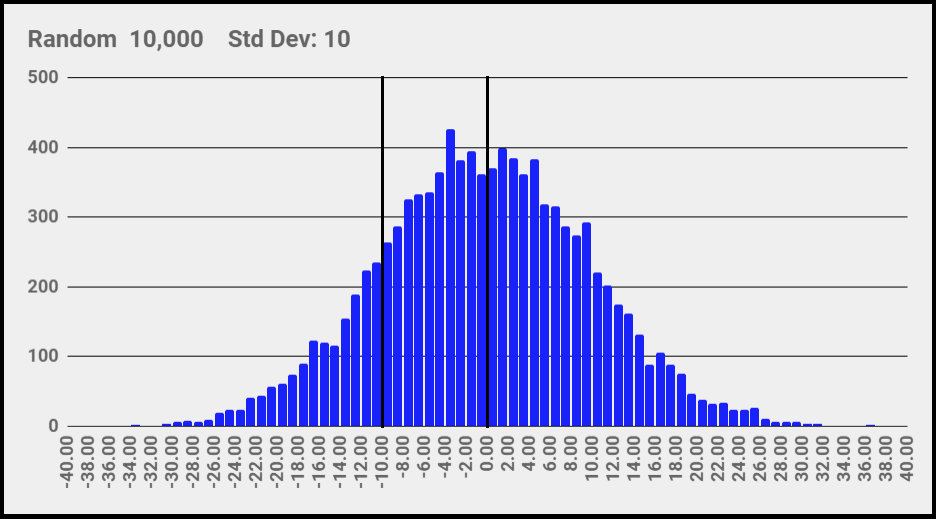
Источники шума и нормальное распределение
Как этот набор данных относится к электронному шуму?
Если источник шума имеет нормальное распределение, среднеквадратичное значение напряжения источника совпадает со стандартным отклонением распределения. На рисунке 1 с графиком из первых 500 выборок среднеквадратичное значение равно стандартному отклонению 10. График из всех 10000 выборок (смотрите рисунок 4 ниже) также будет иметь среднеквадратичное значение 10.
Другая важная связь связана с крайними значениями амплитуды в данных. Самые большие выборки встречаются гораздо реже, чем амплитуды около 0. Об этих «выбросах» будет рассказано в этой же статье подробнее.
Если вы хотите узнать больше о визуализации источников шума, то можете посмотреть статью «Как выполнить анализ переходных процессов и моделирование источника шума с помощью LTspice».
Сложение шума от разных источников
Поскольку источники шума некоррелированы, их амплитуды не складываются арифметически. Другими словами, для двух источников шума, \(V_{общ}≠V_{A}+V_{B}\). Они складываются как квадратный корень из суммы их квадратов; часто это значение упоминается как RSS суммирование (root sum square, корень из суммы квадратов). Например, сумма трех источников шума равна
\[V_{общ} = \sqrt{(V_{A})^2 + (V_{B})^2 + (V_{C})^2}\]
Чтобы было понятнее, из набора данных были взяты три группы из 500 последовательных выборок, чтобы сформировать три, 1 × 500 матриц (векторов). Вектор A из выборок с 1 по 500, B из выборок с 501 по 1000, и C из выборок с 1001 по 1500. Несмотря на то, что группы относятся к одному и тому же набору данных, они некоррелированы. Затем складываем эти три вектора.
\[D = A + B + C\]
Ниже показан график D, на котором показано, как эти три источника в схеме складываются по времени.
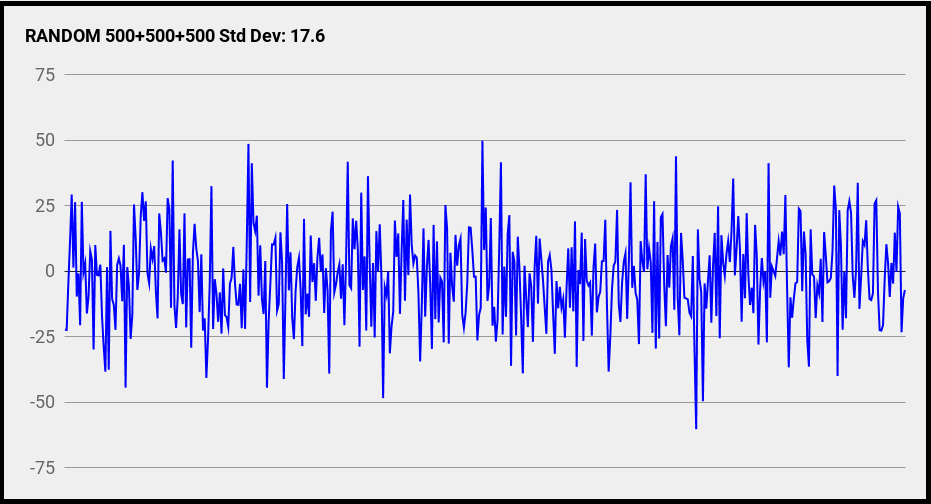
На графике D почти все выборки находятся в пределах ±50. Стандартное отклонение 500 выборок в D составляет 17,6.
Теперь давайте посчитаем сумму среднеквадратичных значений напряжений трех источников.
\[V_{общ} = \sqrt{(V_{A})^2 + (V_{B})^2 + (V_{C})^2}\]
\[V_{общ} = \sqrt{10^2 + 10^2 + 10^2}\]
\[V_{общ} = \sqrt{300}\]
\[V_{общ} = 17,3\]
Мы рассчитали сумму трех источников двумя различными способами. Один рассчитывает сумму как корень из суммы квадратов (RSS) среднеквадратичных значений напряжений трех источников. Другой складывает данные по точкам и определяет стандартное отклонение результата.
\[17,3 ≅ 17,6\]
Довольно близко! Метод среднеквадратичных значений и корня из суммы квадратов полезен, но он не особенно интуитивен. Пример с векторами, напротив, несколько интуитивно понятнее. Мы можем представить некоррелированные источники, изменяющиеся во времени и складывающиеся в схеме.
Сложение двух одинаковых источников шума
Если два источника шума имеют одинаковую амплитуду \(V_{A} = V_{B}\), то общий шум равен
\[V_{общ} = \sqrt{(V_{A})^2 + (V_{B})^2}\]
\[V_{общ} = \sqrt{2\times (V_{A})^2}\]
\[V_{общ} = \sqrt{2}\times V_{A}\]
\[V_{общ} = 1,414\times V_{A}\]
Это соотношение полезно запомнить. Например, эта формула дает общий шум для двух полевых транзисторов на входе дифференциального усилителя.
И наоборот, если общий шум известен, амплитуда одного из источников равна
\[V_{общ} = \sqrt{2}\times V_{A}\]
\[V_{A}=\frac{V_{общ}}{\sqrt{2}}\]
\[V_{A} = 0,707\times V_{общ}\]
Сложение источника с небольшим шумом с источником с большим шумом
Если шум одного источника намного больше шума другого источника, источник меньшего шума часто можно игнорировать. Например, если шум одного источника в 10 раз больше шума другого источника,
\[V_{общ} = \sqrt{(10\times V)^2 + V^2}\]
\[V_{общ} = \sqrt{100\times V^2 + V^2}\]
\[V_{общ} = \sqrt{101\times V^2}\]
\[V_{общ} ≈ 10,05\times V\]
Источник с меньшим шумом добавляет всего 0,5% к общему шуму! Это ничтожно мало в мире шумов или, как говорится, «он поглощен шумом».
Это соотношение объясняет, почему шум в предусилителе важен, а шум в последующих каскадах часто не так важен – шум предусилителя проходит через сильное усиление, а шум, генерируемый последующими каскадами, – нет. Это также бывает полезно, когда мы хотим упростить анализ шума в схеме. Просто отбросьте источники небольшого шума.
Преобразование среднеквадратичного значения в размах (значение пик-пик)
Когда мы работаем с шумом, преобразование среднеквадратичного значения в размах становится немного сложнее. Данное преобразование должно учитывать статистику, и в отличие от преобразования синусоидальных сигналов, оно не использует точное значение.
Ниже показан график из всех 10 000 выборок набора данных.
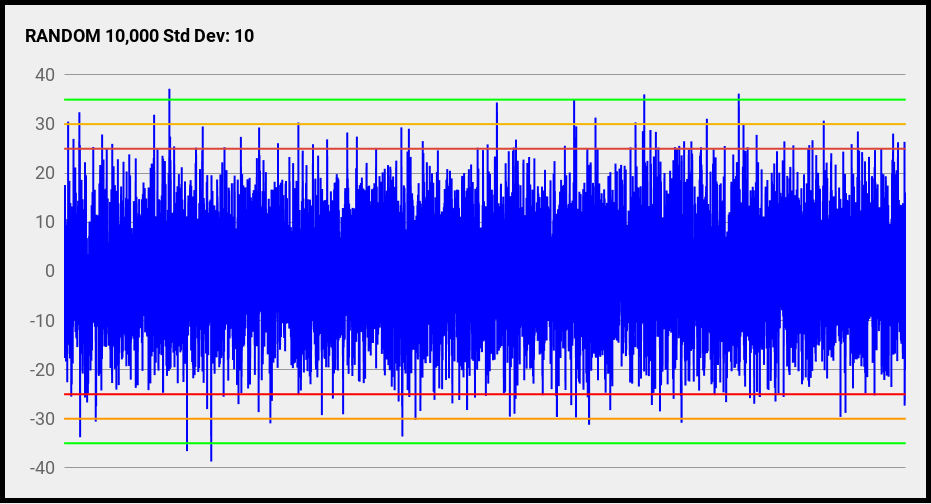
Обратите внимание на крайние положительные и отрицательные пики. Их не очень много.
Кроме того, характер нормального распределения заключается в том, что не существует гарантированных максимальных и минимальных значений. Теоретически, если мы будем ждать достаточно долго, появится еще больший пик.
Таким образом, необходимо сделать предположение о том, где «провести черту», представляющую определение размаха (значения пик-пик). Я добавил на график три набора линий. Они размещаются кратно стандартному отклонению, как показано в таблице ниже.
| Пара линий | x RMS | Диапазон напряжений |
|---|---|---|
| Красная | 5 | ±25 |
| Оранжевая | 6 | ±30 |
| Зеленая | 7 | ±35 |
По-моему, коэффициент, на который мы умножаем значение RMS, зависит от приложения. Выбор коэффициента размаха может быть важен для предотвращения ограничения в усилителе или непревышения порога срабатывания. Для пожарной сигнализации может быть необходим очень большой коэффициент для предотвращения ложных тревог!
Другой способ отобразить среднеквадратичное значение в размах использует нормальное распределение. Ниже показана диаграмма с красными линиями в 5 раз больше среднеквадратичного значения (±25).

Процент выборок за пределами «окна» размаха рассчитывается статистически. К счастью, для этого есть графики и онлайн калькуляторы. Это тема под названием «кумулятивная функция распределения», и может быть сложно, найти подходящий онлайн-калькулятор. Ниже приведена таблица с процентным соотношением точек вне окна или, другими словами, количеством времени, в течение которого шум находится вне окна.
| Пара линий | x RMS | % вне окна |
|---|---|---|
| Красная | 5 | 1,2% |
| Оранжевая | 6 | 0,27% |
| Зеленая | 7 | 0,046% |
6хRMS используется часто. Некоторым нравится коэффициент 6,6, потому что он соответствует 0,10%. Хорошее число, но, на мой взгляд, не более значимое, чем другие, без рассмотрения особенностей приложения. Мне нравится 6,.283185 (≅2π). Я требую использовать его!
Помните, что данные случайны и описываются вероятностями. Невозможно узнать, когда значение шума источника выйдет за это окно. Даже если окно большое, выход за его пределы может произойти в следующую секунду, а может не произойти и в течение недели, или вообще не произойти.
Пример схемы
В данном разделе для анализа предусилителя и определения общего выходного шума используются концепции, приведенные выше. Я использую расчет «точечного шума» для шума на частоте 1 кГц и шириной полосы 1 Гц.
Целью здесь является проверка объединения нескольких источников шума. Ручные расчеты сравниваются с моделированием шума, выполненным с помощью LTspice, популярного и бесплатного симулятора цепей от Analog Devices. Если вы хотите узнать больше об этом процессе, то смотрите статью «Руководство по анализу шума с помощью LTspice».
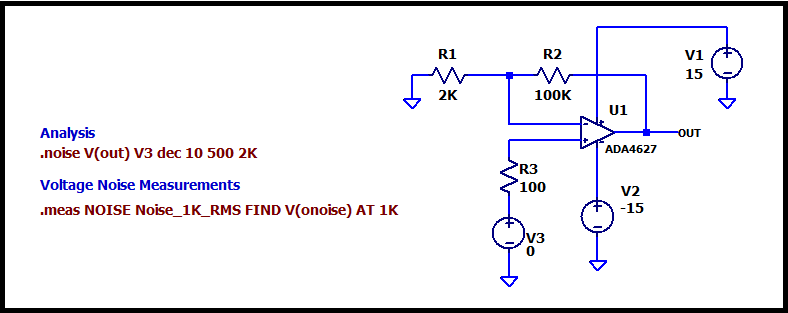
Схема представляет собой неинвертирующий усилитель на операционном усилителе (ADA4627 от Analog Devices) с источником входного сигнала, представленным V3. Сопротивление источника 100 Ом включено последовательно входу. Это имитирует платиновый резистивный датчик температуры (RTD).
Все источники шума перечислены в следующей таблице.
| Источник | Плотность напряжения шума на источнике (В/√Гц@1кГц) | Коэффициент усиления | Плотность напряжения шума на выходе(В/√Гц@1кГц) | Описание |
|---|---|---|---|---|
| R1 | 5,75E-9 | 50 | 287,5E-9 | Тепловой шум (шум Джонсона) |
| R2 | 40,7E-9 | 1 | 40,7E-9 | Тепловой шум (шум Джонсона) |
| R3 | 1,3E-9 | 51 | 65,6E-9 | Тепловой шум (шум Джонсона) |
| U1:VN | 5,04E-9 | 51 | 257,0E-9 | Шум входного напряжения |
| U1:IN+ | 0,22E-12 | 51 | 0,01E-9 | Шум входного тока на неинвертирующем входе через R3 |
| U1:IN- | 4,5E-12 | 50 | 0,22E-9 | Шум входного тока на инвертирующем входе через R1 |
R1, R2 и R3 – это источники теплового шума (шума Джонсона) при 27℃. Шум входного напряжения операционного усилителя и шум входного тока можно найти, запустив специальное моделирование LTspice или проверив спецификации в техническом описании.
Шумы входного тока являются источником на каждом входе операционного усилителя (+ и -). Шум входного тока с инвертирующего входа (-) для получения шума входного напряжения умножается на R1, а шум входного тока с неинвертирующего входа (+) умножается на R3.
Наконец, шум на выходе от каждого источника рассчитывается путем умножения шума каждого источника на соответствующий коэффициент усиления. Все напряжения действующие (RMS). Размахи (напряжения пик-пик) здесь не используются!
Выходные шумы от отдельных источников для получения общего выходного шума объединяются с использованием корня из суммы квадратов (RSS).
\[V_{общ} = \sqrt{287,5нВ^2+40,7нВ^2+65,6нВ^2+257нВ^2+0,01нВ^2+0,22нВ^2}\]
\[V_{общ} = 393,3 \frac{нВ}{\sqrt{Гц}}\]
Выполнение моделирования шума в LTspice дает общий выходной шум \(393,4\ {нВ}/{\sqrt{Гц}}\). Неплохо!
Эффект добавления источника небольшого шума к источнику большого шума проверяется путем сравнения выходного шума только от двух крупнейших источников, R1 и U1:VN, с выходным шумом от всех источников.
\[V_{общ} = \sqrt{287,5нВ^2 + 257нВ^2}\]
\[V_{общ} = 385 \frac{нВ}{\sqrt{Гц}}\]
Результат ниже всего на 2%! По моему опыту, часто бывают источники шума, которые можно игнорировать. В данном случае очевидными являются шум входного тока операционного усилителя, поскольку сопротивления источников невелики, а шумовые токи, протекающие через эти резисторы, очень малы.
Комментарий о моделировании шума. При обучении лучше всего выполнить несколько расчетов вручную. Тем не менее, это утомительно и подвержено ошибкам. Переход на симулятор, такой как LTspice, очень помогает, особенно когда в анализ включена ширина полосы частот шума.
Здесь анализ относительно прост, потому что это расчет точечного шума. Для получения дополнительной информации ознакомьтесь с нашими ресурсами из списка ниже.
Больше информации о шуме
- Основы моделирования схем в LTSpice
- Руководство по LTSpice (средний уровень)
- Руководство по анализу шума с помощью LTspice
- Что такое электрический шум, и откуда он появляется?
- Использование LTspice для измерения шума усилителя
