Кумулятивная функция распределения в нормально распределенных данных

В данной статье объясняется, как получить кумулятивную функцию распределения Гаусса и почему она полезна в статистическом анализе.

Если вы только присоединяетесь к нашему обсуждению статистики в электротехнике, возможно, вам будет интересно сначала просмотреть предыдущие статьи этой серии, список которых можно найти в оглавлении вверху над статьей.

Что мы знаем из предыдущих статей:

• мы можем получить функцию плотности вероятности нормально распределенных результатов измерений, вычислив стандартное отклонение и среднее значение набора данных;
• эта функция плотности вероятности является идеализированным математическим эквивалентом фигуры, которую мы наблюдаем на гистограмме набора данных;
• мы получаем вероятность (т.е. вероятность того, что определенные значения результатов измерений будут иметь место) путем интегрирования функции плотности вероятности по заданному интервалу.

Если участки интегрирования функции плотности вероятности являются ключом к извлечению вероятностей из измеренных данных, можно задаться вопросом о возможности простого интегрирования всей функции и тем самым создания новой функции, которая даст нам прямой доступ к информации о вероятности.

Как оказалось, это стандартный метод статистического анализа, и эта новая функция, которую мы получаем путем интегрирования всей функции плотности вероятности, называется кумулятивной функцией распределения.

Кумулятивная функция нормального распределения

Использование кумулятивной функции распределения (CDF, cumulative distribution function) является особенно хорошей идеей, когда мы работаем с нормально распределенными данными, потому что интегрировать гауссову кривую не так-то просто.

Фактически, чтобы получить кумулятивную функцию распределения кривой Гаусса, даже математики должны прибегнуть к численному интегрированию (функция \(e^{-x^2}\) не имеет первообразной, которая может быть выражена в элементарной форме). Это означает, что кумулятивная функция распределения Гаусса на самом деле представляет собой последовательность дискретных значений, созданных из множества отдельных выборок, взятых вдоль гауссовой кривой.

В эпоху компьютеров мы можем легко обрабатывать огромное количество выборок, и, следовательно, дискретная кумулятивная функция распределения, полученная путем численного интегрирования, может быть вполне адекватной заменой непрерывной функции, полученной посредством символьного интегрирования.

Если мы отложим на графике большое количество значений гауссовой функции распределения, кривая будет выглядеть следующим образом:

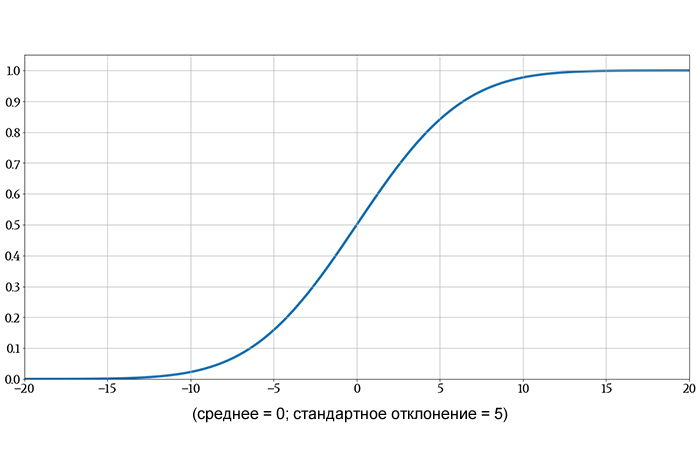
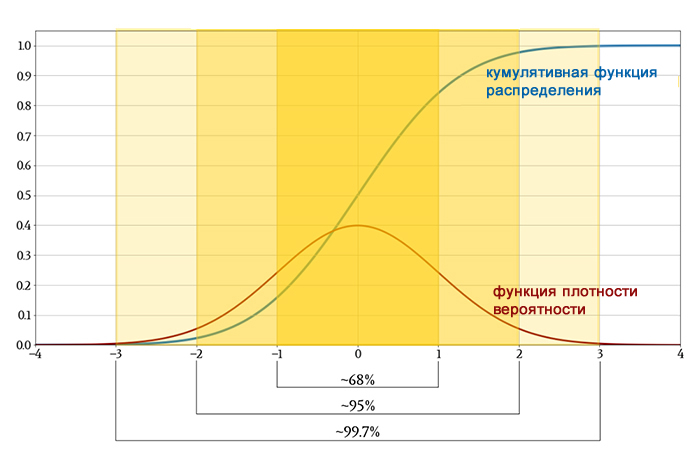
На следующем графике показаны как исходная гауссова функция плотности вероятности, так и ее функция распределения, чтобы вы могли увидеть, как интегрирование превращает одно в другое.

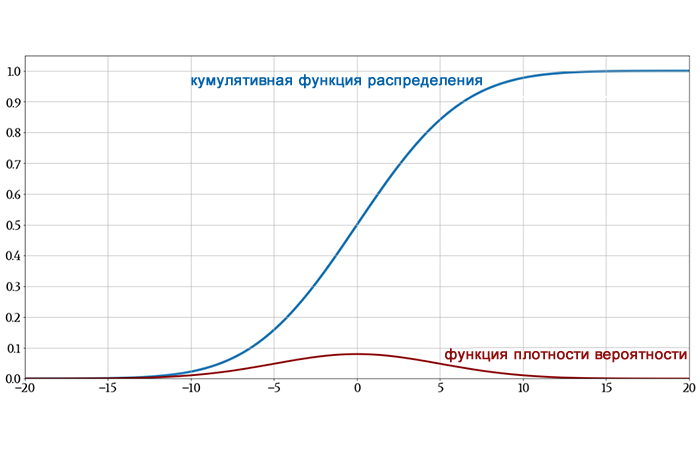
Одно небольшое замечание, прежде чем мы продолжим: в обсуждениях о статистике вы можете увидеть символ Φ (заглавная греческая буква фи). Когда нормальное распределение имеет среднее значение 0 и стандартное отклонение 1, оно называется стандартным нормальным распределением. Кумулятивная функция стандартного нормального распределения обозначается Φ; таким образом,

\[\Phi(z)=\frac{1}{\sqrt{2 \pi}}\int_{-\infty}^{z}e^{-\frac{x^2}{2}}dx\]

Пример кумулятивной функции распределения

Когда мы интегрируем функцию плотности вероятности от отрицательной бесконечности до некоторого значения, обозначенного z, мы вычисляем вероятность того, что результат случайно выбранного измерения или нового измерения попадет в числовой интервал, который простирается от отрицательной бесконечности до z. Другими словами, мы вычисляем вероятность того, что измеренное значение будет меньше z.

Это именно та информация, которую мы получаем из кумулятивной функции распределения и без необходимости интегрирования. Если мы посмотрим на график кумулятивной функции распределения и найдем вертикальное значение, соответствующее некоторому числу z на горизонтальной оси, мы узнаем вероятность того, что измеренное значение будет меньше z.

Например:

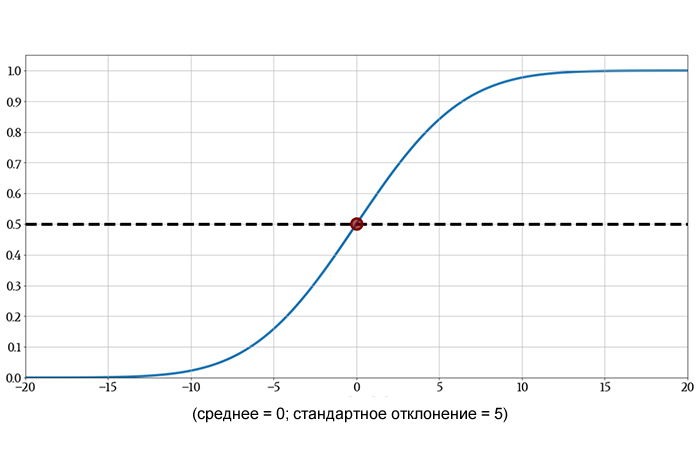
Кумулятивная функция распределения при z = 0 равна 0,5. Это говорит нам о том, что результат выбранного случайным образом измерения имеет 50% вероятность быть меньше нуля. Это интуитивно понятно: нормальное распределение симметрично относительно среднего, и поскольку среднее значение в этом случае равно нулю, любое отдельное измерение имеет равные шансы быть меньше или больше нуля.

Кумулятивная функция распределения (CDF) также обеспечивает простой способ определения вероятности того, что результат измерения попадет в определенный диапазон. Если диапазон определяется двумя значениями z₁ и z₂, всё, что нам нужно сделать, это вычесть значение функции распределения в z₂ из значения функции распределения в z₁ (а затем при необходимости взять модуль полученного значения).

Вот еще один пример:

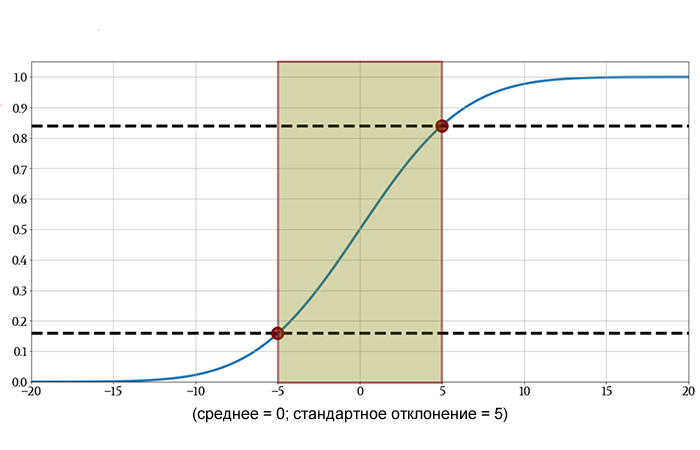
Вероятность того, что результат случайно выбранного измерения будет между –5 и +5, составляет приблизительно (0,84 – 0,16) = 0,68 (или 68%). Более точное значение – 68,27%.

Вероятность и стандартное отклонение

Вы могли заметить, что интервал, выбранный в предыдущем примере, был равен одному стандартному отклонению выше и ниже среднего. Когда мы обсуждаем вероятности со ссылкой на интервалы, представленные в единицах стандартного отклонения, эта информация применяется ко всем наборам данных, которые следуют нормальному распределению. Таким образом, мы можем определить вероятностные характеристики, используя кумулятивную функцию стандартного нормального распределения, а затем распространить эти тенденции на другие наборы данных, просто изменив стандартное отклонение (или размышляя относительно стандартных отклонений).

Выше мы видели, что в нормально распределенных данных измеренное значение имеет шанс 68,27% попасть в диапазон в пределах одного стандартного отклонения от среднего. Мы можем продолжить обобщение нормально распределенных данных следующим образом:

• вероятность того, что измеренное значение будет в пределах двух стандартных отклонений от среднего, составляет 95,45%;
• вероятность того, что измеренное значение будет в пределах трех стандартных отклонений от среднего, составляет 99,73%.

Эти три вероятности дают простое представление того, как будут вести себя нормально распределенные измерения.

Более приблизительная версия этого обобщения известна как правило 68-95-99,7: если набор данных демонстрирует нормальное распределение, около 68% значений будут в пределах одного стандартного отклонения от среднего, около 95% будут в пределах двух стандартных отклонений, и около 99,7% будут в пределах трех стандартных отклонений.

Заключение

Мы рассмотрели важный материал, и я надеюсь, что вам понравилось наше исследование нормального распределения и связанных с ним тем статистики. В следующей статье мы рассмотрим два малоизвестных описательных статистических показателя: асимметрию и эксцесс.

Теги