Понятие параметрических тестов, ассиметрии и эксцесса
В данной статье представлены важные категории логически выводимых статистических тестов и обсуждаются параметры описательной статистики, относящиеся к нормальному распределению.
Добро пожаловать в нашу серию статей о статистике в электротехнике. Ранее мы рассмотрели статистический анализ и описательный анализ в электротехнике, а затем обсудили среднее отклонение, стандартное отклонение и дисперсию в обработке сигналов.
Затем мы рассмотрели компенсацию размера выборки при расчетах стандартного отклонения и то, как стандартное отклонение связано со среднеквадратичными значениями.
Теперь мы перешли к исследованию нормального распределения в электротехнике, в частности, как понимать гистограммы, вероятность и кумулятивную функцию распределения нормально распределенных данных. Данная статья расширяет это обсуждение, касаясь параметрических тестов, асимметрии и эксцесса.
Когда нормальное распределение не выглядит нормальным
В предыдущих статьях мы рассмотрели нормальное распределение (также известное как распределение Гаусса) как идеализированное математическое распределение и как гистограмму, полученную из эмпирических данных. Если измеряемое явление характеризуется нормальным распределением значений, форма гистограммы по мере увеличения размера выборки будет всё больше похожа на колоколообразную (гауссову) кривую.
Однако это приводит нас к интересному вопросу: как мы узнаем, что явление характеризуется нормальным распределением значений?
Если у нас есть большой объем данных, мы можем просто посмотреть на гистограмму и сравнить ее с гауссовой кривой. Однако с меньшими наборами данных ситуация будет сложнее. Даже если мы анализируем базовый процесс, который действительно создает нормально распределенные данные, гистограммы, созданные из небольших наборов данных, могут оставлять место для сомнений.
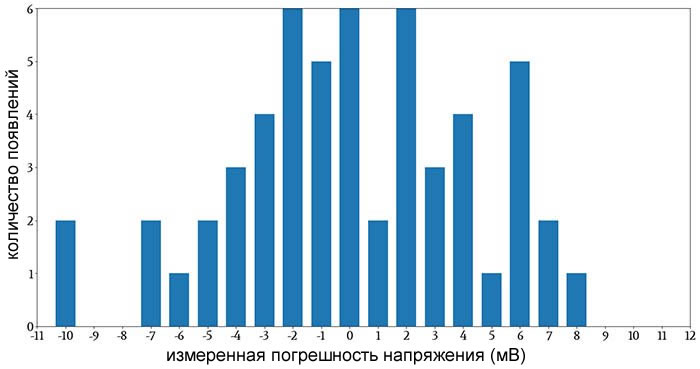
В данной статье мы обсудим два описательных статистических показателя (асимметрию и эксцесс), которые помогут нам определить, соответствуют ли наши данные нормальному распределению.
Однако сначала я хочу изучить связанный с этим вопрос: почему нас волнует, соответствует ли набор данных нормальному распределению?
Параметрические и непараметрические тесты
Существуют различные статистические методы, помогающие нам анализировать и интерпретировать данные, и некоторые из этих методов относятся к категории статистических выводов. Мы часто используем слово «тест», когда говорим о статистической процедуре вывода, и эти тесты могут быть параметрическими или непараметрическими.
Различие между параметрическими и непараметрическими тестами заключается в характере данных, к которым применяется тест. Когда набор данных демонстрирует распределение, которое в достаточной степени согласуется с нормальным распределением, можно использовать параметрические тесты. Когда данные не распределены нормально, мы переходим к непараметрическим тестам.
Примерами параметрических тестов являются парный t-критерий, односторонний дисперсионный анализ (ANOVA) и коэффициент корреляции Пирсона. Непараметрическими альтернативами этим критериям являются, соответственно, критерий знаковых рангов Уилкоксона, критерий Краскела–Уоллиса и ранговая корреляция Спирмена.
Почему «параметрический» и «непараметрический»?
Если вас смущает эта терминология параметрический/непараметрический, вот объяснение: параметр – это характеристика всей генеральной совокупности (совокупности значений), например, средний рост всех канадцев или стандартное отклонение выходных напряжений, генерируемых всеми микросхемами эталонного напряжения REF100 (я придумал эту модель микросхемы).
Обычно мы не можем знать параметр с уверенностью потому, что наши данные представляют собой только выборку из генеральной совокупности. Однако мы можем произвести оценку параметра, вычислив соответствующее статистическое значение на основе выборки.
Параметрические тесты основываются на предположениях, связанных с нормальностью распределения генеральной совокупности, и параметрами, которые характеризуют это распределение. Когда данные не распределены нормально, мы не можем делать такие предположения, и, следовательно, мы должны использовать непараметрические тесты.
Зачем заморачиваться с параметрическими тестами?
Если существуют непараметрические тесты и их можно применять независимо от нормальности распределения, зачем утруждать себя определением, является ли распределение нормальным? Давайте, просто применим непараметрический тест и покончим с этим!
Есть простая причина, по которой мы избегаем непараметрических тестов, когда данные достаточно нормальны: параметрические тесты, как правило, более эффективны. «Эффективность» в статистическом смысле означает, насколько эффективно тест обнаружит взаимосвязь между переменными (если эта взаимосвязь существует). Мы можем сделать любой тип тестов более эффективным, увеличив размер выборки, но для того, чтобы получить наилучшую информацию из имеющихся данных, мы по возможности используем параметрические тесты.
Оценка нормальности: асимметрия и эксцесс
Мы можем попытаться определить, демонстрируют ли эмпирические данные неопределенно нормальное распределение, просто взглянув на гистограмму. Однако, чтобы решить, является ли распределение достаточно нормальным, чтобы оправдать использование параметрических тестов, нам могут потребоваться дополнительные аналитические методы.
Асимметрия
Один из этих методов – вычислить асимметрию набора данных. Нормальное распределение идеально симметрично относительно среднего, и, таким образом, любое отклонение от идеальной симметрии указывает на некоторую степень ненормальности измеренного распределения.
На следующем рисунке представлены примеры асимметричных форм распределения.
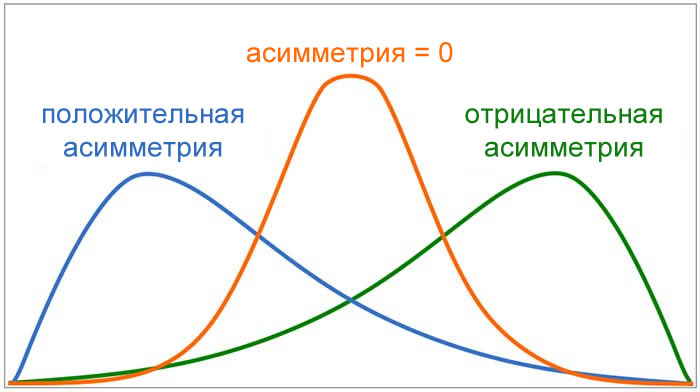
Асимметрия может представляться положительным или отрицательным числом (или нулем). Распределения, симметричные относительно среднего значения, такие как нормальное распределение, имеют нулевую асимметрию. Распределение, которое «наклоняется» вправо, имеет отрицательную асимметрию, а распределение, которое «наклоняется» влево, имеет положительную асимметрию.
Как правило, значения асимметрии, которые находятся в пределах ±1 от асимметрии нормального распределения, указывают на достаточную нормальность для использования параметрических тестов.
Эксцесс
Мы используем эксцесс, чтобы количественно оценить тенденцию явления создавать значения, далекие от среднего. Существуют различные способы описания информации, которую эксцесс передает о наборе данных: «хвостатость» (обратите внимание, что значения, далекие от среднего, находятся в хвостах распределения), «величина хвоста» или «вес хвоста» и «островершинность» (последнее несколько проблематично, потому что эксцесс напрямую не измеряет остроту или гладкость).
Нормальное распределение имеет значение эксцесса 3. Следующая диаграмма дает общее представление о том, как эксцесс больше или меньше 3 соответствует формам ненормального распределения.
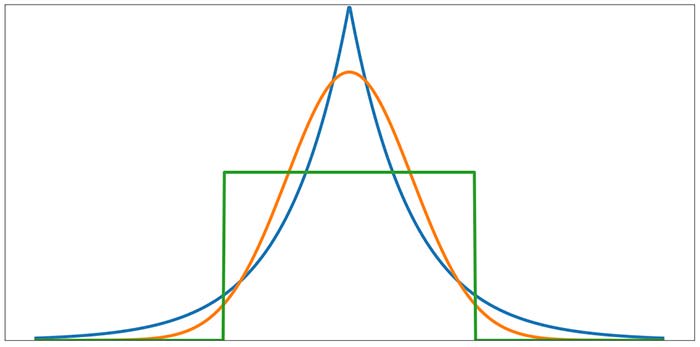
Оранжевая кривая – нормальное распределение. Обратите внимание, что синяя кривая по сравнению с оранжевой кривой имеет большую «величину хвоста», то есть большую массу вероятности в хвостах. Эксцесс синей кривой, которая называется распределением Лапласа, равен 6. Зеленая кривая называется равномерным распределением; вы можете видеть, что хвосты отсутствуют. Эксцесс равномерного распределения равен 1,8.
Как и в случае асимметрии, общее правило состоит в том, что эксцесс в пределах ±1 от эксцесса нормального распределения указывает на достаточную нормальность.
Заключение
Конечно, о параметрических тестах, асимметрии и эксцессе можно сказать гораздо больше, но я думаю, что мы рассмотрели достаточно материала для вводной статьи. Обобщим вышесказанное:
- когда результаты измерений показывают достаточно нормальное распределение, мы предпочитаем параметрические тесты;
- асимметрия количественно определяет отсутствие симметрии распределения относительно среднего значения;
- эксцесс количественно определяет «хвостатость» распределения и передает тенденцию явления к получению значений, далеких от среднего.
