Нахождение статистических связей с помощью коэффициентов корреляции
Коэффициенты корреляции Пирсона и Спирмена представляют собой стандартные методы для вывода о причинно-следственной связи путем вычисления силы линейной или монотонной связи между двумя переменными.
В этой серии статей исследуется, как инженеры-электронщики используют статистику. Если вы только присоединяетесь к обсуждению, то, возможно, захотите просмотреть предыдущие статьи этой серии. Полный список статей можно найти в меню с оглавлением над статьей.
Краткий обзор ковариации, корреляции и причинно-следственной связи
В предыдущей статье мы обсудили ковариацию, корреляцию и причинно-следственную связь.
- Дисперсия количественно определяет мощность случайных отклонений в наборе данных.
- Ковариация количественно определяет взаимосвязь между отклонениями в двух отдельных наборах данных. Более конкретно, она фиксирует склонность значений в двух наборах данных к изменению вместе (то есть к совместному изменению) линейным образом.
- Ковариация измеряет корреляцию двух переменных.
- Корреляция не доказывает причинно-следственную связь – если две переменные коррелированы, мы не можем автоматически сделать вывод, что изменения в одной переменной вызывают изменения в другой переменной. Тем не менее, если мы подозреваем наличие причинно-следственной связи и можем продемонстрировать корреляцию, у нас есть веские основания для дальнейшего изучения возможности причинной связи путем сбора дополнительных данных или проведения новых экспериментов.
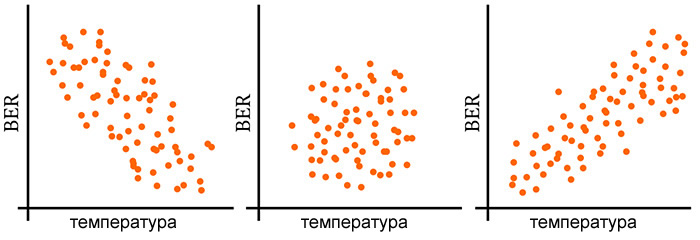
Интерпретация ковариации
Для двух наборов данных с размером выборки N мы вычисляем ковариацию следующим образом:
\(\operatorname {cov} (X,Y)=\frac{1}{N-1}\sum_{i=1}^{N}(X_i-\operatorname {E}[X])(Y_i-\operatorname {E}[Y])\)
(Если данная формула вас немного запутывает, то в предыдущей статье дается ее объяснение.) Давайте на мгновение задумаемся о том, что произошло бы, если бы мы вычислили ковариацию между набором данных и им самим:
\(\operatorname {cov} (X,X)=\frac{1}{N-1}\sum_{i=1}^{N}(X_i-\operatorname {E}[X])(E_i-\operatorname {E}[X])=\frac{1}{N-1}\sum_{i=1}^{N}(X_i-\operatorname {E}[X])^2\)
Формула ковариации стала формулой дисперсии. Поскольку набор данных идеально коррелирует сам с собой, мы видим, что существует связь между дисперсией и максимально возможным значением ковариации.
Эта связь распространяется на стандартное отклонение, потому что дисперсия равна квадрату стандартного отклонения. Таким образом, ковариация между набором данных и самим собой равна квадрату стандартного отклонения, то есть SD(X)SD(X).
Если мы расширим это на общий случай, в котором мы вычисляем ковариацию двух разных наборов данных, мы можем сказать, что идеальная линейная корреляция (и, следовательно, максимальная ковариация) соответствует значению ковариации, которое равно стандартному отклонению первого набора данных, умноженному на стандартное отклонение второго набора данных:
\(\operatorname {cov} (X,Y)_{MAX}=\operatorname {SD} (X)\operatorname {SD} (Y)\)
Та же логика применима к двум наборам данных, которые демонстрируют идеальную обратную корреляцию. Таким образом,
\(\operatorname {cov} (X,Y)_{MIN}=-\operatorname {SD} (X)\operatorname {SD} (Y)\)
Теперь у нас есть информация, необходимая для интерпретации значений ковариации. Диапазон ковариации простирается от –SD(X)SD(Y), что указывает на идеальную обратную линейную корреляцию, до +SD(X)SD(Y), что указывает на идеальную линейную корреляцию. В середине этого диапазона стоит ноль, что свидетельствует о полном отсутствии линейной корреляции.
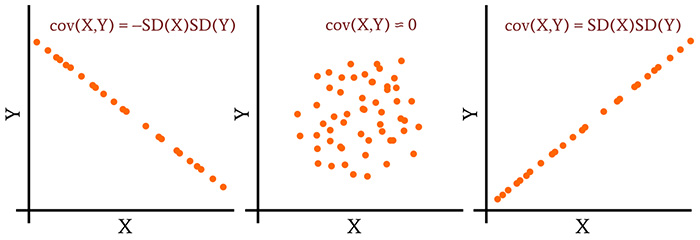
Коэффициент корреляции Пирсона
Теперь мы можем понять, почему ковариация с практической точки зрения очень неудобна. Заданная степень корреляции может соответствовать совершенно разным значениям ковариации, потому что диапазон ковариации определяется стандартными отклонениями двух наборов данных.
Таким образом, мы не можем просто сказать о ковариации и ожидать, что наши коллеги поймут важность нашего анализа. Мы должны сообщать о ковариации и стандартных отклонениях, а наиболее разумный способ сделать это – включить стандартные отклонения в корреляционный анализ. Это то, что мы называем коэффициентом корреляции Пирсона:
\(\rho_{X,Y}=\frac{\operatorname{cov}(X,Y)}{SD(X)SD(Y)}\)
где ρX,Y – коэффициент корреляции Пирсона для переменных X и Y (ρ – греческое ро в нижнем регистре). Как видите, мы просто применили проверенный временем метод нормализации.
Когда мы делим ковариацию на произведение двух стандартных отклонений, мы нормализуем ковариацию так, чтобы каждая пара наборов данных давала значение в диапазоне [–1, +1]. В результате получается легко интерпретируемая мера линейной корреляции, позволяющая проводить прямые сравнения.
Как это часто бывает в статистике, нам необходимо проводить различие между генеральной совокупностью (популяцией) и выборкой. Символ ρ обозначает коэффициент корреляции Пирсона для генеральной совокупности. Когда мы вычисляем корреляцию Пирсона для выборки, мы используем букву r:
\(r_{xy}={\frac {\sum _{i=1}^{N}(x_{i}-{\bar {x}})(y_{i}-{\bar {y}})}{{\sqrt {\sum _{i=1}^{N}(x_{i}-{\bar {x}})^{2}}}{\sqrt {\sum _{i=1}^{N}(y_{i}-{\bar {y}})^{2}}}}}\)
Обратите внимание, что члены 1/(N-1) сокращаются. Кроме того, вы, возможно, не знакомы с горизонтальной полосой над X и Y: это еще один метод обозначения среднего, он используется специально для среднего значения выборки, а не генеральной совокупности. Среднее значение для генеральной совокупности обозначается символом μ .
Коэффициент корреляции Спирмена
Как вы, возможно, читали в предыдущей статье, некоторые статистические тесты (называемые параметрическими тестами) могут применяться только к данным, которые демонстрируют достаточно нормальное распределение. Коэффициент корреляции Пирсона – это параметрический тест, и, следовательно, если ваши данные недостаточно нормальны, вам необходимо рассмотреть непараметрическую альтернативу.
Непараметрическая версия коэффициента корреляции Пирсона называется коэффициентом ранговой корреляции Спирмена. Формула та же самая, но применяется к ранговым переменным и количественно определяет монотонную корреляцию вместо линейной корреляции.
Заключение
Коэффициент корреляции Пирсона – ценный и широко используемый статистический показатель, который помогает выявить значимые и потенциально причинно-следственные связи между переменными. Это важно для эмпирических исследований, и когда-нибудь это может даже пригодиться при устранении неисправности в электронной системе.
