Статистическая значимость в экспериментах и анализе данных
Что именно имеют в виду ученые и исследователи, когда заявляют, что что-то является или не является статистически значимым? Как установить статистическую значимость и как ее интерпретировать?
Добро пожаловать в 11-ю часть серии статей о статистике в электротехнике. До сих пор мы рассматривали как высокоуровневые определения, так и конкретные примеры статистических концепций, полезных для инженера-практика. Чтобы узнать больше о том, что мы рассмотрели, ознакомьтесь со статьями, перечисленными в меню с оглавлением выше, над статьей.
Статистическая значимость: туманная концепция?
Любой, кто обычно читает исследовательские статьи, часто сталкивается со «статистической значимостью», часто сопровождаемой загадочной ссылкой на p<0,01 или p<0,05.
Статистическая значимость – это базовый инструмент, который помогает исследователям понять, что на самом деле показали их эксперименты и их данные, и помогает коллегам решить, заслуживают ли сообщенные результаты дальнейшего рассмотрения или исследования.
В то же время статистическая значимость – это несколько туманное понятие, которое легко неверно истолковать и которое вызвало немало споров в научном сообществе.
Фактически, не так давно три профессора опубликовали статью «комментарий» в журнале Nature, в которой рекомендовалось полностью отказаться от статистической значимости как основы для принятия или отклонения гипотезы – и им потребовалась всего одна неделя, чтобы найти 800 других ученых и исследователей, которые были готовы выразить формальное согласие с их позицией.
Что такое статистическая значимость?
Эксперимент начинается с нулевой гипотезы, которая утверждает, что нет никакой связи между двумя явлениями, для которых будут собираться данные. Если цель эксперимента состоит в том, чтобы найти или продемонстрировать какой-то тип взаимосвязи или влияние, нулевая гипотеза равносильна утверждению, что эксперимент «потерпел неудачу».
Статистическая значимость – это математический критерий, который мы можем использовать, чтобы решить, следует ли нам принять или отвергнуть нулевую гипотезу.
Статистически значимый результат на основе заранее определенного порога вероятности указывает на то, что мы должны отклонить нулевую гипотезу; другими словами, что-то действительно произошло (связь наблюдалась, было произведено влияние, связь существует), и поэтому эксперимент выявил что-то потенциально значимое или интересное.
Явления, управляемые случайными процессами, обычно приводят к нормальному распределению значений. Таким образом, общепринято представлять концептуальную нулевую гипотезу в виде гауссовой кривой, что означает, что это распределение наблюдений, которое мы ожидаем, когда одна экспериментальная переменная не зависит от другой экспериментальной переменной.
Порог вероятности
Статистическая значимость основана на вероятности получения результата при предположении, что нулевая гипотеза верна. Предположим, что в ходе нашего эксперимента мы получили число x (это может быть что угодно: артериальное давление, доход от продаж, средний балл теста).
Обращаясь к функции плотности вероятности, связанной с нулевой гипотезой, мы можем определить, будет ли вероятность получения x или какого-либо другого числа, которое более маловероятно, чем x, менее 5% (p <0,05) или 1% ( p <0,01) или какой-либо другого порога (p <⍺, где ⍺ обозначает требуемый уровень значимости).
Таким образом, p-значение (p-value, p-уровень значимости, p-критерий) передает вероятность получения результата, равного или более экстремального, чем наблюдаемый результат, когда нет взаимосвязи между интересующими переменными.
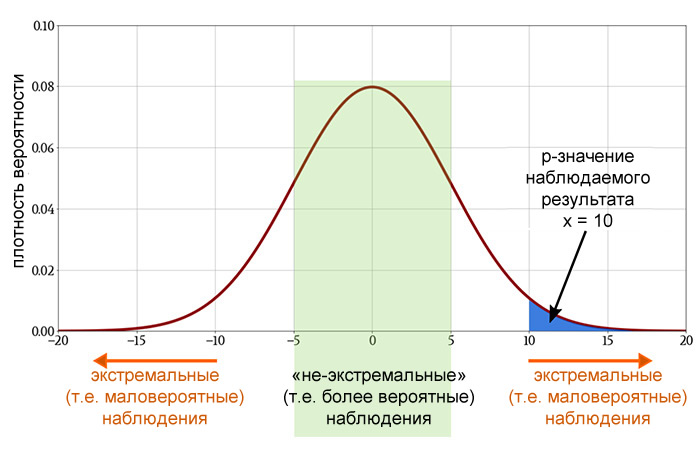
Если p-значение достаточно низкое, нет смысла продолжать предполагать, что между двумя переменными нет никакой связи. Таким образом, мы отвергаем нулевую гипотезу и утверждаем, что связь существует.
Интерпретация статистической значимости
Предыдущее объяснение описывает статистическую значимость способом, который я считаю наиболее простым и математически последовательным: если p-значение наблюдаемого результата меньше заранее определенного порога, который мы называем уровнем значимости, наблюдаемый результат очень маловероятен, если нулевая гипотеза верна. Поэтому, когда мы отвергаем нулевую гипотезу, это равносильно подтверждению того, что эксперимент обнаружил связь между интересующими переменными.
Это же общее сообщение можно передать другими способами, которые могут оказаться полезными:
- p-значение – это вероятность того, что наши наблюдения являются чистой случайностью. Таким образом, если p = 0,05, существует 5%-ная вероятность того, что результат является случайным, и 95%-ная вероятность того, что это связано с условиями, которые мы создали в нашем эксперименте.
- p-значение – это вероятность того, что мы неправильно сделаем вывод о взаимосвязи между интересующими нас переменными. Таким образом, значение p, равное 0,05, означает, что на каждые 100 экспериментов, в которых мы вывели взаимосвязь, 95 из этих взаимосвязей действительно существовали, а 5 не существовали.
Толкование слова «значимость»
Большая путаница в отношении статистической значимости возникает из-за использования слова «значимость», которое в данном контексте ограничивается конкретным статистическим использованием и не совпадает со словом «значимость» в обычном языке.
Статистически значимые результаты не обязательно являются важными или значимыми результатами. Статистическая значимость не означает практической значимости, а также отсутствие статистической значимости не означает, что экспериментальные результаты не имеют практической ценности.
Уровень значимости
Чтобы установить статистическую значимость, мы должны сравнить p-значение с уровнем значимости, обозначенным как ⍺. Уровни значимости в некоторой степени произвольны и выбираются в соответствии с условиями заданной области. Как было указано выше, часто используются ⍺ = 0,05 и ⍺ = 0,01, хотя в некоторых случаях выбирается более высокое или гораздо более низкое значение.
Заключение
Несмотря на возможное неправильное использование статистической значимости и доказательства широко распространенной неверной интерпретации, она остается важным методом в исследованиях и экспериментах. Мы продолжим изучение этой темы в следующей статье.
