Согласование импедансов и диаграмма Смита
Аннотация: Руководство по согласованию РЧ импедансов с использованием диаграммы Смита. На примерах показано, как отмечать на диаграмме коэффициенты отражения, импедансы и проводимости. В примерах с использованием графических методов разработаны две схемы согласования импедансов на частотах 60 МГц и 900 МГц.
Проверенная временем диаграмма Смита по-прежнему остается основным инструментом для определения полного сопротивления линии передачи.
При практической реализации высокочастотных приложений всегда возникают кошмарные задачи. Во-первых, необходимо согласовать разные импедансы соединенных между собой блоков. Обычно это подключение антенны к малошумящему усилителю (LNA), выхода усилителя мощности (RFOUT) к антенне и выходов LNA/VCO к входам смесителя. Задача согласования требуется для правильной передачи сигнала и мощности от «источника» к «нагрузке».
На высоких радиочастотах паразитные элементы (такие как индуктивность проводов, межслойные емкости и сопротивление проводов) оказывают значительное, но непредсказуемое влияние на согласующую цепь. Выше нескольких десятков мегагерц теоретических расчетов и моделирования часто бывает недостаточно. Для определения правильных окончательных значений необходимо учитывать лабораторные измерения ВЧ сигнала на месте, а также работу по настройке. Вычисленные значения требуются для выбора типа структуры и целевых значений компонентов.
Существует множество способов согласования импедансов, в том числе:
- компьютерное моделирование: сложное, но простое в использовании, поскольку такие симуляторы предназначены для различных функций разработки, а не только для согласования импедансов. Разработчики должны знать множество входных данных, которые необходимо ввести, и правильные форматы. Им также необходим опыт, чтобы найти полезные данные среди множества получаемых результатов. Кроме того, программное обеспечение для моделирования схем не устанавливается на компьютеры заранее, если только они не предназначены для такого применения;
- вычисления вручную: утомительно из-за («километровой») длины уравнений и комплексной природы чисел, которыми нужно манипулировать;
- интуиция: ее можно приобрести только после того, как человек много лет посвятил индустрии радиочастотной техники. Короче, это для суперспециалиста;
- диаграмма Смита: на которой сконцентрировано внимание в данной статье.
Основная цель этой статьи – рассмотреть конструкцию и предысторию диаграммы Смита, а также обобщить практические способы ее использования. Рассматриваемые темы включают в себя практические примеры, такие как поиск значений компонентов согласующей цепи. Конечно согласование для передачи максимальной мощности – не единственное, что мы можем сделать с помощью диаграмм Смита. Они также могут помочь проектировщику с такими задачами, как оптимизация для достижения наилучших показателей шума, обеспечение влияния добротности и оценка анализа устойчивости.
Краткое введение
Перед тем, как представить использование диаграммы Смита, было бы неплохо представить краткий обзор явления распространения волн для разводки микросхем в условиях РЧ сигналов (выше 100 МГц). Это может быть справедливо и для непредвиденных обстоятельств, таких как линии RS-485, и для предвиденных: между усилителем мощности и антенной, между LNA и понижающим преобразователем/смесителем и т.д.
Хорошо известно, что для достижения передачи максимальной мощности от источника к нагрузке полное сопротивление источника должно равняться комплексно-сопряженной величине полного сопротивления нагрузки, или:
\[R_и +jX_и = R_н - jX_н\]
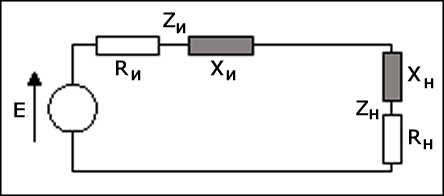
Для этого условия мощность, передаваемая от источника к нагрузке, максимальна. Кроме эффективной передачи мощности, это условие необходимо, чтобы избежать отражения мощности от нагрузки обратно к источнику. Это особенно верно для высокочастотных приложений, таких как радиочастотные и СВЧ цепи.
Что такое диаграмма Смита
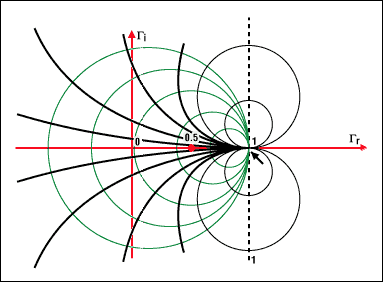
Диаграмма Смита представляет собой круговой график с множеством переплетенных окружностей. При правильном использовании согласование импедансов (с очевидно сложной структурой) может быть выполнено без каких-либо вычислений. Единственное, что требуется, – это считывать значения и следовать им по окружностям.
Диаграмма Смита представляет собой полярный график комплексного коэффициента отражения (обозначаемый символом Γ (гамма)). Математически он определяется как параметр рассеяния от порта 1, или s11.
Диаграмма Смита разрабатывается путем исследования нагрузки, импеданс которой должен быть согласован. Вместо того, чтобы напрямую рассматривать ее импеданс, вы выражаете ее коэффициент отражения Γн, который используется, чтобы охарактеризовать нагрузку. Γн более полезен при работе с радиочастотами.
Мы знаем, что коэффициент отражения определяется как отношение между отраженной волной напряжения и падающей волной напряжения:
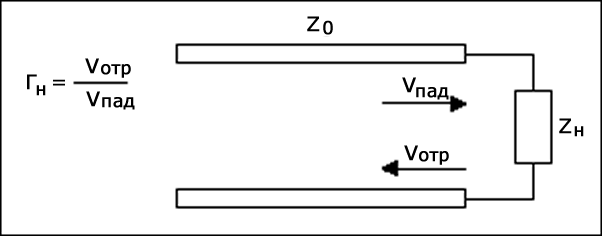
Количество отраженного сигнала от нагрузки зависит от степени рассогласования между импедансом источника и импедансом нагрузки. Его выражение было определено следующим образом:
\[\Gamma_н = \frac{Z_н}{Z_0} = \frac{Z_н - Z_0}{Z_н + Z_0} = \Gamma_r + j\Gamma_i \qquad (2.1)\]
Поскольку импедансы являются комплексными числами, коэффициент отражения также будет комплексным числом.
Чтобы уменьшить количество неизвестных параметров, полезно заморозить те, которые часто появляются и являются общими в приложении. Здесь Z0 (характеристическое сопротивление) часто является постоянным и действительным нормированным значением, например, 50 Ом, 75 Ом, 100 Ом и 600 Ом. Затем мы можем определить нормализованное сопротивление нагрузки следующим образом:
\[z = \frac{Z_н}{Z_0} = \frac{R + jX}{Z_0} = r + jx \qquad (2.2)\]
С таким упрощением мы можем переписать формулу коэффициента отражения как:
\[\Gamma_н =\Gamma_r + j\Gamma_i = \frac{Z_н - Z_0}{Z_н + Z_0} = \frac{(Z_н - Z_0)/Z_0}{(Z_н + Z_0)/Z_0} = \frac{z-1}{z+1} = \frac{r+jx-1}{r+jx+1} \qquad (2.3)\]
Здесь мы видим прямую зависимость между импедансом нагрузки и ее коэффициентом отражения. К сожалению, сложный характер этой зависимости практически бесполезен, поэтому мы можем использовать диаграмму Смита как тип графического представления показанного выше уравнения.
Чтобы построить диаграмму, это уравнение необходимо переписать, чтобы извлечь стандартные геометрические фигуры (например, окружности или случайные линии).
Во-первых, уравнение 2.3 переворачивается и дает:
\[z = r+jx = \frac{1+\Gamma_н}{1-\Gamma_н}= \frac{1+\Gamma_r+j\Gamma_i}{1-\Gamma_r-j\Gamma_i} \qquad (2.4)\]
а также
\[r = \frac{1-\Gamma^2_r-\Gamma^2_i} {1+\Gamma^2_r-2\Gamma_r+\Gamma^2_i} \qquad (2.5)\]
Уравнивая действительные и мнимые части уравнения 2.5, мы получаем два независимых новых соотношения:
\[r = \frac{1-\Gamma^2_r-\Gamma^2_i} {1+\Gamma^2_r-2\Gamma_r+\Gamma^2_i} \qquad (2.6)\]
\[x = \frac{2\Gamma^2_i} {1+\Gamma^2_r-2\Gamma_r+\Gamma^2_i} \qquad (2.7)\]
Уравнение 2.6 затем обрабатывается путем преобразования уравнений с 2.8 по 2.13 в окончательное уравнение 2.14. Это уравнение представляет собой соотношение в форме параметрического уравнения (x - a)² + (y - b)² = R² в комплексной плоскости (Γr, Γi) для окружности с центром в координатах [r/(r+1),0] и радиусом 1/(1+r).
\[r + r\Gamma^2_r - 2r\Gamma_r + r\Gamma^2_i = 1 - \Gamma^2_r - \Gamma^2_i \qquad (2.8)\]
\[\Gamma^2_r + r\Gamma^2_r - 2r\Gamma_r + r\Gamma^2_i + \Gamma^2_i = 1 -r \qquad (2.9)\]
\[(1+r)\Gamma^2_r - 2r\Gamma_r + (r + 1)\Gamma^2_i = 1 -r \qquad (2.10)\]
\[\Gamma^2_r - \frac{2r}{r+1}\Gamma_r + \Gamma^2_i = \frac{1 -r}{1+r} \qquad (2.11)\]
\[\Gamma^2_r - \frac{2r}{r+1}\Gamma_r + \frac{r^2}{(r+1)^2} + \Gamma^2_i - \frac{r^2}{(r+1)^2} = \frac{1 -r}{1+r} \qquad (2.12)\]
\[\left(\Gamma_r - \frac{r}{r+1}\right)^2 + \Gamma^2_i = \frac{1 -r}{1+r} + \frac{r^2}{(1 +r)^2} = \frac{1}{(1+r)^2} \qquad (2.13)\]
\[\left(\Gamma_r - \frac{r}{r+1}\right)^2 + \Gamma^2_i = \left(\frac{1}{1+r}\right)^2 \qquad (2.14)\]
Для получения дополнительной информации посмотрите на рисунок 4a.
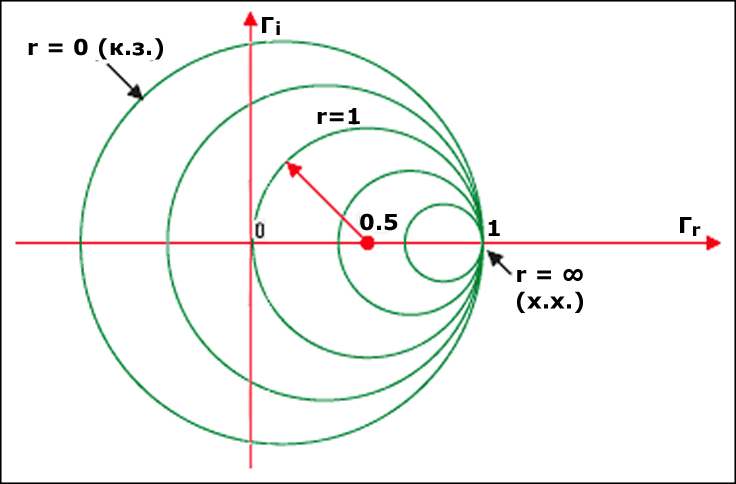
Точки, расположенные на окружности, представляют собой все импедансы, характеризующиеся одним и тем же значением действительной части импеданса. Например, окружность r = 1 имеет центр в координатах (0,5, 0) и радиус 0,5. Она включает в себя точку (0, 0), которая является нулевой точкой отражения (нагрузка согласована с характеристическим сопротивлением). Короткое замыкание в качестве нагрузки представляет собой круг с центром в координате (0, 0) и радиусом 1. Для разомкнутой цепи в качестве нагрузки окружность вырождается в одну точку (с центром в (1, 0) и радиусом 0). Это соответствует максимальному коэффициенту отражения, равному 1, при котором вся падающая волна отражается полностью.
При разработке диаграммы Смита следует соблюдать определенные меры предосторожности. Это одни из самых важных:
- все окружности имеют одну и ту же единственную точку пересечения в координате (1, 0);
- окружность с нулевым сопротивлением, на которой нет сопротивления (r = 0), является наибольшей;
- окружность бесконечного активного сопротивления сокращается до одной точки в точке (1, 0);
- не должно быть отрицательных активных сопротивлений. Если одно (или несколько) появится, мы столкнемся с возможностью возникновения колебаний;
- выбрать другое значение активного сопротивления можно, просто выбрав другую окружность, соответствующую новому значению.
Возвращаемся к рисованию
Двигаясь дальше, мы используем уравнения с 2.15 по 2.18 для дальнейшего преобразования уравнения 2.7 в другое параметрическое уравнение. Это преобразование приводит к уравнению 2.19.
\[x+x\Gamma^2_r-2x\Gamma_r+x\Gamma^2_i = 2\Gamma^2_i \qquad (2.15)\]
\[1+\Gamma^2_r-2\Gamma_r+\Gamma^2_i = \frac{ 2\Gamma^2_i }{x} \qquad (2.16)\]
\[\Gamma^2_r-2\Gamma_r+1+\Gamma^2_i -\frac{ 2 }{x}\Gamma^2_i = 0 \qquad (2.17)\]
\[\Gamma^2_r-2\Gamma_r+1+\Gamma^2_i -\frac{ 2 }{x}\Gamma^2_i +\frac{1}{x^2} - \frac{1}{x^2} = 0 \qquad (2.18)\]
\[(\Gamma_r -1)^2 + \left(\Gamma_i - \frac{1}{x}\right)^2 = \frac{1}{x^2} \qquad (2.19)\]
Опять же, 2.19 является параметрическим уравнением типа (x - a)² + (y - b)² = R² в комплексной плоскости (Γr, Γi) для окружности с центром в координатах (1, 1/x) и радиусом 1/x.
Для получения дополнительной информации посмотрите на рисунок 4b.
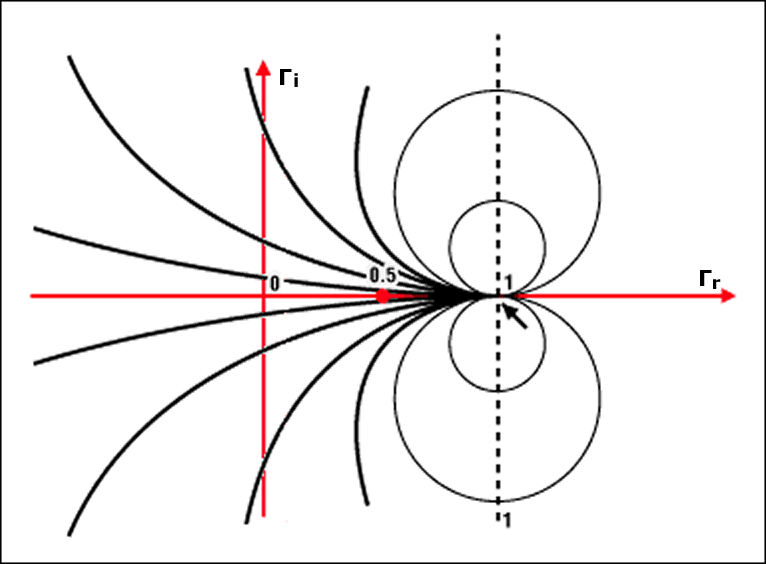
Точки, расположенные на окружности, представляют собой все импедансы, характеризующиеся одним и тем же значением мнимой части импеданса, x. Например, окружность x = 1 имеет центр в координате (1, 1) и радиус 1. Все окружности (с постоянным x) включают в себя точку (1, 0). В отличие от окружностей постоянной действительной части, x может быть положительным или отрицательным. Это объясняет повторяющиеся зеркальные окружности в нижней части комплексной плоскости. Центры всех окружностей расположены на вертикальной оси, пересекающей точку 1.
Получим полное изображение?
Чтобы завершить нашу диаграмму Смита, мы наложим эти два семейства окружностей. Тогда можно увидеть, что все окружности одного семейства будут пересекать все окружности другого семейства. Зная импеданс в виде r + jx, можно определить соответствующий коэффициент отражения. Необходимо только найти точку пересечения двух окружностей, соответствующих значениям r и x.
Справедливо и обратное
Возможна и обратная операция. Зная коэффициент отражения, можно найти две окружности, пересекающиеся в этой точке, и определить соответствующие значения r и х на окружностях. Процедура для этого следующая:
- определяем импеданс как точку на диаграмме Смита;
- находим коэффициент отражения (Γ) для этого импеданса;
- имея характеристическое сопротивление и Γ, находим полное сопротивление;
- преобразуем импеданс в полную проводимость;
- находим эквивалентный импеданс;
- находим значения компонентов для искомого коэффициента отражения (в частности, элементы согласующей цепи, смотрите рисунок 7).
Экстраполирование
Поскольку метод расчета с диаграммой Смита в основном является графическим методом, точность решений напрямую зависит от определений графиков. Вот пример, который может быть представлен диаграммой Смита для радиочастотных приложений:
Пример: рассмотрим характеристическое сопротивление оконечной нагрузки 50 Ом и следующие сопротивления:
| Z1 = 100 + j50 Ом | Z5 = ∞ (обрыв цепи) |
| Z2 = 75 - j100 Ом | Z6 = 0 (короткое замыкание) |
| Z3 = j200 Ом | Z7 = 50 Ом |
| Z4 = 150 Ом | Z8 = 184 - j900 Ом |
Затем выполним нормализацию и отметим эти точки на диаграмме (рисунок 5).
| z1 = 2 + j | z5 = 8 |
| z2 = 1,5 - j2 | z6 = 0 |
| z3 = j4 | z7 = 1 |
| z4 = 3 | z8 = 3,68 - j18 |
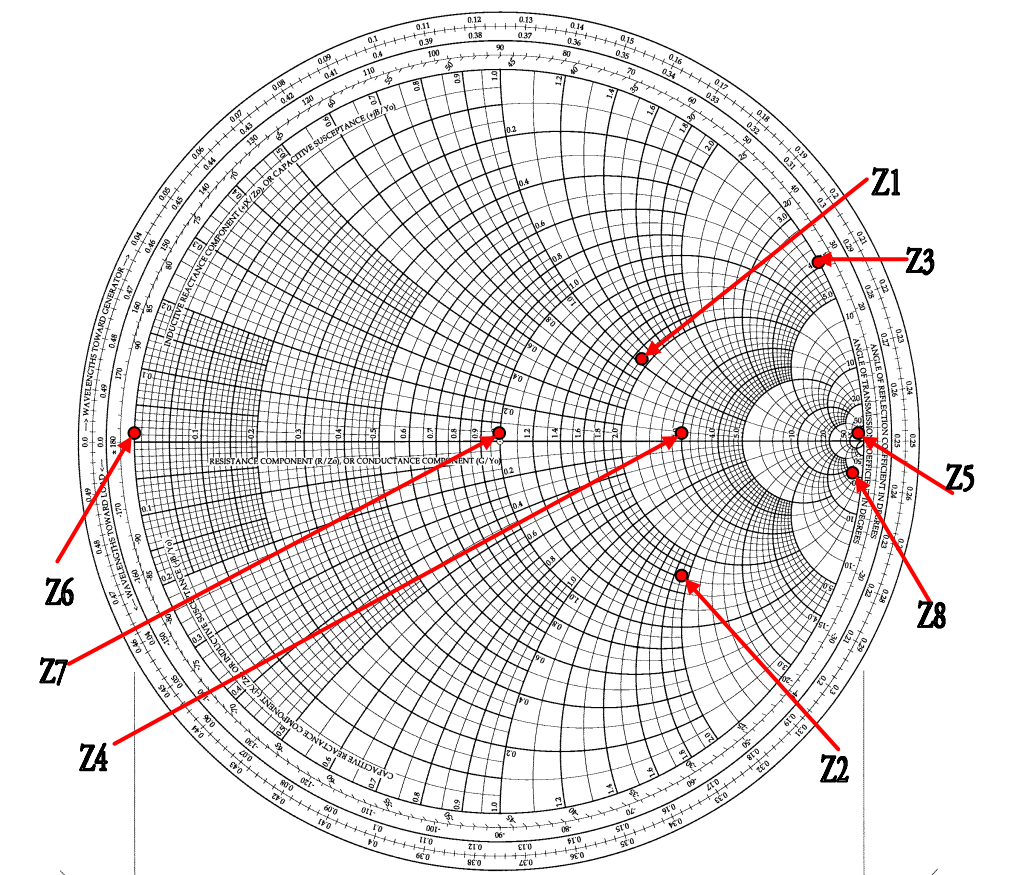
(больший масштаб – в файле PDF)
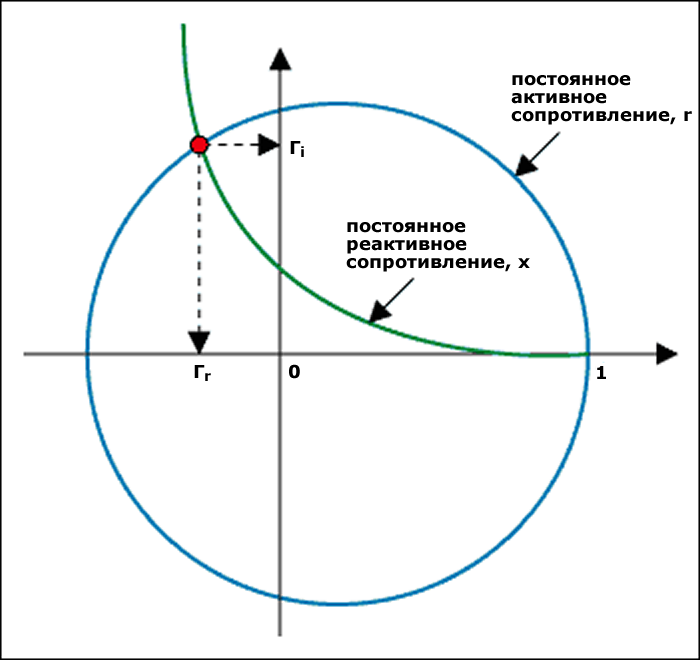
Теперь можно напрямую определить коэффициент отражения Γ по диаграмме Смита на рисунке 5. После того, как точка импеданса отложена (точка пересечения окружности постоянного сопротивления и дуги постоянного реактивного сопротивления), просто отложите прямоугольную проекцию координат на горизонтальную и вертикальную оси. Это даст Γr, действительную часть коэффициента отражения, и Γi, мнимую часть коэффициента отражения (рисунок 6).
Также можно взять восемь случаев, представленных в примере, и определить соответствующие им Γ непосредственно по диаграмме Смита, как показано на рисунке 6. Значения будут следующими:
| Γ1 = 0,4 + 0,2j | Γ5 = 1 |
| Γ2 = 0,51 - 0,4j | Γ6 = -1 |
| Γ3 = 0,875 + 0,48j | Γ7 = 0 |
| Γ4 = 0,5 | Γ8 = 0,96 - 0,1j |
Работа с полной проводимостью (адмиттансом)
Диаграмма Смита построена с учетом импеданса (активного и реактивного сопротивлений). После того, как диаграмма Смита построена, ее можно использовать для анализа параметров как в последовательном, так и в параллельном мире. Добавить элементы последовательно просто. Можно добавлять новые элементы и определять их влияние, просто перемещаясь по окружностям к их соответствующим значениям. Однако параллельное включение элементов – другое дело. Это требует учета дополнительных параметров. Часто с параллельными элементами проще работать в мире проводимостей.
Мы знаем, что по определению Y = 1/Z, а Z = 1/Y. Проводимость выражается сименсах, или См. И, поскольку Z является комплексным значением, Y также должна быть комплексным значением.
Следовательно,
\[Y = G + jB \qquad (2.20)\]
где
- Y – полная проводимость (адмиттанс, англ. «admitance»);
- G –действительная составляющая полной проводимости (англ. «conductance»);
- B – мнимая составляющая полной проводимости (англ. «susceptance»).
Здесь важно проявлять осторожность. Следуя логическому предположению, мы можем заключить, что G = 1/R, а B = 1/X. Однако это не так. Если использовать это предположение, результаты будут неверными.
При работе с полной проводимостью первое, что мы должны сделать, это нормализовать y = Y/Y0. Это приводит к y = g + jb. Итак, что происходит с коэффициентом отражения? Проработав следующее выражение:
\[\Gamma = \frac{Z_н - Z_0}{Z_н + Z_0} = \frac{1/Y_н - 1/Y_0}{1/Y_н + 1/Y_0} = \frac{Y_0 - Y_н}{Y_0 + Y_н} = \frac{1-y}{1+y} \qquad (2.21)\]
Оказывается, выражение для G противоположно по знаку выражению z, и Γ(y) = -Γ(z).
Если мы знаем z, мы можем поменять местами знаки Γ и найти точку, расположенную на том же расстоянии от (0, 0), но в противоположном направлении. Тот же результат может быть получен путем поворота на угол 180° вокруг центральной точки (рисунок 7).
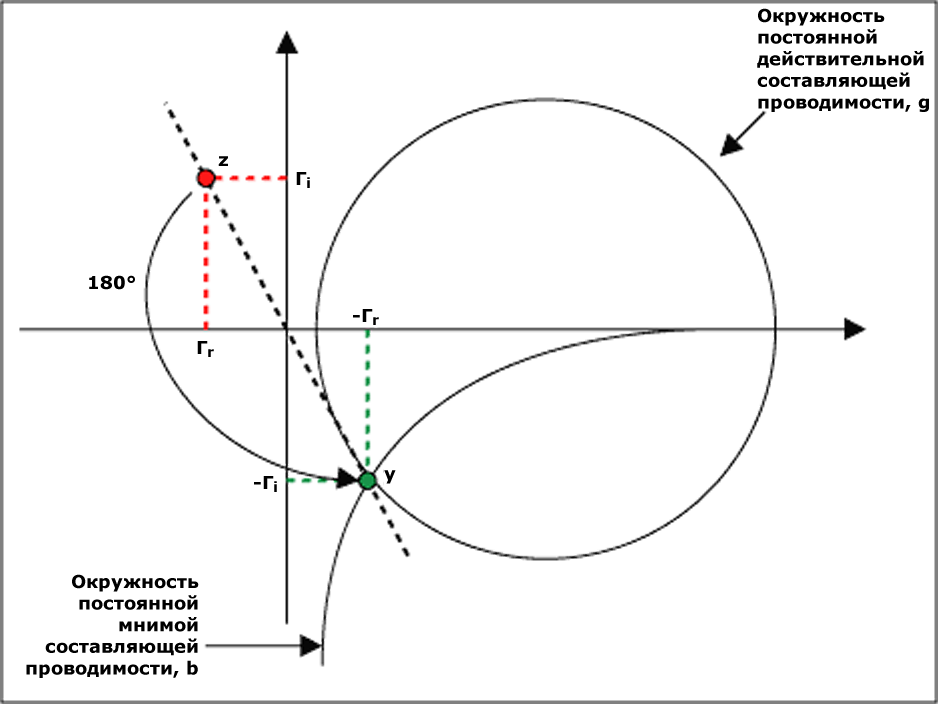
Конечно, хотя Z и 1/Y действительно представляют один и тот же компонент, новая точка отображается как другой импеданс (новое значение имеет другую точку на диаграмме Смита и другое значение коэффициента отражения и т.д.). Это происходит потому, что этот график представляет собой график импеданса. Но новая точка – это, по сути, адмиттанс (полная проводимость). Следовательно, значение, указанное на диаграмме, следует читать в сименсах.
Хотя этого метода достаточно для преобразования, он не работает для вычисления схемы при с параллельно включенными элементами.
Диаграмма Смита для проводимостей
В предыдущем разделе мы видели, что каждую точку на диаграмме Смита импеданса можно преобразовать в ее аналог проводимости, повернув на 180° вокруг начала координат комплексной плоскости Γ. Таким образом, диаграмму Смита полной проводимости можно получить, повернув всю диаграмму Смита полного сопротивления на 180°. Это очень удобно, так как избавляет от необходимости строить еще одну диаграмму. Точка пересечения всех окружностей (окружностей для постоянной действительной части полной проводимости и окружностей для постоянной мнимой части полной проводимости) автоматически будет в точке (-1, 0). С этой диаграммой также становится проще добавлять элементы параллельно. Математически построение диаграммы Смита для полной проводимости создается с помощью следующих выражений:
\[\Gamma_н = \Gamma_r + j\Gamma_i = \frac{1-y}{1+y} = \frac{1-g-jb}{1+g+jb} \qquad (3.1)\]
затем, переворачиваем уравнение:
\[y = g +jb = \frac{1-\Gamma_н}{1+\Gamma_н} = \frac{1-\Gamma_r - j\Gamma_i}{1+\Gamma_r + j\Gamma_i} \qquad (3.2)\]
\[g +jb = \frac{(1-\Gamma_r - j\Gamma_i)(1+\Gamma_r - j\Gamma_i)} {(1+\Gamma_r + j\Gamma_i)(1+\Gamma_r - j\Gamma_i)} = \frac{1-\Gamma^2_r - \Gamma^2_i - j2\Gamma_i} {1+\Gamma^2_r + 2\Gamma^2_r + \Gamma^2_i} \qquad (3.3)\]
Затем, приравнивая действительную и мнимую части уравнения 3.3, мы получаем два новых независимых соотношения:
\[g = \frac{1 - \Gamma^2_r - \Gamma^2_i} {1+\Gamma^2_r+2\Gamma_r+\Gamma^2_i} \qquad (3.4)\]
\[b = \frac{ - 2\Gamma_i} {1+\Gamma^2_r+2\Gamma_r+\Gamma^2_i} \qquad (3.5)\]
Развивая уравнение 3.4, мы получаем следующее:
\[g + g\Gamma^2_r+2g\Gamma_r+g\Gamma^2_i = 1 - \Gamma^2_r - \Gamma^2_i \qquad (3.6)\]
\[\Gamma^2_r+g\Gamma^2_r + 2g\Gamma_r+g\Gamma^2_i + \Gamma^2_i = 1 - g \qquad (3.7)\]
\[(1+g)\Gamma^2_r+ 2g\Gamma_r+(g+1)\Gamma^2_i = 1 - g \qquad (3.8)\]
\[\Gamma^2_r+ \frac{2g}{g+1}\Gamma_r+\Gamma^2_i = \frac{1 - g}{1 +g} \qquad (3.9)\]
\[\Gamma^2_r+ \frac{2g}{g+1}\Gamma_r +\frac{g^2}{(g+1)^2}+\Gamma^2_i -\frac{g^2}{(g+1)^2} = \frac{1 - g}{1 +g} \qquad (3.10)\]
\[\left(\Gamma_r+\frac{g}{g+1} \right)^2 +\Gamma^2_i = \frac{1 - g}{1 +g} + \frac{g^2}{(1+g)^2} = \frac{1}{(1+g)^2} \qquad (3.11)\]
\[\left(\Gamma_r+\frac{g}{g+1} \right)^2 +\Gamma^2_i = \left(\frac{1}{1+g}\right)^2 \qquad (3.12)\]
которое снова является параметрическим уравнением типа (x - a)² + (y - b)² = R² (уравнение 3.12) в комплексной плоскости (Γr, Γi) для окружности с координатами центра в [-g/(g+1), 0] и радиусом 1/(1+g).
Аналогично, развивая уравнение 3.5, мы получаем:
\[b +b\Gamma^2_r+2b\Gamma_r+b\Gamma^2_i = - 2\Gamma_i \qquad (3.13)\]
\[1 +\Gamma^2_r+2\Gamma_r+\Gamma^2_i = -\frac{2}{b}\Gamma_i \qquad (3.14)\]
\[\Gamma^2_r+2\Gamma_r +1+\Gamma^2_i + \frac{2}{b}\Gamma_i =0 \qquad (3.15)\]
\[\Gamma^2_r+2\Gamma_r +1+\Gamma^2_i + \frac{2}{b}\Gamma_i + \frac{1}{b^2} - \frac{1}{b^2} =0 \qquad (3.16)\]
\[(\Gamma_r+1)^2+ \left(\Gamma_i + \frac{1}{b} \right)^2 = \frac{1}{b^2} \qquad (3.17)\]
которое снова является параметрическим уравнением типа (x - a)² + (y - b)² = R² (уравнение 3.17).
Вычисление эквивалентного импеданса
При решении задач, в которых элементы, соединенные последовательно и параллельно, смешиваются вместе, мы можем использовать одну и ту же диаграмму Смита и вращать ее вокруг любой точки, где существуют преобразования из z в y или из y в z.
Рассмотрим схему на рисунке 8 (элементы нормированы с Z0 = 50 Ом). Последовательное реактивное сопротивление (x) положительно для индуктивности и отрицательно для емкости. Мнимая часть полной проводимости (b) положительна для емкости и отрицательна для индуктивности.
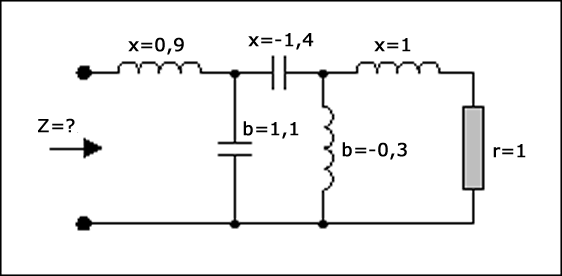
Эта схема требует упрощения (рисунок 9).
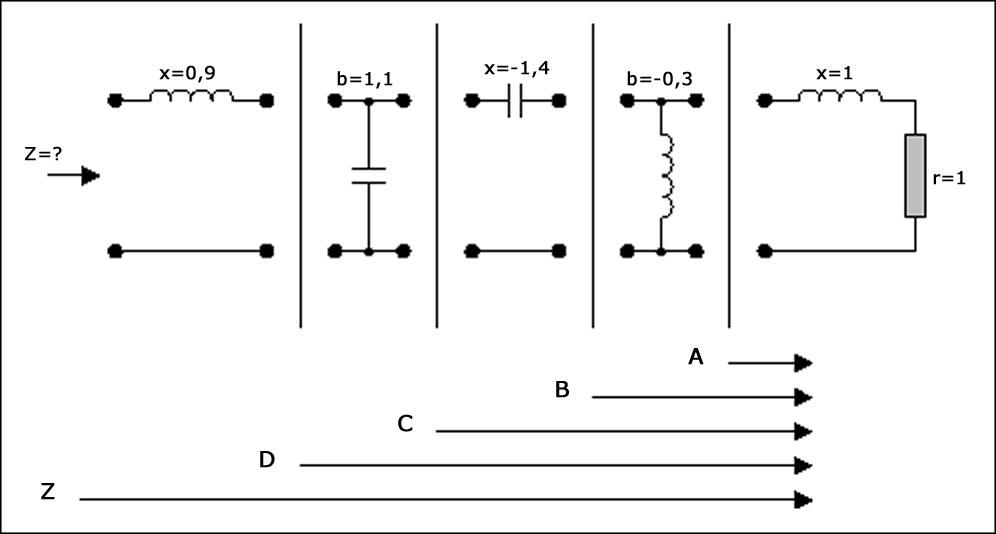
Начиная с правой стороны, где находятся резистор и катушка индуктивности со значением 1, мы строим последовательную точку, где пересекаются окружность r = 1 и окружность x = 1. Это становится точкой A. Поскольку следующим элементом является элемент в шунте (включен параллельно) переключаемся на диаграмму Смита для адмиттанса (вращая всю плоскость на 180°). Однако для этого нам нужно преобразовать предыдущую точку в адмиттанс. Она становится A'. Затем мы поворачиваем плоскость на 180°. Сейчас мы находимся в режиме адмиттанса. Шунтирующий элемент можно добавить, пройдя по окружности проводимости на расстояние, соответствующее 0,3. Это должно быть сделано против часовой стрелки (отрицательное значение) и дает точку B. Затем у нас идет еще один элемент, включенный последовательно. Мы снова переключаемся обратно на диаграмму Смита для импеданса.
Перед тем, как это сделать, необходимо снова преобразовать предыдущую точку в импеданс (это был адмиттанс). После преобразования мы можем определить B'. Используя ранее описанную процедуру, диаграмма снова поворачивается на 180°, чтобы вернуться в режим импеданса. Для добавления последовательного элемента необходимо пройти по окружности активного сопротивления на расстояние, соответствующее 1,4, и отметить точку C. Это нужно сделать против часовой стрелки (отрицательное значение). Для следующего элемента выполняется такая же операция (преобразование в адмиттанс и поворот плоскости). Затем перемещаемся на заданное расстояние (1,1) по часовой стрелке (поскольку значение положительное) вдоль окружности постоянной действительной составляющей проводимости. Мы отмечаем это как точку D. Наконец, мы возвращаемся обратно в режим импеданса и добавляем последний элемент (последовательную индуктивность). Затем определяем требуемое значение z, расположенное на пересечении окружности активного сопротивления 0,2 и окружности реактивного сопротивления 0,5. Таким образом, z определено равным 0,2 + j0,5. Если характеристическое сопротивление системы составляет 50 Ом, то Z = 10 + j25 Ом (рисунок 10).
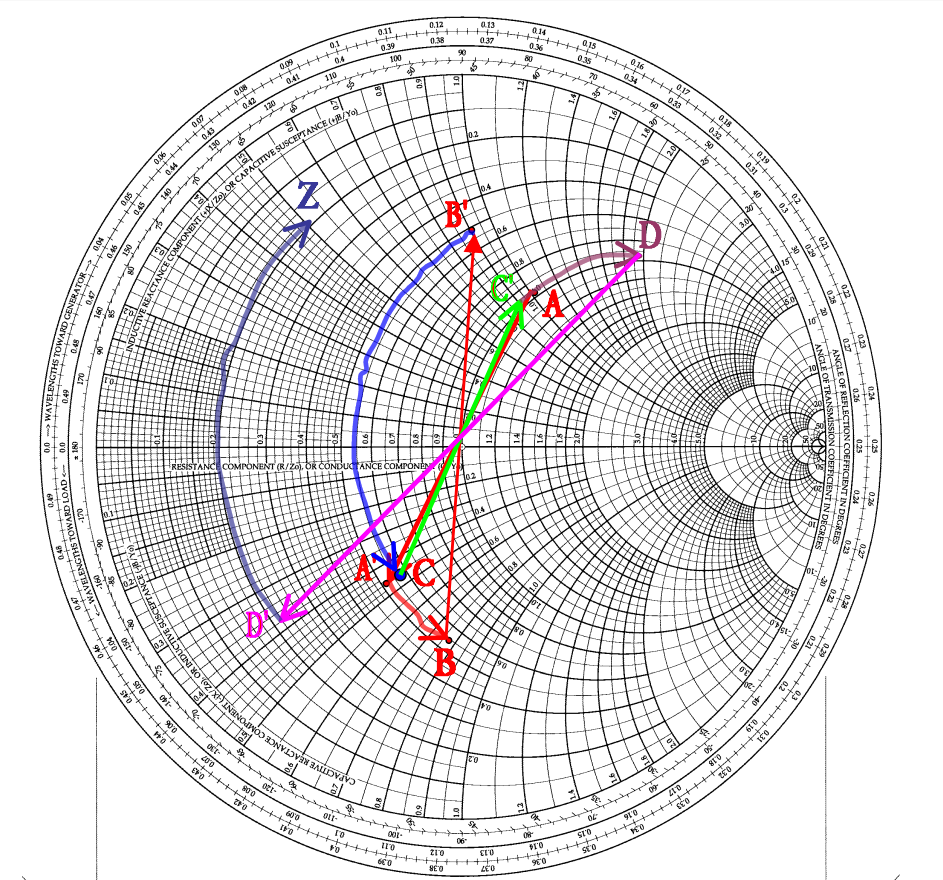
(больший масштаб – в файле PDF)
Пошаговое согласование импедансов
Другой функцией диаграммы Смита является возможность определения схемы согласования импедансов. Это операция, обратная нахождению эквивалентного импеданса заданной цепи. Здесь импедансы на двух концах зафиксированы (часто источник и нагрузка), как показано на рисунке 11. Задача состоит в том, чтобы спроектировать цепь, которая будет вставлена между ними, чтобы обеспечить надлежащее согласование импедансов.
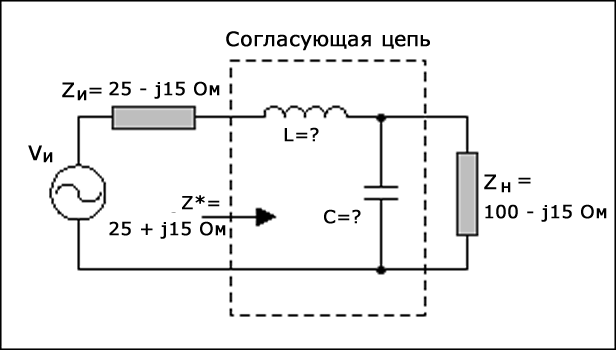
На первый взгляд, кажется, что это не сложнее, чем найти эквивалентное сопротивление. Но проблема в том, что может существовать бесконечное количество подходящих комбинаций компонентов цепи, которые дают аналогичные результаты. Также, возможно, должны быть рассмотрены и другие исходные данные (например, структура типа фильтра, добротность и ограниченный выбор компонентов).
Данный подход требует добавления последовательных и параллельных элементов на диаграмму Смита до тех пор, пока не будет достигнут необходимый импеданс. Графически это выглядит, как способ связать точки на диаграмме Смита. Опять же, лучший способ проиллюстрировать подход – рассмотреть на примере.
Задача состоит в том, чтобы согласовать полное сопротивление источника (Zи) с нагрузкой (Zн) на рабочей частоте 60 МГц (рисунок 11). Структура цепи была зафиксирована как фильтр нижних частот L-типа (альтернативный подход состоит в том, чтобы рассмотреть задачу, как заставить нагрузку проявляться как импеданс со значением, комплексно сопряженным с Zи). Вот как находится решение.
Первое, что нужно сделать, это нормализовать различные значения импеданса. Если нормализующее значение не указано, то выберите значение, которое находится в том же диапазоне, что и значения нагрузки/источника. Предположим, что Z0 равно 50 Ом. Таким образом,
\[z_и = 0,5 - j0,3 \\ z^*_и = 0,5 + j0,3 \\ z_н = 2 - j0,5\]
Затем отметьте две точки на графике. Отметьте A для zн и D для z*и (на рисунке 12 обозначена как Zs*).
Затем определите первый элемент, подключенный к нагрузке (конденсатор, включенный параллельно), и преобразуйте его в полную проводимость. Это дает нам точку А'.
Определите участок дуги, на котором появится следующая точка после подключения конденсатора C. Поскольку мы не знаем значение C, мы не знаем, где остановиться. Однако мы знаем направление. Параллельный C означает движение по часовой стрелке на диаграмме Смита, пока не будет найдено значение. Это будет точка B (адмиттанс). Поскольку следующий элемент включен последовательно, точка B должна быть преобразована в плоскость импеданса. Тогда можно предоставить точку B'. Точка B' должна быть расположена на той же окружности активного сопротивления, что и D. Графически существует только одно решение от A' до D, и промежуточную точку B (и, следовательно, B') необходимо найти методом проб.
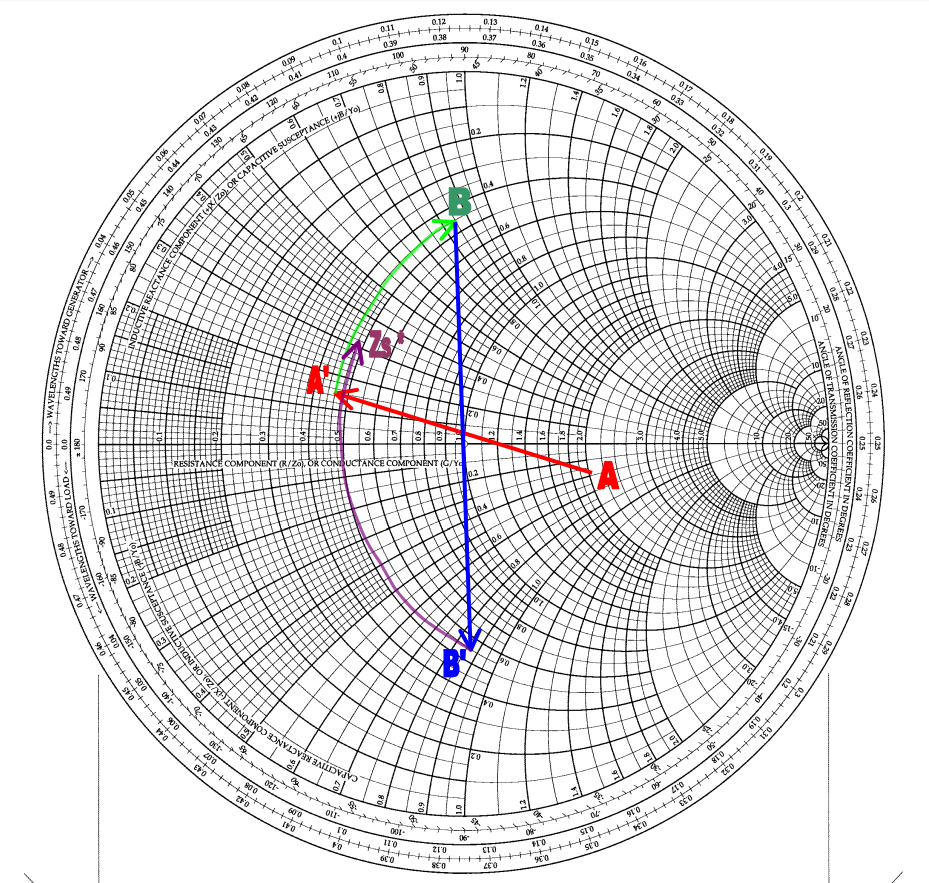
(больший масштаб – в файле PDF)
Найдя точки B и B', мы можем измерить длины дуг A'B и B'D. Первая дает нормированное значение проводимости C. Вторая дает нормированное значение реактивного сопротивления L. Измерение дуги A'B дает b = 0,78 и, следовательно,
\[B = 0,78 \cdot Y_0 = 0,0156 \ См\]
Поскольку ωC = B, то
\[C = \frac{B}{\omega} = \frac{B}{2\pi f} = \frac{ 0,0156 }{ 2 \pi \cdot 60 \cdot 10^6 } = 41,4 \ пФ\]
Дуга B'D, имеет размер x = 1,2, таким образом,
\[X = 1,2 \cdot Z_0 = 60 \ Ом\]
Поскольку ωL = X, то
\[L = \frac{X}{\omega} = \frac{X}{2\pi f} = \frac{ 60 }{2\pi \cdot 60 \cdot 10^6} = 159 \ нГн\]
Второй пример – согласовать выход MAX2472 с сопротивлением нагрузки 50 Ом (Zн) на рабочей частоте 900 МГц (рисунок 14). В этой цепи будет использоваться та же конфигурация, что и в техническом описании MAX2472. На приведенном ниже рисунке 13 показана согласующая цепь с шунтирующей катушкой индуктивности и последовательным конденсатором. Вот как находится решение.

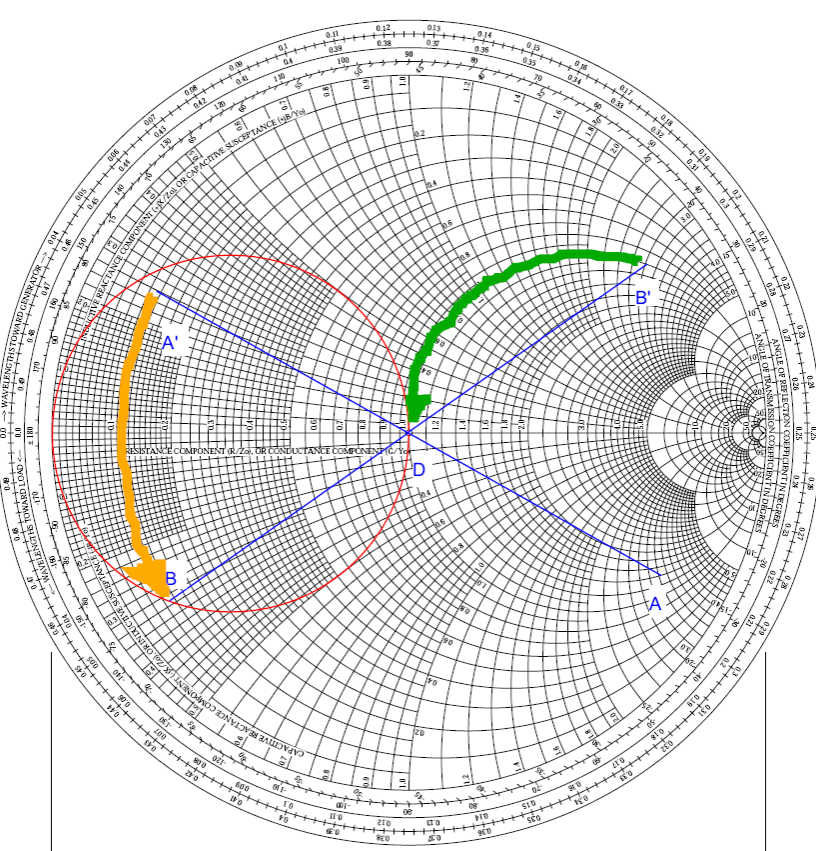
(больший масштаб – в файле PDF)
Первое, что нужно сделать, – это преобразовать параметр рассеяния S22 в его эквивалентное нормализованное полное сопротивление источника. MAX2472 использует Z0 50 Ом. Таким образом, S22 = 0,81/-29,4° становится zи = 1,4 - j3,2, zн = 1 и zн* = 1.
Затем разместим две точки на диаграмме. Отметим A для zи и D для zн*. Поскольку первый элемент, подключенный к источнику, представляет собой шунтирующую катушку индуктивности, преобразуем полное сопротивление источника в полную проводимость. Это дает нам точку А'.
Определим участок дуги, на котором появится следующая точка после подключения индуктивности LMATCH. Поскольку нам неизвестно значение LMATCH, мы не знаем, где остановиться. Однако мы знаем, что после добавления LMATCH (и обратного преобразования в импеданс) результирующий импеданс источника должен лежать на окружности r = 1. Следовательно, дополнительный последовательный конденсатор CMATCH сможет довести результирующий импеданс до z = 1 + j0. Поворачивая окружность r = 1 на 180° вокруг начала координат, мы наносим на график все возможные значения проводимости, соответствующие окружности r = 1. Пересечение этой отраженной окружности и окружности постоянной действительной составляющей проводимости, используемой с точкой A', дает нам точку B (адмиттанс). Отражение точки B на импеданс становится точкой B'.
Найдя точки B и B', мы можем измерить длины дуг A'B и B'D. Первое измерение дает нормированное значение проводимости LMATCH. Второе дает нормированное значение реактивного сопротивления CMATCH. Дуга A'B имеет размер b = -0,575 и, следовательно,
\[B = -0,575 \cdot Y_0 = 0,0115 \ См\]
Поскольку 1/ωL = B, тогда
\[L_{MATCH} = \frac{1}{B \omega} = \frac{1 }{B \cdot 2\pi \cdot f } = \frac{1}{0,01156 \cdot 2 \cdot \pi \cdot 900 \cdot 10^6} = 15,38 \ нГн\]
что округляется до 15 нГн.
Дуга B'D имеет размер x = -2,81, таким образом,
\[X = -2,81 \cdot Z_0 = -140,5 \ Ом\]
Поскольку -1/ωC = X, тогда
\[C_{MATCH} = \frac{-1}{X\omega} = \frac{-1}{X2\pi f} = \frac{ -1}{-140,5 \cdot 2 \cdot \pi \cdot 900 \cdot 10^6} = 1,259 \ пФ\]
что округляется до 1 пФ.
Хотя эти расчетные значения не учитывают паразитные индуктивности и емкости компонентов, они дают значения, близкие к значениям, указанным в техническом описании: LMATCH = 12 нГн и CMATCH = 1 пФ.
Заключение
Учитывая сегодняшнее богатство программного обеспечения и доступность компьютеров, можно усомниться в необходимости такого базового и фундаментального метода расчета базовых схем.
На самом деле, то, что делает инженера настоящим инженером, – это не только академические знания, но и способность использовать для решения задачи ресурсы всех типов. Вставить в программу несколько чисел и заставить ее выдавать решения легко. Когда решения сложны и многогранны, компьютер для выполнения основной работы особенно удобен. Однако знание базовых теории и принципов, которые были перенесены на компьютерные платформы, и откуда они пришли, делает инженера или разработчика более разносторонним и уверенным профессионалом, результаты делает более надежными.
