Понятие t-значений и тестирования на статическую значимость
В данной статье объясняется, как t-значения рассчитываются и используются, чтобы решить, указывают ли экспериментальные данные на взаимосвязь между переменными.
Добро пожаловать в серию статей о роли статистики в электротехнике. Если вы только присоединяетесь к нам, то вы можете найти список тем, которые мы уже рассмотрели, выше в меню с оглавлением серии статей. В противном случае читайте дальше, чтобы узнать, как t-значения могут помочь нам определить, существует ли связь между переменными в экспериментальных данных.
Назначение t-распределения
Если вы читали предыдущую статью, то знаете, что для моделирования нулевой гипотезы с целью оценки статистической значимости мы можем использовать t-распределение вместо нормального распределени. t-распределение полезно, когда мы работаем с небольшим размером выборки, потому что в таких случаях оно дает более точный доверительный интервал.
Форма t-распределения изменяется согласно параметру \(\nu\), который обозначает степени свободы и определяется размером выборки (обозначается n):
\[\nu=n-1\]
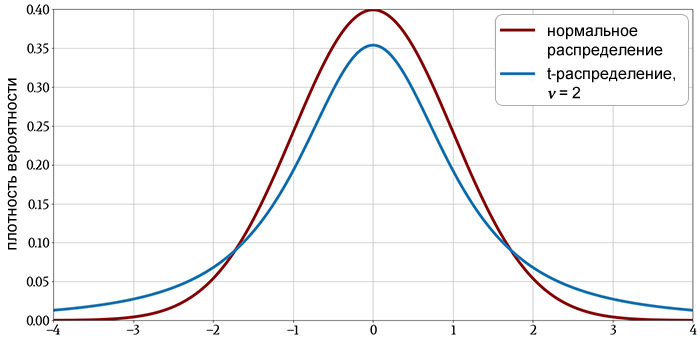
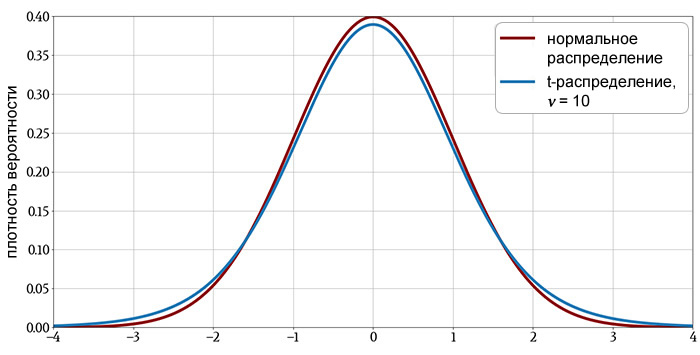
Для небольшого размера выборки t-распределение имеет более тяжелые хвосты, по сравнению с нормальным распределением, что указывает на более высокую вероятность наблюдения значений, далеких от среднего. Для более крупных размеров выборки разница между t-распределением и нормальным распределением становится всё более незначительной.
Эти характеристики очевидны на следующих графиках.
Что такое t-тест?
Когда мы выполняем t-тест, мы используем t-распределение для моделирования нулевой гипотезы. t-тест – это метод оценки статистической значимости путем сравнения средних значений распределений зависимых переменных, наблюдаемых во время эксперимента.
t-тест требует, чтобы независимая переменная была двумерной, то есть имела только два возможных значения. Например, если независимой переменной в эксперименте является температура, мы можем использовать t-тест, если нам нужно проанализировать данные, связанные только с двумя температурами. Если бы мы собирали данные при трех или более температурах, нам нужно было бы использовать другой статистический тест, называемый односторонним дисперсионным анализом (ANOVA, ANalysis Of VAriance).
Как вы, возможно, помните из предыдущей статьи, статистические тесты бывают как параметрическими, так и непараметрическими, а параметрические тесты используются только в том случае, если набор данных демонстрирует достаточную нормальность. t-тест – это параметрический тест. Таким образом, прежде чем применять t-тест, мы должны убедиться, что наши измерения зависимой переменной имеют нормальное распределение.
Кроме того, распределения зависимых переменных, полученные в ходе эксперимента, должны демонстрировать постоянную дисперсию. Другими словами, мы можем применить t-тест, если изменение независимой переменной сдвигает распределение влево или вправо (это эквивалентно изменению среднего), но не, если оно изменяет форму распределения (это было бы эквивалентно изменение дисперсии).
t-значение
При выполнении t-теста мы сравниваем выборочные средние, вычисляя t-значение (также называемое t-статистикой):
\[t=\frac{\bar{x}-\mu}{s/\sqrt{n}}\]
где
- \(\bar{x}\) – выборочное среднее (т. е. среднее измеренных значений зависимой переменной);
- μ – среднее значение генеральной совокупности;
- s – стандартное отклонение выборки, а n - размер выборки.
Во многих экспериментах мы не можем точно знать среднее значение для генеральной совокупности и должны принимать оценочное значение на основе имеющихся данных. В таких случаях, μ более точно определяется как предполагаемое среднее значение для совокупности.
Кроме того, «среднее значение совокупности» может быть просто некоторым другим значением, с которым мы хотим сравнить наблюдения, полученные путем экспериментов. Например, у нас может быть огромное количество данных, показывающих, как система будет работать при одной температуре (возможно, при комнатной температуре).
Значение, соответствующее характеристикам при комнатной температуре, становится средним для генеральной совокупности, а среднее значение по выборке генерируется путем записи ограниченного количества рабочих характеристик, когда система работает в температурной камере при, скажем, 70°C.
Существуют разные типы t-критериев, которые подходят для разных экспериментальных условий. В данной статье мы будем использовать одновыборочный t-тест, который выполняется следующим образом:
- Выберите уровень значимости.
- Найдите критическое значение, соответствующее выбранному уровню значимости и степеням свободы (напомним, что \(\nu = n -1\)). Критические значения для широко используемых уровней значимости легко получить из таблиц, таких как эта; обратите внимание, что «степени свободы» часто сокращенно обозначают как «df» (или «DF»).
- Рассчитайте t-значение, как показано выше, где μ – существующее значение, которое служит точкой сравнения.
- Сравните t-значение с критическим значением. Если величина t-значения больше критического значения, мы отклоняем нулевую гипотезу.
Понятие t-тестов и критических значений
Уровень значимости (например) 0,05 указывает на то, что для того, чтобы отклонить нулевую гипотезу, t-значение должно находиться в той части t-распределения, которая содержит только 5% вероятностной массы. На следующем графике участок, заштрихованный красным, содержит 5% вероятностной массы, а черная вертикальная линия представляет критическое значение.
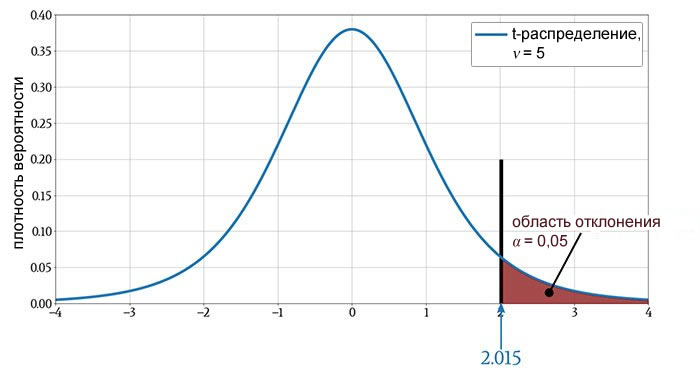
Мыслительный процесс t-теста выглядит примерно так:
- Мы предполагаем, что нулевая гипотеза верна, т.е. что нет никакой связи между независимыми и зависимыми переменными эксперимента.
- Мы сравниваем выборочное среднее значение со средним значением генеральной совокупности, вычисляя t-значение.
- Мы интерпретируем t-значение относительно критического значения, которое зависит от размера выборки и предварительно определенного порога значимости.
- Если величина t-значения больше критического значения (т.е. если оно находится в области отклонения), выборочное среднее настолько далеко от среднего значения генеральной совокупности, что разница, вероятно, не является случайной. Таким образом, мы отвергаем нулевую гипотезу, что эквивалентно утверждению, что эксперимент продемонстрировал связь между независимой переменной и зависимой переменной.
Односторонние и двусторонние тесты
Предыдущая диаграмма соответствует одностороннему t-критерию, что означает, что область отклонения простирается только в одном направлении. Если нас интересует возможность связи, в которой зависимая переменная только увеличивается, мы используем односторонний тест. Мы также используем односторонний тест, если нас интересует возможность связи, в котором зависимая переменная только уменьшается.
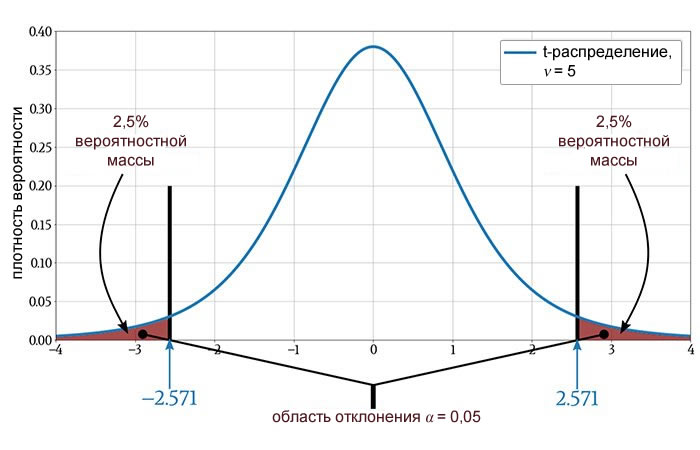
С другой стороны, нас может интересовать как увеличение, так и уменьшение относительно среднего значения генеральной совокупности. Для этого нам нужен двусторонний тест, который разбивает область отклонения на часть выше среднего и часть ниже среднего.
Если мы изменим односторонний тест на двусторонний, мы разделим одну и ту же вероятностную массу на две части, и, следовательно, критическое значение в двустороннем тесте будет отличаться от критического значения в одностороннем тесте.
Следующая диаграмма представляет собой двустороннюю версию условий t-критерия, показанных на предыдущей диаграмме.
Заключение
Мы обсудили, как рассчитать t-значения и как выполнить односторонний t-тест, а также рассмотрели разницу между односторонним и двусторонним тестами. Мы продолжим эту тему в следующей статье, применив наши знания t-теста к примеру эксперимента.
