Что такое последовательно-параллельная цепь?

В простых последовательных цепях все компоненты соединены в цепочку, образуя только один путь для протекания тока:

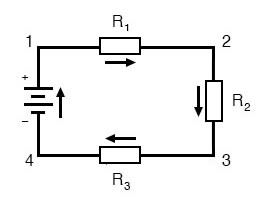
В простых параллельных цепях все компоненты подключаются между одними и теми же двумя наборами электрически общих точек, создавая несколько путей для прохождения тока от одного вывода батареи к другому:

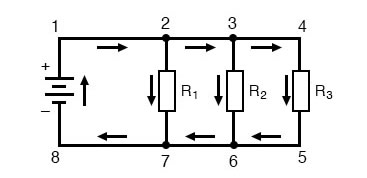
Правила, касающиеся последовательных и параллельных цепей

Для каждой из этих двух основных конфигураций цепей у нас есть определенные наборы правил, описывающих связи для напряжений, токов и сопротивлений.

Последовательные цепи:

• Отдельные падения напряжения в сумме равны общему напряжению.
• Через все компоненты течет один и тот же ток (ток через все компоненты одинаков).
• Сопротивления в сумме равны общему сопротивлению.

Параллельные цепи:

• Напряжение на всех компонентах одинаково (равно).
• Токи ответвлений в сумме равны общему току.
• Сопротивления в итоге дают меньшее общее сопротивление.

Последовательно-параллельные цепи

Однако если компоненты схемы соединены последовательно в одних частях цепи и параллельно в других цепи, мы не сможем применить один набор правил для каждой части этой цепи. Вместо этого нам нужно будет определить, какие части этой цепи являются последовательными, а какие – параллельными, а затем, чтобы определить, что происходит, выборочно применять правила для последовательного и параллельного соединений, по мере необходимости. Возьмем, к примеру, следующую схему:

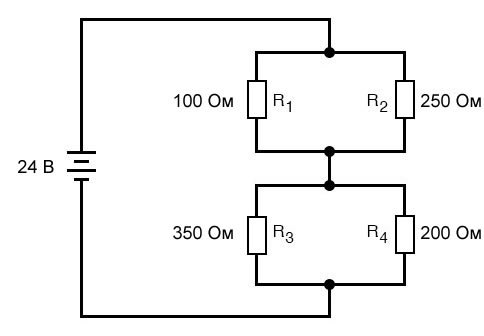
Эта схема не является ни простой последовательной цепью, ни простой параллельной цепью. Скорее, она содержит элементы обоих типов цепей. Ток, выходящий из верхней клеммы батареи, разделяется, чтобы пройти через R₁ и R₂, снова соединяется, затем снова разделяется, чтобы пройти через R₃ и R₄, затем снова соединяется, чтобы вернуться к нижней клемме батареи (поток электронов двигается в противоположном направении). В этой схеме присутствует более одного пути для прохождения тока (следовательно, цепь не последовательная), но в этой схеме также есть более двух наборов электрически общих точек (следовательно, цепь не параллельная).

Поскольку эта схема представляет собой комбинацию последовательной и параллельной цепей, мы не можем применять правила для напряжений, токов и сопротивлений «не глядя», чтобы начать анализ, как мы могли бы сделать, если бы схема принадлежала к одному из этих типов цепей. Например, если бы приведенная выше схема была простой последовательной цепью, мы могли бы просто сложить R₁–R₄, чтобы получить общее сопротивление, вычислить общий ток, а затем вычислить все падения напряжения. Точно так же, если бы приведенная выше схема была простой параллельной цепью, мы могли бы просто вычислить токи ответвлений, сложить токи ответвлений, чтобы вычислить общий ток, а затем вычислить общее сопротивление из общего напряжения и полного тока. Однако решение для этой схемы будет сложнее.

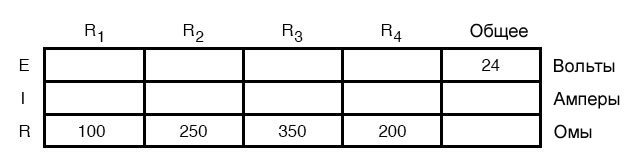
Таблица по-прежнему поможет нам манипулировать различными значениями комбинированных последовательно-параллельных цепей, но мы должны быть осторожны, как и где применять разные правила для последовательного и параллельного соединений. Для определения значений в столбцах таблицы закон Ома, конечно, по-прежнему работает.

Если мы можем определить, какие части схемы являются последовательными, а какие – параллельными, мы можем проанализировать их поэтапно, подходя к каждой части по очереди, используя соответствующие правила для определения связей напряжений, токов и сопротивлений. Остальная часть этой главы будет посвящена демонстрации методик выполнения этой задачи.

Резюме

• К цепям, содержащим оба типа соединений, последовательное и параллельное, правила этих типов цепей должны применяться выборочно.

Теги