Понятие t-распределения в тестах на статистическую значимость
В данной статье представлено статистическое распределение, используемое при проверке значимости. Мы обсудим его важность и связь с нормальным распределением.
Эта статья является продолжением серии статей о статистике в электротехнике. Если вы только присоединяетесь к нам, просмотрите предыдущие статьи этой серии в меню с оглавлением выше.
Краткий обзор статистической значимости
В предыдущей статье была исследована концепция статистической значимости, которая представляет собой широко используемый (хотя и потенциально вводящий в заблуждение) метод определения наличия связи между экспериментальными переменными. Ниже приведено краткое резюме:
- В эксперименте участвуют две (или более) переменные, которые могут быть каким-то образом связаны. Нулевая гипотеза утверждает, что между этими переменными нет никакой связи.
- Обычно мы надеемся, что эксперимент опровергнет нулевую гипотезу. Другими словами, у нас есть основания полагать, что две переменные каким-то образом связаны, и мы планируем эксперимент с целью сбора данных, демонстрирующих наличие связи.
- Мы можем рассчитать вероятность получения наблюдаемого значения, или более экстремального значения, при условии, что нулевая гипотеза верна. Это называется p-значением. Оно передает вероятность получения значения, которое, по крайней мере, столь же экстремально, как наблюдаемое значение, при условии, что между экспериментальными переменными не существует взаимосвязи.
- Статистическая значимость определяется путем сравнения p-значения с заранее определенным порогом, называемым уровнем значимости, обозначенным как ⍺. Широко используемые уровни значимости составляют 1% (⍺ = 0,01) и 5% (⍺ = 0,05).
- Если p-значение меньше уровня значимости, мы вправе отвергнуть нулевую гипотезу. Другими словами, мы можем утверждать, что связь существует, потому что, если бы экспериментальные переменные действительно не были связаны, мы, вероятно, не получили бы наблюдаемого значения.
Моя цель в данной статье – охватить важную информацию о распределении, которое играет важную роль в тестах статистической значимости, а в следующих двух статьях мы обсудим t-значения и проработаем простой пример статистической значимости применительно к инженерно-техническим системам.
t-распределение
Нулевая гипотеза часто принимает форму нормального распределения, потому что это распределение значений создается очень большим количеством явлений, которые находятся под воздействием случайного или чрезвычайно сложного влияния. Однако когда нам действительно нужно вычислить p-значение и сообщить статистическую значимость, мы очень часто используем t-распределение.
t-распределение похоже на нормальное распределение, и по мере увеличения размера выборки оно постепенно становится идентичным нормальному распределению. Термин «t-распределение» на самом деле относится к семейству графиков распределения, поскольку форма графика изменяется в зависимости от размера выборки эксперимента.
В частности, точная форма t-распределения определяется параметром, называемым степенями свободы, который обозначается как \(\nu\) (это строчная греческая буква ню, а не латинская v). Степени свободы равны размеру выборки (обозначается как n) минус один:
\[\nu=n-1\]
Следующие графики показывают t-распределение для различных значений \(\nu\) с графиками нормального распределения, включенными для сравнения.
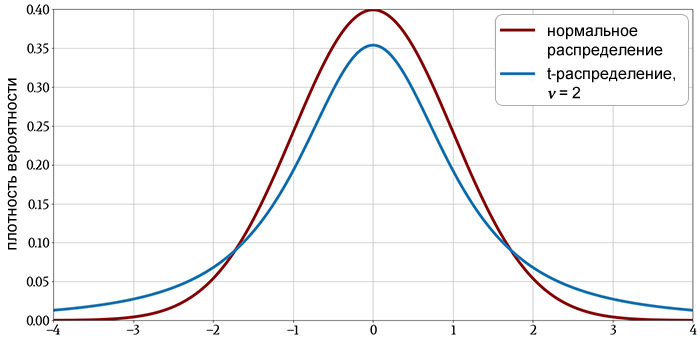
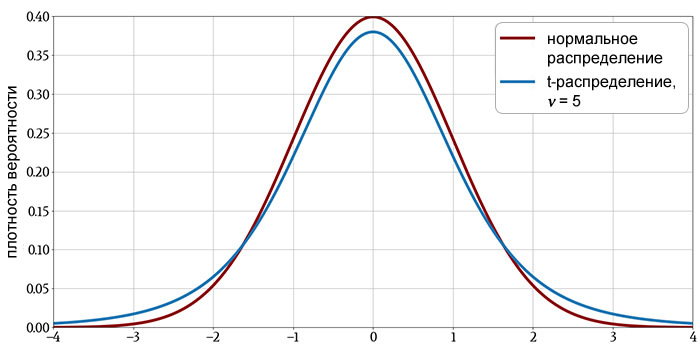
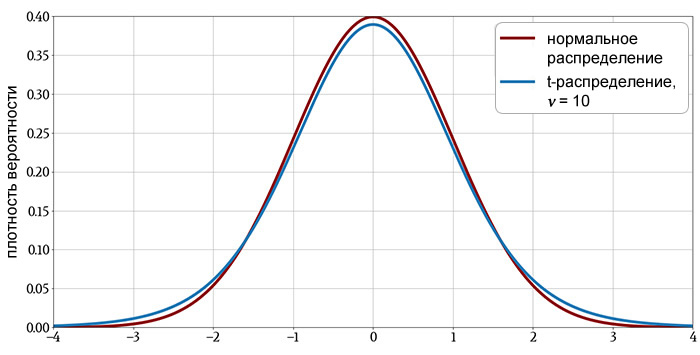
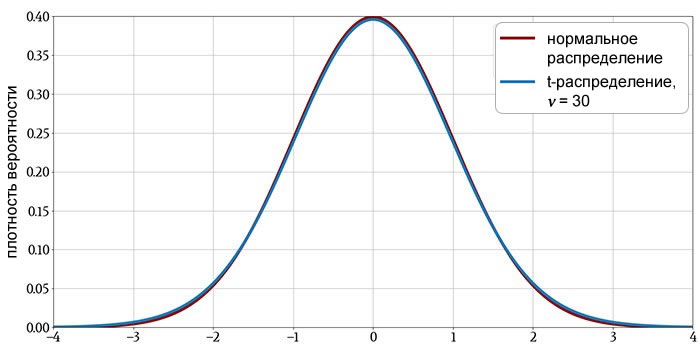
Характеристики t-распределения
t-распределение напоминает стандартное нормальное распределение: его среднее значение равно нулю, оно симметрично относительно среднего, а плотность вероятности уменьшается с той же общей кривизной для значений выше и ниже среднего.
Как вы можете видеть на графиках, t-распределение имеет большую плотность вероятности в хвостах и меньшую в области около пика. Это говорит нам о том, что t-распределение по сравнению с нормальным распределением дает больше значений, далеких от среднего.
Однако эта разница уменьшается с увеличением \(\nu\), указывая на то, что больший размер выборки снижает тенденцию к наблюдению значений, далеких от среднего. Последний график демонстрирует, что когда распределение имеет более примерно 30 степеней свободы, по сути, нет разницы между t-распределением и нормальным распределением.
Происхождение t-распределения
Понятие, которое тесно связано со статистической значимостью, – это доверительный интервал. На следующей диаграмме показан двусторонний 95% доверительный интервал стандартного нормального распределения.
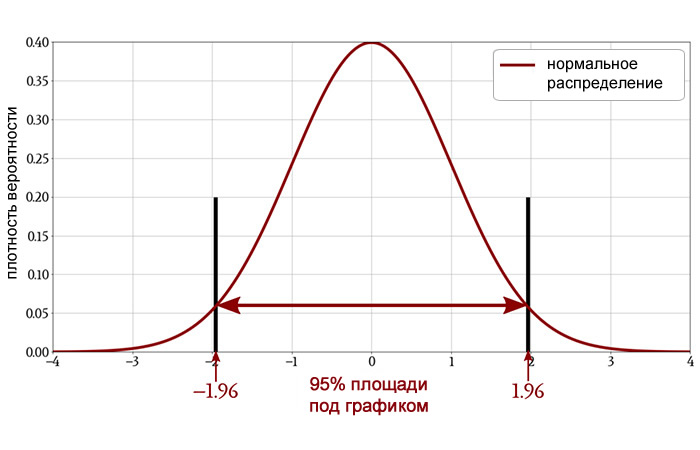
Если среднее значение выборки (то есть среднее значение измерений, которые мы собрали во время эксперимента) попадает в этот доверительный интервал, наблюдаемые значения не являются статистически значимыми при уровне значимости 5%. Среднее значение выборки должно выходить за пределы доверительного интервала, чтобы оправдать отклонение нулевой гипотезы.
Два значения, определяющие доверительный интервал, называются критическими значениями. В случае стандартного нормального распределения критические значения для двустороннего 95% доверительного интервала, который соответствует уровню значимости 5%, составляют –1,96 и +1,96. Если мы выберем другой уровень значимости, критические значения изменятся.
Оказывается, когда размер выборки в эксперименте невелик, доверительный интервал будет слишком узким, если мы моделируем нулевую гипотезу как нормальное распределение. Это означает, что некоторые наблюдаемые значения могут выходить за пределы интервала и, следовательно, предполагать статистическую значимость, когда в действительности результат эксперимента не является статистически значимым.
Почему, когда мы используем нормальное распределение, доверительный интервал слишком узок?
Полное объяснение было бы слишком длинным для этой статьи, но проблема сводится к тому факту, что мы не знаем стандартного отклонения генеральной совокупности и должны использовать вместо этого стандартное отклонение выборки. Стандартное отклонение очень маленькой выборки серьезно недооценивает реальное стандартное отклонение, и мы используем t-распределение, чтобы компенсировать этот эффект.
По мере увеличения размера выборки требуется меньшая компенсация, и поэтому, когда у нас есть больший размер выборки, t-распределение более похоже на нормальное распределение.
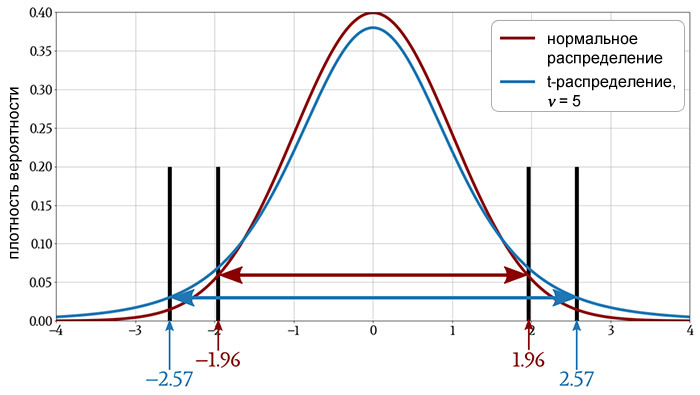
Как вы можете видеть на следующем графике, 95% доверительный интервал становится шире, когда мы используем t-распределение вместо нормального распределения.
Заключение
На данный момент наше обсуждение t-распределения всё еще носит теоретический характер. Я надеюсь, что оно было теоретическим в хорошем смысле, но в любом случае будущие статьи помогут вам понять, как мы претворяем часть этой теории в практику.
