Поиск статистических взаимосвязей: корреляция, причинно-следственная связь и ковариация

В данной статье объясняется статистическая мера, которая помогает нам делать выводы о том, как одна переменная влияет на другую.

В этой серии статей, посвященной статистике в электротехнике, приводятся высокоуровневые определения и примеры статистических концепций, которые можно применять в процессе проектирования. Ознакомиться со статьями серии вы можете в меню с оглавлением выше, над статьей.

Корреляция и причинно-следственная связь

Допустим, у нас есть система беспроводной связи, которая доставляет нам проблемы. Частота битовых ошибок (BER) резко меняется от одного полевого теста к другому, и очевидной причины такого нестабильного поведения нет. Что еще хуже, полевые испытания даже не близки к контролируемым экспериментам, и существует довольно много факторов (тепловые и атмосферные условия, вибрация, радиочастотные помехи, электромагнитные помехи от ближайшего оборудования, ориентация, относительная скорость), которые могут влиять на производительность системы.

Один из способов справиться с этой ситуацией – выбрать факторы, которые с наибольшей вероятностью будут сильно влиять на BER, собрать данные и найти причинно-следственные связи. Поскольку доказать причинно-следственную связь часто очень сложно, наш анализ на самом деле даст количественную оценку корреляции, а затем мы можем либо предположить, что корреляция указывает на причинную связь (что рискованно), либо попытаться продемонстрировать причинность путем сбора новых данных из тщательно спланированного эксперимента.

Таким образом, поиск причинно-следственной связи начинается с поиска корреляции, а корреляция начинается с ковариации.

Переменные, которые изменяются вместе

Описательная статистическая мера, называемая дисперсией, обсуждалась в одной из предыдущих статей, которая также охватывает стандартное отклонение. Дисперсия (обозначается σ²) – это усредненная мощность (выраженная в единицах мощности) случайных отклонений в наборе данных. Мы рассчитываем дисперсию следующим образом:

\[\sigma^2=\frac{1}{N-1}\sum_{i=1}^{N}(X_i-\mu)^2\]

где N – количество значений в наборе данных (т.е. размер выборки), а μ – среднее значение.

Допустим, мы начинаем наше исследование с того, что отправим систему на несколько полевых испытаний и сохраним множество упорядоченных пар, состоящих из значений температуры окружающей среды и BER. Например, мы могли бы вычислить средний BER за пять минут работы, а затем связать эти данные со средней температурой за тот же интервал. Затем мы повторяем процедуру измерения в течение следующего пятиминутного интервала, следующего пятиминутного интервала и так далее.

Данные температуры и BER будут иметь свои собственные отдельные дисперсии, то есть склонность значений в заданном наборе данных отклоняться от среднего значения того же набора данных. Но мы также можем вычислить ковариацию, которая отражает склонность значений в двух наборах данных к линейному изменению вместе (или, более кратко, к линейному совместному изменению, англ. «co-vary» – отсюда и название «ковариация»).

Следующие три графика дают визуальное объяснение того, что означает совместное изменение переменных.

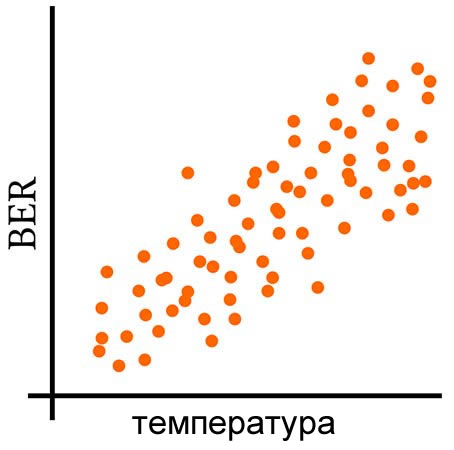
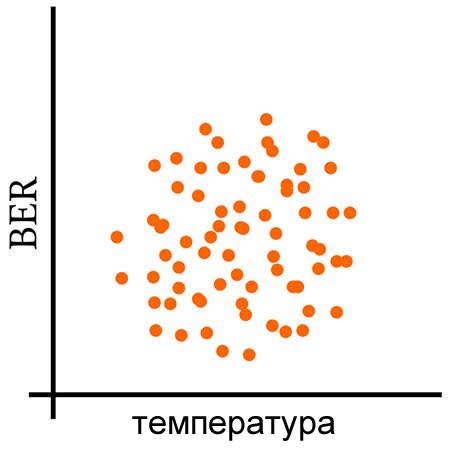
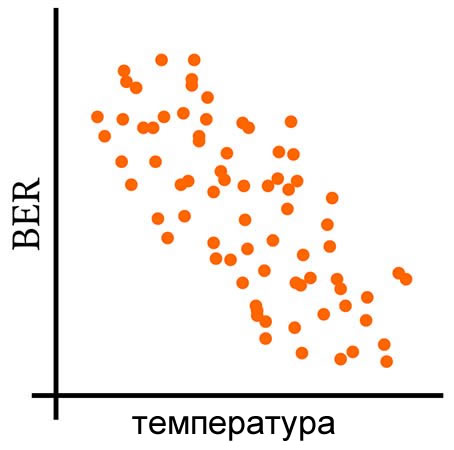
Расчет ковариации

Следующее математическое соотношение определяется как ковариация двух переменных X и Y:

\[\operatorname {cov} (X,Y)=\operatorname {E} {{\big [}(X-\operatorname {E} [X])(Y-\operatorname {E} [Y]){\big ]}}\]

Для дискретных данных с размером выборки N это соотношение будет следующим:

\[\operatorname {cov} (X,Y)=\frac{1}{N-1}\sum_{i=1}^{N}(X_i-\operatorname {E}[X])(Y_i-\operatorname {E}[Y])\]

Возможно, вы не знакомы с обозначением E[X]. «E» означает «ожидаемое значение», которое равно среднему арифметическому. (Существует тонкое концептуальное различие между ожидаемым значением и средним значением, но это тема для другой статьи.) Я хотел ввести это обозначение, потому что концепция ожидаемого значения дает нам другой способ думать о среднем значении набора данных – это значение, которое мы ожидаем от следующего измерения, в том смысле, что это ожидаемое значение имеет наибольшую вероятность появления.

Формула ковариации станет интуитивно понятна, если вы поразмыслите над ней на минуту или две:

• Отклонения (как по величине, так и по полярности) в наборе данных X умножаются на отклонения в наборе данных Y.
• Соответствующие отклонения в двух наборах данных, которые являются как положительными, так и отрицательными, внесут положительный вклад в суммирование.
• Если одно отклонение положительное, а соответствующее отклонение другого набора данных отрицательное, вклад будет отрицательным.
• Когда мы делим результат суммирования на N–1, мы усредняем все эти вклады и тем самым генерируем значение, которое указывает
  • склонность значений в двух наборах данных отклоняться в одном направлении (т.е.положительная ковариация),
  • склонность к отклонениям в противоположные стороны (отрицательная ковариация),
  • или отсутствие склонности к совместному отклонению (нулевая ковариация).

Заключение

Ковариация количественно определяет линейную корреляцию двух случайных величин. Однако значения ковариации несколько сложно интерпретировать, и в следующей статье мы обсудим две модифицированные версии ковариации, которые сделают корреляционный анализ более удобным.

Теги