Описательная статистика в электротехнике
В данной статье рассматриваются статистические методы, которые мы можем использовать для описания характеристик инженерной системы или анализа данных о производительности.
В предыдущей статье была представлена концепция статистического анализа и определены некоторые важные применения статистических методов в области электротехники. В данной статье мы рассмотрим статистические показатели, которые относятся к категории, называемой описательной статистикой.
Важность описательной статистики
Как следует из названия, описательная статистика помогает нам описывать данные. Если кто-то отправит вам список, состоящий только из 172 800 чисел, которые, как кажется, изменяются случайным образом, вы вряд ли получите какую-либо полезную информацию из этих данных. Мы можем улучшить эту ситуацию, предоставив контекст; например: «это температура, по две выборки в секунду, которую система измеряла в течение предыдущих двадцати четырех часов». Теперь вы знаете происхождение и значимость данных, но всё еще крайне сложно провести общую оценку или достичь общего понимания, просматривая, казалось бы, бесконечный список значений.
Вот почему описательная статистика является таким ценным инструментом. Она «суммируют» потенциально огромные объемы данных, извлекая значимые характеристики и передавая общие тенденции. Во многих случаях мы можем сформировать суждение о системе или принять решение о будущей работе над проектом, основываясь только на описательной статистике, – и это хорошо, потому что, кто хотел бы изучать и оценивать 172 800 показаний температуры?
Описательная и аналитическая статистика
Описательная статистика описывает данные. Аналитическая статистика, с другой стороны, помогает нам делать выводы о данных. Простыми словами, вывод – это идея или мнение, которое кто-то формирует, «читая между строк», то есть, анализируя что-то и формируя заключение, которое предполагается, но явно не присутствует в доступной информации.
В статистике мы используем математические процедуры, чтобы вывести значимые соотношения между переменными. Мы можем сделать вывод, основываясь на данных, собранных в лаборатории, что температура окружающей среды от 45°C до 65°C делает микроконтроллер более восприимчивым к сбросам сторожевого таймера. Сам набор данных не содержит этой причинно-следственной связи; набор данных содержит только числа. Связь между температурой и поведением микроконтроллера является выводом, который мы создаем путем анализа чисел.
По моему опыту, аналитическая статистика не особенно распространена при проектировании и характеристике электронных систем. Она более заметна в исследованиях. Примерами методов аналитической статистики являются регрессионный анализ, t-тесты и дисперсионный анализ (ANOVA).
Основы описательной статистики: среднее значение, медиана, мода
Среднее
Статистическое среднее, также называемое средним арифметическим, является одним из способов передачи центральной тенденции в наборе данных. Чтобы вычислить среднее, вы складываете все значения в наборе данных и делите эту сумму на количество значений.
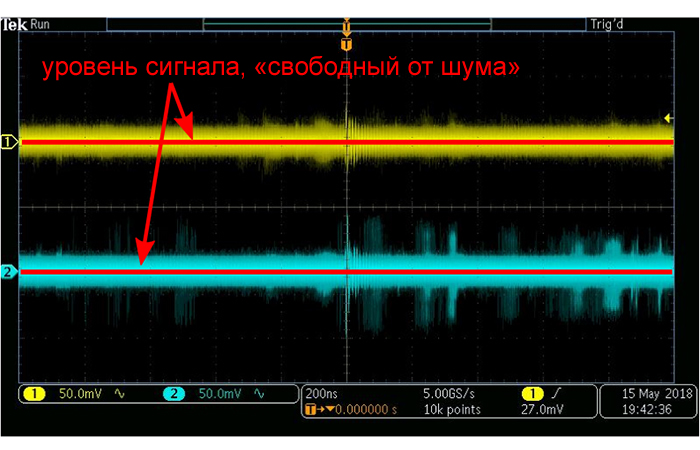
Среднее – это простой способ уменьшить шум в последовательности измерений, поскольку оно аппроксимирует значение, которое будет наблюдаться, если мы устраним небольшие положительные и отрицательные отклонения, вызванные шумом. Мы также можем использовать среднее арифметическое значение для определения смещения сигнала по постоянному напряжению.
Медиана
Чтобы передать информацию о центральной тенденции, мы также можем использовать медиану. Медиана – это значение, которое мы наблюдаем, если взять все точки данных, выстроить их в порядке возрастания и выбрать элемент данных, который делит набор данных на две части одинаковой длины. Я считаю, что среднее более полезно в инженерных приложениях, но медиана имеет важное преимущество: она более устойчива к ложным значениям в наборе данных, тогда как эти ложные значения могут серьезно повлиять на среднее арифметическое.
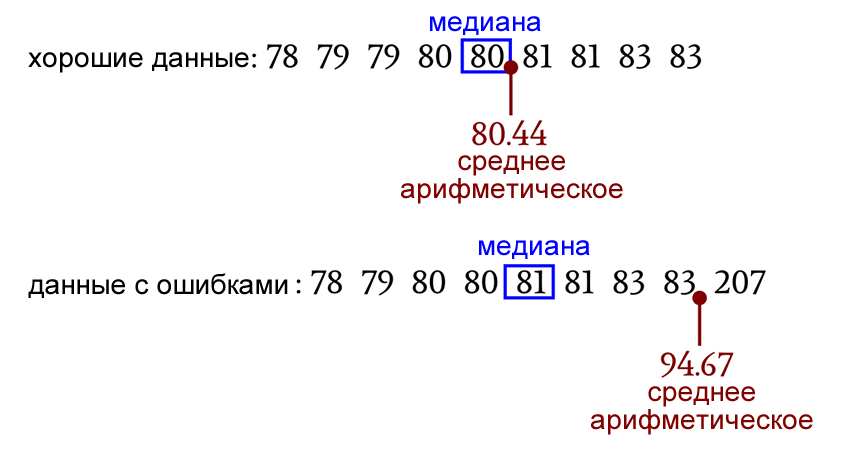
Допустим, у нас есть датчик внешней освещенности, который передает восьмибитные показания через интерфейс UART; он произвел девять измерений освещенности: 80, 81, 83, 79, 78, 81, 83, 80, 79 (единица измерения здесь – люкс). Среднее арифметическое составляет 80,44 люкс, а медиана – 80 люкс. В этом случае обе статистические меры дают точное представление о центральной тенденции в данных.
Однако предположим, что ошибка связи привела к тому, что старший бит последнего измерения интерпретировался как единица, вместо нуля. Это меняет значение с 79 люкс на 207 люкс. Теперь среднее арифметическое значение составляет 94,67 лк, а медиана – 81 лк. Центральная тенденция, передаваемая средним арифметическим значением, стала довольно неточной, но влияние на медиану было незначительным и, вероятно, будет незначительным в большинстве случаев.
Выбросы
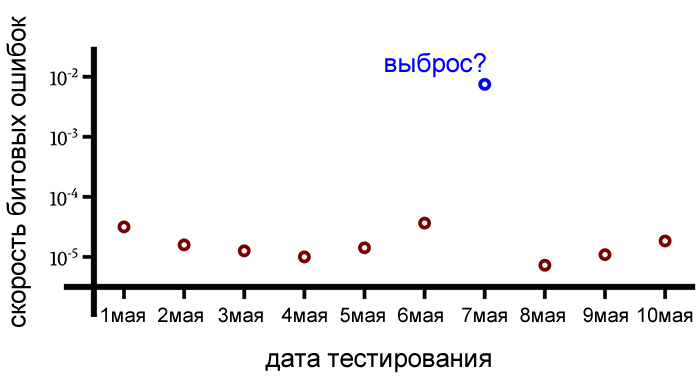
Еще один способ справиться с ложными значениями – это удалить их из набора данных перед вычислением среднего арифметического значения. В статистике ложное значение называется выбросом.
Идентифицировать выбросы нам могут помочь статистические методы, но в целом мы не можем с уверенностью определить, что данный элемент данных является выбросом. Всегда присутствует элемент субъективности, потому что данные – это данные, и если мы решим применить метку «выброс», мы, по сути, говорим элементу: «Ну, вы не принадлежите к этому набору данных, несмотря на факт, что вы на самом деле есть в наборе данных. "
Мода
Значение, которое чаще всего встречается в наборе данных, называется модой. Если мы думаем с точки зрения теории вероятности, мода – это значение, которое мы, скорее всего, получим, если случайным образом выберем какой-либо элемент из набора данных.
Использование моды не часто встречается при описании характеристик электронных систем, и, насколько я знаю, она также не заметна в цифровой обработке сигналов. Честно говоря, я не помню, чтобы когда-либо использовал моду для каких-либо практических целей.
Заключение
Я надеюсь, что это было полезным введением в основную описательную статистику, и что вы четко понимаете разницу между описательной статистикой и аналитической статистикой. Мы продолжим эту тему в следующей статье, в которой обсуждаются дисперсия и стандартное отклонение.
