Как выполнить частотную модуляцию оцифрованным аудиосигналом с помощью Scilab

В данной статье мы будем использовать Scilab для создания частотно-модулированного сигнала, который переносит информацию, соответствующую аудиозаписи.

Вспомогательная информация

• Учимся жить в частотной области (из первой главы миниучебника о радиочастотном анализе и проектировании)
• Частотная модуляция: теория, временная и частотная области

Предыдущие статьи о цифровой обработке сигналов в Scilab

• Основы цифровой обработки сигналов (ЦОС, DSP) для синусоидальных сигналов с Scilab
• Как выполнить анализ в частотной области с помощью Scilab
• Как использовать Scilab для анализа амплитудно-модулированных РЧ сигналов
• Как использовать Scilab для анализа частотно-модулированных РЧ сигналов

В предыдущей статье мы исследовали частотную модуляцию с использованием однородной, одночастотной синусоидальной волны в качестве модулирующего сигнала (сигнала основной полосы). Это вполне разумный способ познакомить вас с этой темой и с основными понятиями, хотя это не очень практично. В большинстве реальных приложений модулирующий сигнал будет представлять собой сигнал сложной формы, которая демонстрирует изменения по частоте и по амплитуде. Эти сложные вариации частоты и амплитуды – это именно то, что мы можем найти в аудиосигналах, и, как вы знаете, частотная модуляция широко используется для передачи звуковой информации.

В данной статье мы преобразуем звуковой файл в типовой массив данных Scilab, а затем выполним частотную модуляцию, используя в качестве модулирующего сигнала основной полосы реальные данные. Это должно быть ценным упражнением для тех, кто интересуется программно-определяемыми радиосистемами (SDR). Когда мы генерируем оцифрованное представление ЧМ сигнала, мы создаем последовательность значений, которые могут быть отправлены на цифро-аналоговый преобразователь, отфильтрованы, усилены и переданны. Это позволяет реализовать специализированную радиочастотную систему без разработки схем модуляции.

Интегрирование модулирующего сигнала основной полосы

Команда Scilab integrate() позволяет нам создать последовательность значений, соответствующих неопределенному интегралу существующей последовательности значений. (Это отличается от определенного интеграла, который просто дает область под кривой от заданной нижней границы до заданной верхней границы.) Начнем с базового синусоидального сигнала:

BufferLength = 2000;
n = 0:(BufferLength - 1);
BasebandFrequency = 5e3;
SamplingFrequency = 1e6;
BasebandSignal = sin(2*%pi*n / (SamplingFrequency/BasebandFrequency));
plot(n, BasebandSignal)

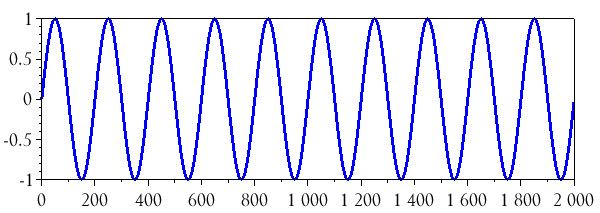
Для команды integrate() требуется четыре аргумента. Первые два являются символьными строками (строки в Scilab заключаются в одиночные или двойные кавычки), третий – это число, а четвертый – последовательность чисел.

• Первый аргумент: функция, которая должна быть интегрирована, такая как ‘f(x) = sin(x)’, но без части ‘f(x) =’.
• Второй аргумент: переменная интегрирования в заданном выражении, указанном в первом аргументе, например, ‘x’.
• Третий аргумент: нижняя граница начала процедуры интегрирования.
• Четвертый аргумент: последовательность значений, которая устанавливает несколько верхних границ интегрирования.

Например:

BasebandSignal_integrated = integrate('sin(2*%pi*n / (SamplingFrequency/BasebandFrequency))', 'n', 0, n);
plot(n, BasebandSignal_integrated)

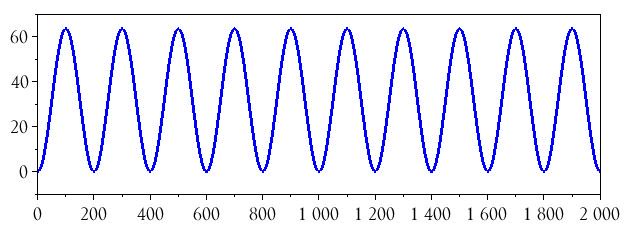
Мы знаем, что интеграл синусоиды представляет собой отрицательную косинусоиду (плюс константу), и команда integrate() действительно создает отрицательную косинусоиду, но имеет смещение по постоянному напряжению, и амплитуда не согласуется с амплитудой исходного сигнала. Эти проблемы легко исправляются. Во-первых, мы устраним смещение по постоянному напряжению, взяв среднее значение всего сигнала и вычитая его из каждого значения в массиве:

BasebandSignal_integrated = BasebandSignal_integrated - mean(BasebandSignal_integrated);
plot(n, BasebandSignal_integrated)

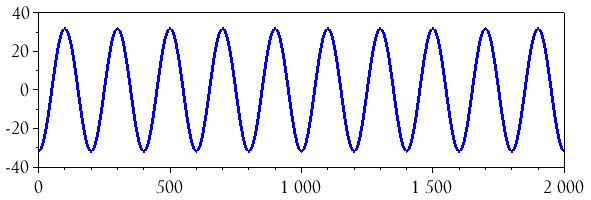
Теперь мы разделим все значения в массиве на максимальное значение:

BasebandSignal_integrated = BasebandSignal_integrated ./ max(BasebandSignal_integrated);
plot(n, BasebandSignal_integrated)

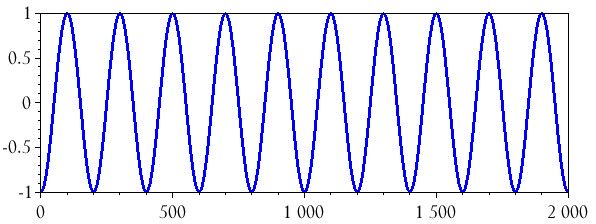
Подключение аудиофайла

Я загрузил mp3 запись человека, произносящего слово «circuit», а затем преобразовал его в WAV файл и загрузил его в Scilab:

audio = wavread("C:\Users\Robert\Downloads\circuit.wav");

Получившийся массив имел более 28000 выборок; я уменьшил его до отрывка из 2000 отсчетов. Также я переставил его содержимое (с помощью оператора '), чтобы он имел размеры 1×2000 вместо 2000×1:

audio = audio(11000:12999);
audio = audio';
plot(n, audio)

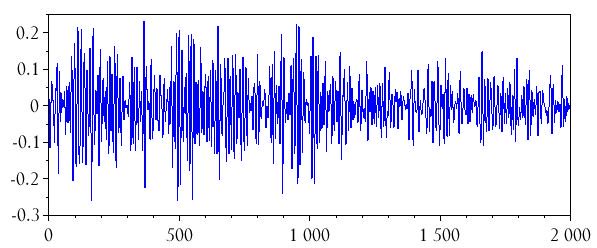
Интегрирование аудиосигнала

Для выполнения интегрирования наших аудиоданных мы будем использовать команду inttrap(). Похоже, что эта процедура математически эквивалентна тому, что мы делали выше с помощью команды integrate(). Причина, по которой я использую inttrap(), заключается в том, что у нас нет возможности (насколько я могу судить) напрямую использовать integrate() с данными, которые не могут быть представлены выражением типа ‘sin(x)’.

Команда inttrap() использует трапециевидную интерполяцию для вычисления определенного интеграла (т.е. области под кривой) формы сигнала, представленного массивом данных. Многократно используя inttrap() с постоянно растущей верхней границей, мы можем создать последовательность определенных интегралов, соответствующую неопределенному интегралу, создаваемому с помощью integrate(). Если вы воспользуетесь этим методом для создания неопределенного интеграла для синусоидального сигнала, то увидите, что результаты соответствуют результатам, полученным с помощью команды integrate().

Вот команды, которые я использовал для интегрирования массива аудиосигнала:

for i=1:2000
  > audio_integrated(i) = inttrap(audio(1:i));
  > end

Теперь удалим смещение по постоянному напряжению (если в сигнале оно имеется) и масштабируем значения в диапазоне от -1 до +1.

audio_integrated = audio_integrated - mean(audio_integrated);
audio_integrated = audio_integrated ./ max(audio_integrated);
plot(n, audio_integrated)

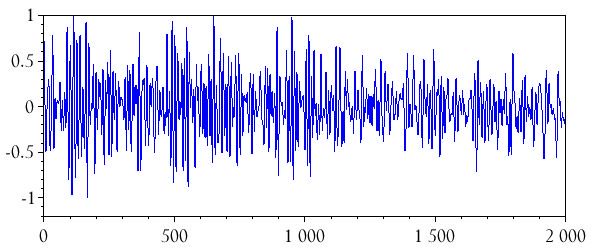
Изменение частоты дискретизации

Перед выполнением модуляции необходимо сделать еще одну вещь. В предыдущей статье мы создали ЧМ сигнал, генерируя синусоидальный сигнал на частоте несущей и включая проинтегрированный модулирующий сигнал основной полосы в качестве дополнительного аргумента фазы. Однако важная деталь заключается в том, что мы использовали частоту дискретизации сигнала основной полосы, которая была достаточно высокой для сигнала несущей частоты. WAV файл, который я использовал в этой статье, имеет частоту дискретизации 44,1 кГц, что означает, что мы не можем использовать частоту дискретизации сигнала основной полосы в процедуре модуляции – частота дискретизации должна быть как минимум в два раза больше самой высокой частоты в модулированном сигнале, и для реалистичной системы вы, вероятно, хотите, чтобы частота дискретизации была как минимум в пять раз больше частоты несущей.

Тогда следующим шагом является увеличение частоты дискретизации проинтегрированного сигнала основной полосы. Мы можем сделать это с помощью команды intdec(). Например, допустим, что несущая частота составляет 800 кГц, и мы решили использовать частоту дискретизации 4,41 МГц. Это означает, что мы изменим массив audio_integrated следующим образом:

SampleRate_IncreaseFactor = 4.41e6 / 44.1e3;
audio_integrated_upsampled = intdec(audio_integrated, SampleRate_IncreaseFactor);

Следующие два графика показывают результаты изменения частоты дискретизации.

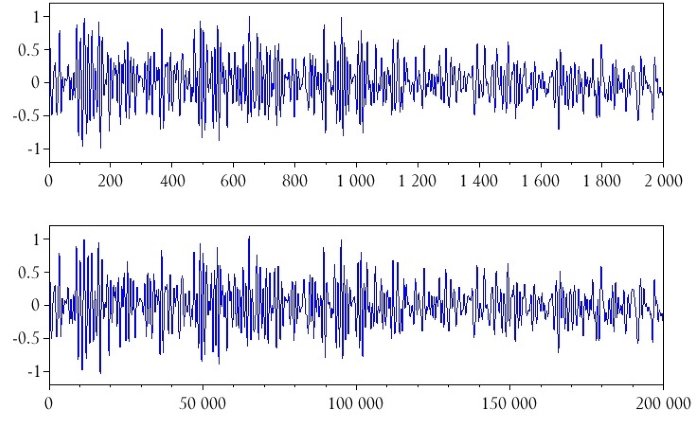
Заключение

На данный момент у нас есть проинтегрированный модулирующий сигнал основной полосы, который готов для команды модуляции, представленной в предыдущей статье. В целом я доволен процедурой, которую здесь разработал, хотя мне интересно, есть ли лучший способ выполнить интегрирование. Если у вас есть предложения, не стесняйтесь делиться своими мыслями в комментариях ниже.

Теги