Цифровая обработка сигналов в Scilab: как декодировать сигнал частотной манипуляции
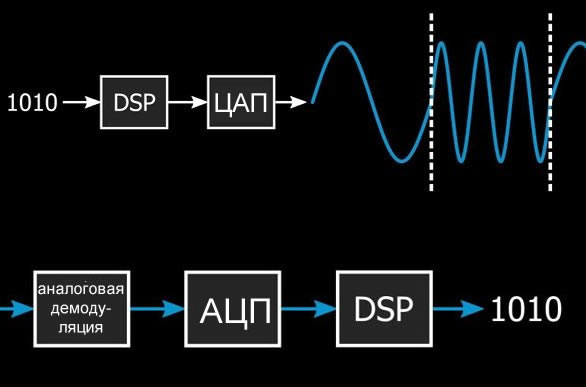
Рассмотрим метод цифровой обработки сигналов, который извлекает исходные цифровые данные из демодулированного сигнала основной полосы частот с частотной манипуляцией (FSK).
Вспомогательная информация
- Цифровая модуляция: амплитуда и частота (из четвертой главы миниучебника о радиочастотном анализе и проектировании)
- Как демодулировать цифровую фазовую модуляцию
Предыдущие статьи о цифровой обработке сигналов в Scilab
- Основы цифровой обработки сигналов (ЦОС, DSP) для синусоидальных сигналов с Scilab
- Как выполнить анализ в частотной области с помощью Scilab
- Как использовать Scilab для анализа амплитудно-модулированных РЧ сигналов
- Как использовать Scilab для анализа частотно-модулированных РЧ сигналов
- Как выполнить частотную модуляцию оцифрованным аудиосигналом с помощью Scilab
- Цифровая обработка сигналов в Scilab: как удалить шум в аудиозаписи с помощью фильтров обработки звука
- Обработка звука в Scilab: как реализовать спектральное вычитание
Один из методов, используемых для кодирования двоичных данных в синусоидальном сигнале, называется частотной манипуляцией (FSK, frequency shift keying). Это простая концепция: одна частота представляет собой ноль, а другая частота представляет собой единицу. Например:
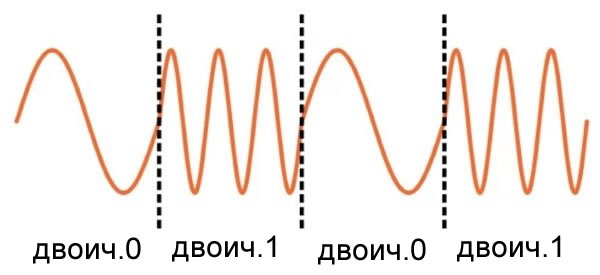
Низкочастотный частотно-манипулированный (FSK) сигнал (скажем, в десятки килогерц) может быть сдвинут на более высокую частоту и затем передан. Это эффективный и довольно простой способ создания радиочастотной системы, которая обеспечивает беспроводную передачу цифровых данных, предполагая, что у нас есть приемник, который может преобразовать все эти синусоидальные сигналы обратно в единицы и нули.
Процесс извлечения цифровых данных из передаваемого FSK сигнала можно разделить на две основные задачи. Во-первых, принятый высокочастотный сигнал преобразуется в низкочастотный сигнал основной полосы частот. Я рассматриваю это как «демодуляцию». Во-вторых, сигнал основной полосы должен быть преобразован в единицы и нули. Я не думаю, что было бы неправильно назвать этот второй шаг «демодуляцией», но чтобы избежать путаницы, я всегда буду использовать термин «декодирование», когда буду говорить о преобразовании низкочастотных аналоговых сигналов в цифровые биты.
Программное декодирование
Для систем со средними скоростями передачи данных вполне возможно оцифровать FSK сигнал основной полосы и выполнять декодирование программно. (Для получения дополнительной информации о радиочастотных системах, которые выполняют важные задачи обработки сигналов в программном обеспечении, вы можете ознакомиться с нашим введением в программно определяемые радиосистемы.) На мой взгляд, это отличный подход, потому что он позволяет приемнику пользоваться преимуществами универсальности цифровой обработки сигналов, а также обеспечивает удобный способ записи и анализа полученных сигналов во время тестирования.
В данной статье мы будем использовать Scilab для декодирования сигнала частотной манипуляции, но соответствующие вычисления не являются сложными и могут быть легко реализованы как C-код в цифровом сигнальном процессоре.
Сперва математика
Наша методика декодирования частотной манипуляции основана на умножении синусоидальных сигналов. Рассмотрим следующие тригонометрические тождества:
\[\sin(x) \cdot \sin(y)=\frac{1}{2}(\cos(x-y)-\cos(x+y))\]
\[\cos(x) \cdot \cos(y)=\frac{1}{2}(\cos(x-y)+\cos(x+y))\]
Давайте сделаем это более согласованным с инженерным миром, используя ω1t и ω2t вместо x и y.
\[\sin(\omega_1t) \cdot \sin(\omega_2t)=\frac{1}{2}(\cos((\omega_1-\omega_2)t)-\cos((\omega_1+\omega_2)t))\]
\[\cos(\omega_1t) \cdot \cos(\omega_2t)=\frac{1}{2}(\cos((\omega_1-\omega_2)t)+\cos((\omega_1+\omega_2)t))\]
(Обратите внимание, что мы игнорируем влияние разностей фаз, в этой статье мы предполагаем, что все сигналы имеют одинаковую фазу.) Мы можем умножать два синусоидальных сигнала или два косинусоидальных сигнала, и результат будет состоять из двух косинусоидальных сигналов с частотами равными, сумме и разности двух исходных частот. Критическое наблюдение здесь состоит в том, что сигнал cos((ω1–ω2)t) будет иметь очень низкую частоту, если два входных сигнала имеют очень схожие частоты. В идеализированной математической реальности мы могли бы ввести два сигнала с одинаковыми частотами, cos((ω1–ω2)t) стал бы cos(0t) = cos(0) = 1. Таким образом, если мы умножим два синусоидальных сигнала или два косинусоидальных сигнала, равных по частоте, результирующий сигнал будет иметь относительно большое смещение по постоянному напряжению.
В контексте декодирования частотной манипуляции (FSK) можно сказать следующее. Даже если частоты схожи, а не идентичны, по-прежнему будет большое смещение по постоянному напряжению, потому что сигнал cos((ω1–ω2)t) будет начинаться с 1 и за продолжительность одного бита будет уменьшаться относительно очень медленно. Продолжительность бита – это время, необходимое для кодирования одного цифрового бита; на диаграмме выше, длительность бита соответствует одному периоду частоты логического нуля (или трем периодам частоты логической единицы). Фрагмент аналогового сигнала, который содержится в одной продолжительности бита, называется символом. В данной статье мы используем двоичную (то есть двухчастотную) частотную манипуляцию (FSK), и, следовательно, один символ соответствует одному цифровому биту. Можно использовать более двух частот, в этом случае один символ будет передавать несколько бит.
Декодирование частотной манипуляции (FSK), шаг за шагом
Теперь у нас есть информация, необходимая для формулировки процедуры декодирования частотной манипуляции:
- Оцифровать полученный сигнал основной полосы частот.
- Определить начало продолжительности бита. Это может быть выполнено с помощью тренировочной/синхронизирующей последовательности; для получения дополнительной информации смотрите подраздел «Преамбула» раздела «Анатомия пакета» в этой статье. Для данной статьи мы будем предполагать, что данные были закодированы как синусоидальные волны (как показано на диаграмме выше), а не как косинусоидальные волны.
- Умножить каждый символ на синусоидальную волну с частотой логического 0 и на синусоидальную волну с частотой логической 1.
- Вычислить смещение по постоянному напряжению каждого символа.
- Выбрать пороговое значение и сделать выбор между логическими 0 и 1 на основании того, является ли смещение символа по постоянному напряжению выше или ниже порогового значения.
Реализация Scilab
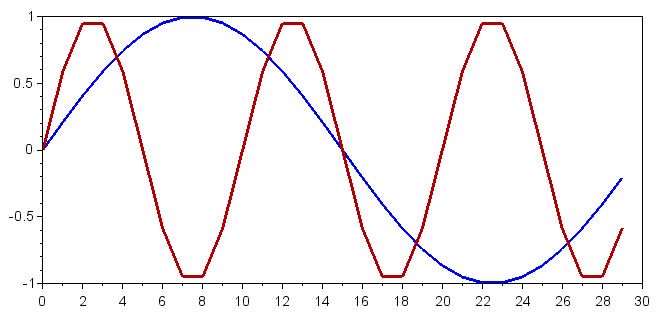
Мы начнем с создания односимвольных синусоидальных сигналов на частоте логического 0 (10 кГц) и частоте логической 1 (30 кГц).
ZeroFrequency = 10e3;
OneFrequency = 30e3;
SamplingFrequency = 300e3;
Samples_per_Symbol = SamplingFrequency/ZeroFrequency;
n = 0:(Samples_per_Symbol-1);
Symbol_Zero = sin(2*%pi*n / (SamplingFrequency/ZeroFrequency));
Symbol_One = sin(2*%pi*n / (SamplingFrequency/OneFrequency));
plot(n, Symbol_Zero)
plot(n, Symbol_One)
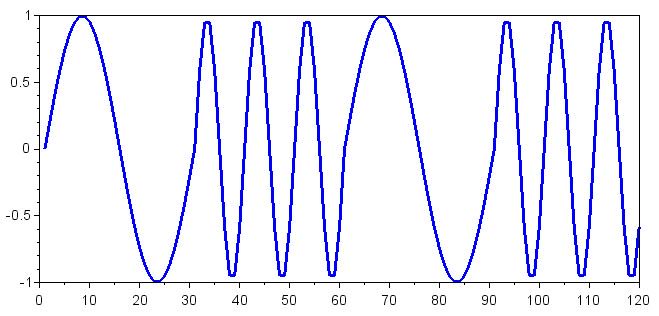
Теперь давайте создадим принятый сигнал основной полосы частот. Мы можем сделать это, объединив массивы Symbol_Zero и Symbol_One; мы будем использовать последовательность 0101:
ReceivedSignal = [Symbol_Zero Symbol_One Symbol_Zero Symbol_One];
plot(ReceivedSignal)
Затем мы умножаем каждый символ в принятом сигнале на символ логического 0 и на символ логической 1. Мы выполняем этот шаг, увеличивая массивы Symbol_Zero и Symbol_One в соответствии с количеством символов в принятом сигнале, а затем используя поэлементное умножение (для дополнительной информации о поэлементном умножении в Scilab смотрите эту статью).
Decoding_Zero = ReceivedSignal .* [Symbol_Zero Symbol_Zero Symbol_Zero Symbol_Zero];
Decoding_One = ReceivedSignal .* [Symbol_One Symbol_One Symbol_One Symbol_One];
plot(Decoding_Zero)
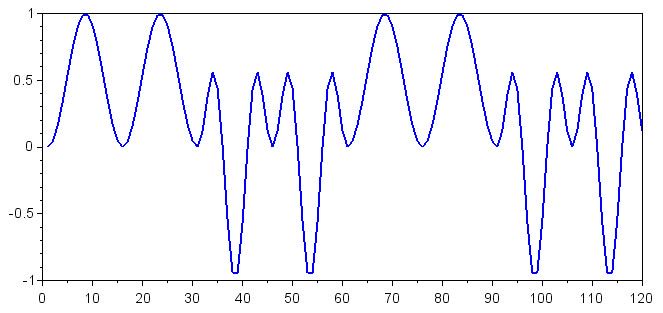
plot(Decoding_One)
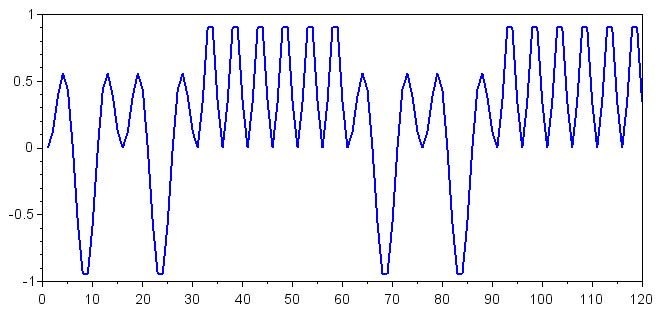
Не отвлекайтесь на эти сигналы довольно сложной формы; всё, что нас интересует, это смещение по постоянному напряжению, которое в математических терминах является просто средним значением. Если мы хотим отобразить смещение по постоянному напряжению, соответствующее каждому символу, сначала нужно создать несколько новых массивов:
for k=1:(length(Decoding_Zero)/Samples_per_Symbol)
> SymbolOffsets_Zero(((k-1)*Samples_per_Symbol)+1:k*(Samples_per_Symbol)) = mean(Decoding_Zero(((k-1)*Samples_per_Symbol)+1:k*(Samples_per_Symbol)));
> end
for k=1:(length(Decoding_One)/Samples_per_Symbol)
> SymbolOffsets_One(((k-1)*Samples_per_Symbol)+1:k*(Samples_per_Symbol)) = mean(Decoding_One(((k-1)*Samples_per_Symbol)+1:k*(Samples_per_Symbol)));
> end
Возможно, вам придется немного поразмыслить над этими командами, чтобы точно понять, что я делаю, но вот основная идея. Цикл for используется для прогона по одному символу за один раз через массивы Decoding_Zero и Decoding_One. В массивах SymbolOffsets_Zero и SymbolOffsets_One все точки данных, соответствующие одному символу, заполняются средним значением соответствующего символа в массивах Decoding_Zero и Decoding_One. У нас есть 30 выборок на символ, поэтому первая команда работает со значениями массива от 1 до 30, следующая работает со значениями массива от 31 до 60, и так далее. Вот результаты:
plot(SymbolOffsets_Zero)
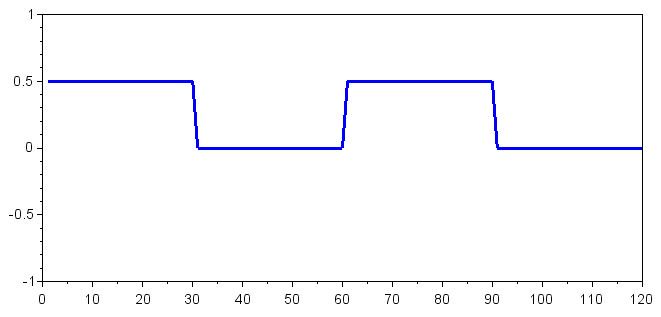
plot(SymbolOffsets_One)
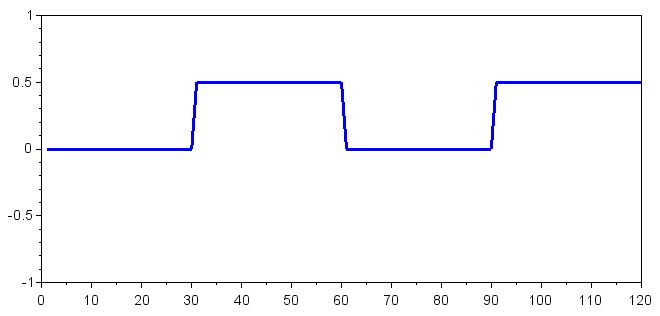
Массив SymbolOffsets_Zero показывает нам смещение по постоянному напряжению, возникающее в результате умножения принятого символа в основной полосе на частоту двоичного нуля, а массив SymbolOffsets_One показывает нам смещение по постоянному напряжению, возникающее в результате умножения принятого символа в основной полосе на частоту двоичной единицы. Мы знаем, что умножение двух одинаковых частот приведет к относительно большому смещению по постоянному напряжению. Таким образом, значение 0,5 в массиве SymbolOffsets_Zero указывает, что принятый символ был двоичным 0, а значение 0,5 в массиве SymbolOffsets_One указывает, что принятый символ был двоичной 1.
Заключение
В данной статье представлен математический подход для декодирования частотной манипуляции (FSK). Процедура была реализована в Scilab, но команды Scilab нетрудно перевести на язык программирования высокого уровня, такой как C. В следующей статье мы продолжим работу с декодированием FSK.
