Как использовать Scilab для анализа частотно-модулированных РЧ сигналов
Вычисление дискретного преобразования Фурье может помочь вам проанализировать, как радиочастотная модуляция влияет на спектр сигнала несущей.
Вспомогательная информация
- Учимся жить в частотной области (из первой главы миниучебника о радиочастотном анализе и проектировании)
- Множество типов радиочастотной модуляции (и другие страницы из главы 4 миниучебника)
Предыдущие статьи о цифровой обработке сигналов в Scilab
- Основы цифровой обработки сигналов (ЦОС, DSP) для синусоидальных сигналов с Scilab
- Как выполнить анализ в частотной области с помощью Scilab
- Как использовать Scilab для анализа амплитудно-модулированных РЧ сигналов
Влияния амплитудной модуляции в частотной области достаточно просты: основной математической операцией в АМ системах является умножение, а умножение заставляет спектр смещаться так, что оно центрируется относительно новой частоты. Математическое соотношение, составляющее основу частотной модуляции, сложнее:
\[x_{АМ}(t)=\sin(\omega_{нес}t+\int_{-\infty}^{t} x_{нч}(t)dt)\]
Как вы можете видеть, частотно-модулированный сигнал создается путем добавления интеграла от модулирующего сигнала к аргументу функции синуса, которая соответствует несущей. Другими словами, несущая – это sin(ωнесt), что означает, что синусоидальный сигнал с угловой частотой ωнес и без аргумента фазы, а ЧМ сигнал – это несущая с добавлением изменяющегося во времени фазового аргумента, равного интегрированному низкочастотному модулирующему сигналу.
С частотной модуляцией тесно связана фазовая модуляция:
\[x_{ФМ}(t)=\sin(\omega_{нес}t+x_{нч}(t))\]
Таким образом, если вы хотите проанализировать промодулированный по фазе сигнал, то почти всё в данной статье применимо к этому. Всё, что вам нужно сделать, это использовать низкочастотный модулирующий сигнал, а не его интеграл, в качестве изменяющегося во времени фазового аргумента.
Интегрирование модулирующего сигнала основной полосы
Начнем с создания массивов низкочастотного модулирующего сигнала и сигнала несущей. Обратите внимание, что частота дискретизации и длина буфера увеличены в десять раз по сравнению с тем, что мы использовали в предыдущей статье; я сделал это, потому что хотел, чтобы более высокочастотные участки модулированного сигнала имели больше выборок за период.
BasebandFrequency = 10e3;
CarrierFrequency = 100e3;
SamplingFrequency = 1e7;
BufferLength = 2000;
n = 0:(BufferLength - 1);
BasebandSignal = sin(2*%pi*n / (SamplingFrequency/BasebandFrequency));
CarrierSignal = sin(2*%pi*n / (SamplingFrequency/CarrierFrequency));
plot(n, BasebandSignal)
plot(n, CarrierSignal)
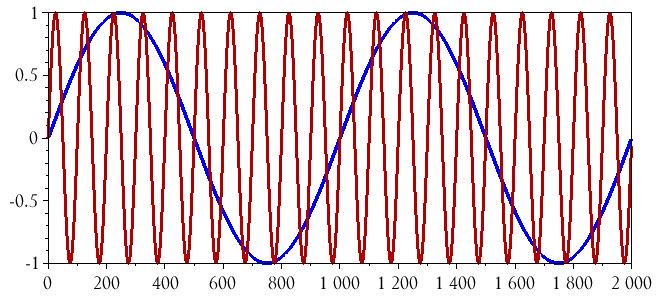
Теперь нам нужно интегрировать сигнал основной полосы. Вычисление неопределенного интеграла оцифрованного сигнала не является особенно простым. В Scilab есть команда integrate(), которая может помочь нам с этой задачей, integrate() – это тема для отдельной статьи, поэтому в этой статье я собираюсь использовать более простой метод и обсудить использование integrate() в следующей статье.
Более простой метод, который мы будем использовать сейчас, основан на следующих наблюдениях:
- Сигнал основной полосы представляет собой постоянную, одночастотную синусоиду.
- Неопределенный интеграл синусоиды представляет собой отрицательную косинусоиду (плюс константа, в нашем случае константа равна нулю).
Итак, всё, что нам нужно сделать, это изменить команду BasebandSignal = sin(...) на BasebandSignal_integral = –cos(...):
BasebandSignal_integral = -cos(2*%pi*n / (SamplingFrequency/BasebandFrequency));
plot(n, BasebandSignal)
plot(n, BasebandSignal_integral)
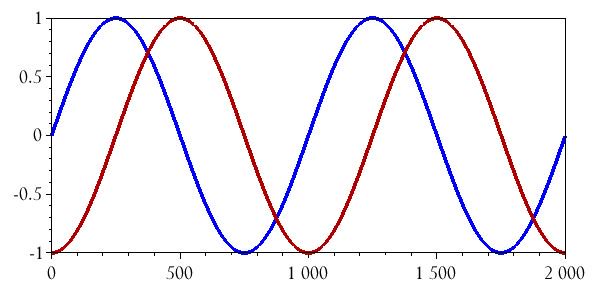
Частотная модуляция во временной области
Теперь мы готовы сгенерировать ЧМ сигнал. Всё, что нам нужно сделать, это взять команду, используемую для создания сигнала несущей, и добавить массив BasebandSignal_integral к аргументу функции sin().
ModulatedSignal_FM = sin((2*%pi*n / (SamplingFrequency/CarrierFrequency)) + BasebandSignal_integral);
Ниже показан результат.
plot(n, ModulatedSignal_FM)
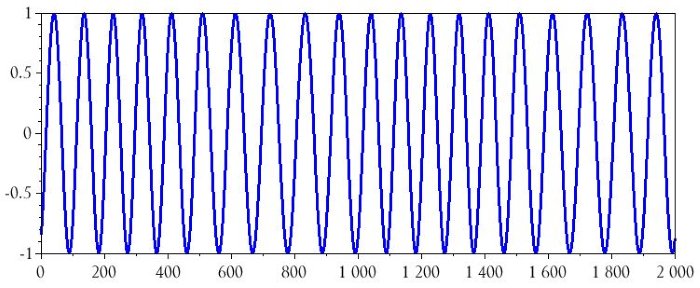
Не волнуйтесь, частотная модуляция там где-то есть. Проблема в том, что вы не можете ее увидеть, потому что изменения частоты слишком малы относительно несущей частоты. Здесь вводится индекс модуляции. Индекс модуляции, обозначенный символом m, используется для увеличения (или уменьшения) величины изменения частоты, вызванного заданным значением модулирующего сигнала:
\[x_{ЧМ}(t)=\sin(\omega_{нес}t+m\int_{-\infty}^{t} x_{нч}(t)dt)\]
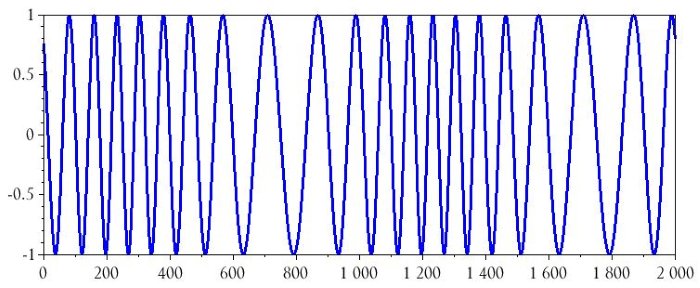
Если мы включим индекс модуляции 4 в команду, используемую для генерации данных ЧМ, эффект модуляции будет гораздо более очевидным:
ModulatedSignal_FM = sin((2*%pi*n / (SamplingFrequency/CarrierFrequency)) + (4*BasebandSignal_integral));
plot(n, ModulatedSignal_FM)
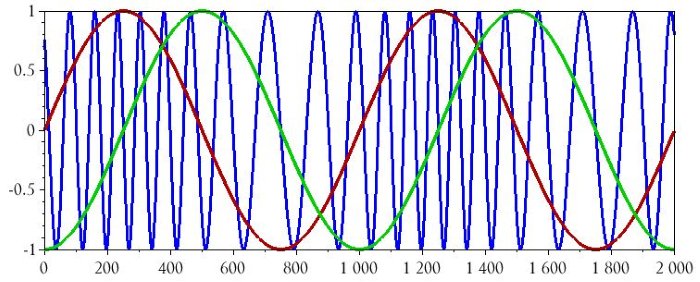
Мы можем добавить на график исходный модулирующий сигнал и проинтегрированный модулирующий сигнал, на всякий случай, если вы захотите увидеть взаимосвязь между этими двумя сигналами и частотно-модулированным сигналом.
plot(n, BasebandSignal)
plot(n, BasebandSignal_integral)
Частотная модуляция в частотной области
Следующие команды создадут представление частотно-модулированного сигнала в частотной области.
HalfBufferLength = BufferLength/2;
HorizAxisIncrement = (SamplingFrequency/2)/HalfBufferLength;
DFTHorizAxis = 0:HorizAxisIncrement:((SamplingFrequency/2)-HorizAxisIncrement);
FM_DFT = fft(ModulatedSignal_FM);
FM_DFT_magnitude = abs(FM_DFT);
plot(DFTHorizAxis, FM_DFT_magnitude(1:HalfBufferLength))
xlabel("Frequency (Hz)")
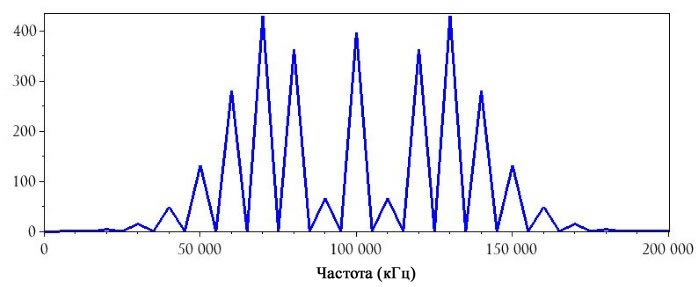
Здесь есть две особенности, которые я хочу упомянуть. Во-первых, амплитуда боковой полосы может быть выше амплитуды компонента на несущей частоте. Во-вторых, полоса частот модулированного сигнала (около ±70 кГц относительно несущей частоты) намного больше, чем ширина полосы частот модулирующего сигнала (т.е. ±10 кГц).
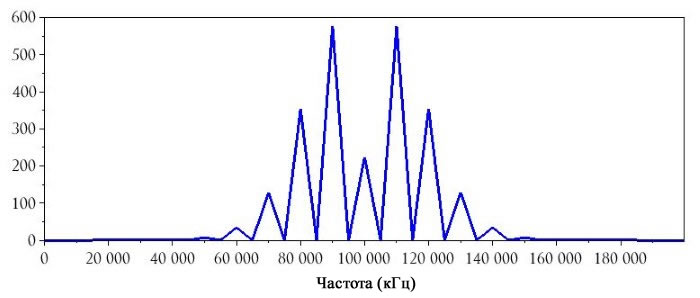
Однако важно понимать, что указанные выше особенности не обязательны для всех случаев частотной модуляции. На характеристики спектра ЧМ сигнала влияют различные факторы; например, если мы понизим индекс модуляции до 2, то получим следующее:
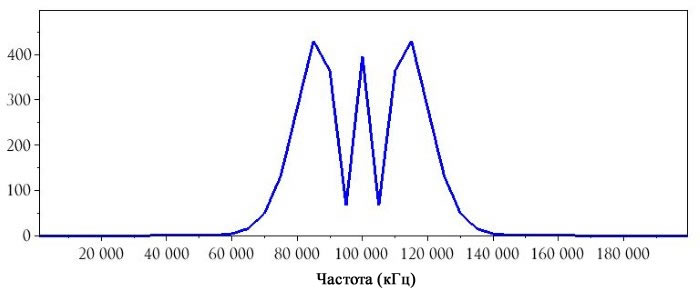
Если мы вернем индекс модуляции 4 и уменьшим частоту модулирующего сигнала в 2 раза, спектр изменится на следующий:
Заключение
Я не изучал интенсивно частотную модуляцию с точки зрения теоретического анализа, но, насколько я могу судить, довольно сложно предсказать характеристики спектра ЧМ сигнала на основе математических соотношений между модулирующим сигналом и сигналом несущей. Это отличная причина использовать Scilab (или MATLAB, или Octave) для частотного анализа ЧМ систем. Я надеюсь, данная статья предоставила хорошее представление, и мы продолжим обсуждение в следующей статье.
