Учимся жить в частотной области
Что такое частотная область? И почему она так важна для радиочастотного проектирования, анализа и тестирования?
Возможно, один из самых фундаментальных шагов в процессе получения знаний в области радиочастотного проектирования – это научиться думать в частотной области. Для большинства из нас бо́льшая часть нашего раннего опыта работы с электрическими цепями и сигналами остается в контексте напряжений и токов, которые являются либо постоянными, либо изменяющимися во времени. Например, когда мы измеряем напряжение батареи с помощью мультиметра, у нас есть постоянная величина, а когда мы смотрим синусоидальное напряжение на осциллографе, мы имеем величину, изменяющуюся во времени.
Радиоволны, с другой стороны, представляют собой мир частот. Мы не посылаем на антенны постоянные напряжения, и осциллограф обычно не эффективен для захвата и визуализации типов манипуляций с сигналами, которые используются в беспроводной связи. На самом деле можно сказать, что временная область – это просто неудобное место для проектирования и анализа радиочастотных систем. Нам необходима другая парадигма.
Фурье
Преобразование Фурье представляет собой математический путь, который ведет к этой альтернативной парадигме, поскольку он обеспечивает точный метод описания сигнала в соответствии с его частотным содержимым.
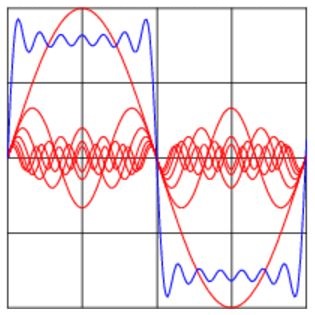
В контексте радиочастот преобразование Фурье может принимать чрезвычайно сложные изменения сигнала и преобразовывать их в компоненты в частотной области, которые являются гораздо более информативными, чем исходная форма сигнала во временной области.
Подробности, связанные с преобразованием Фурье или дискретным преобразованием Фурье (ДПФ, DFT), не тривиальны; однако об этом сейчас беспокоиться не стоит. Вы можете понимать и использовать методы частотной области, даже если очень мало знаете об основных математических операциях.
Преобразование Фурье создает выражения, которые показывают частотное содержимое сигнала, а ДПФ выдает соответствующие числовые данные. Однако в контексте практической инженерии графическое представление часто намного удобнее. В конечном счете, эти графики в частотной области становятся такими же обычными и интуитивными, как диаграмма на осциллографе.
Спектр
Диаграмма в частотной области называется спектром. Идеализированный спектр синусоиды 1 МГц выглядит так:
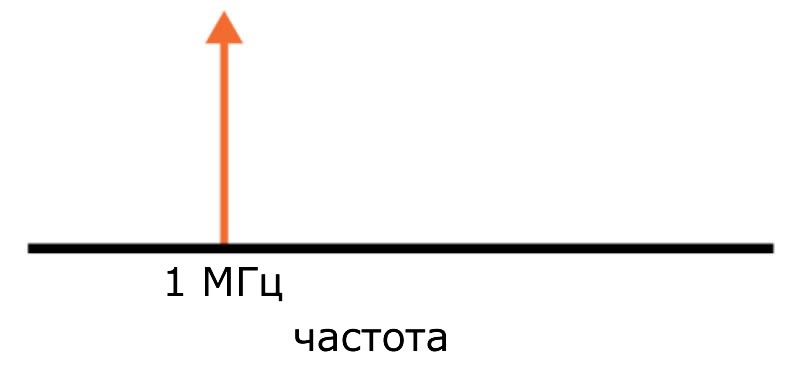
Вертикальная стрелка указывает, что на частоте 1 МГц присутствует определенное количество «энергии». Линейная часть стрелки настолько тонкая потому, что этот идеализированный сигнал не имеет абсолютно никаких других частотных составляющих – вся энергия сконцентрирована точно на 1 МГц.
Если бы мы использовали схему суммирования для объединения этой идеальной синусоиды 1 МГц с идеальной синусоидой 2 МГц, спектр выглядел бы так:

Этот график в частотной области дает очень четкие данные о частотных характеристиках нашего нового сигнала. Если вас в первую очередь интересует поведение вашей схемы не относительно произвольного момента (во временной области), а в контексте частот (в частотной области), спектр даст вам всю необходимую информацию. График во временной области, напротив, будет сложным:
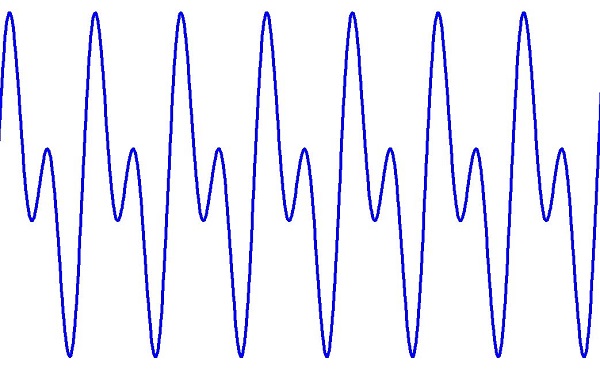
Гораздо менее очевидно, что эта осциллограмма является результатом добавления одной синусоиды с частотой f ко второй синусоиде с частотой 2f.
Идеал и реальность
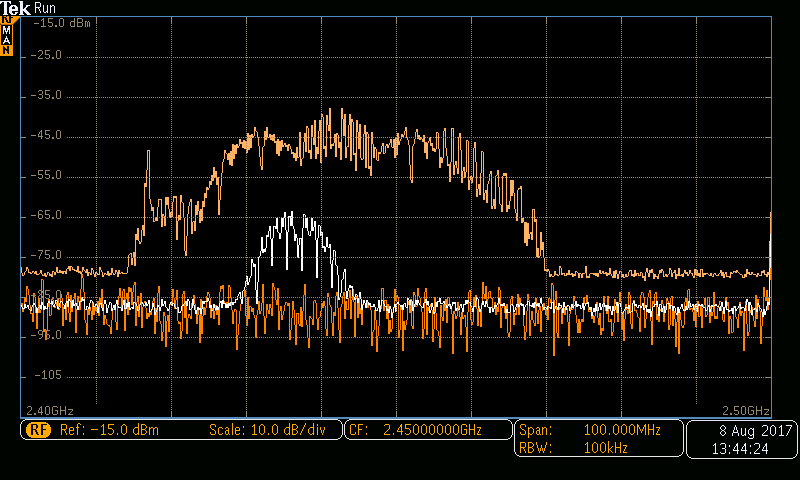
Представленные выше частотные компоненты, показанные в виде тонких вертикальных линий, являются математическими конструкциями; реальные измерения спектра выглядят примерно так:
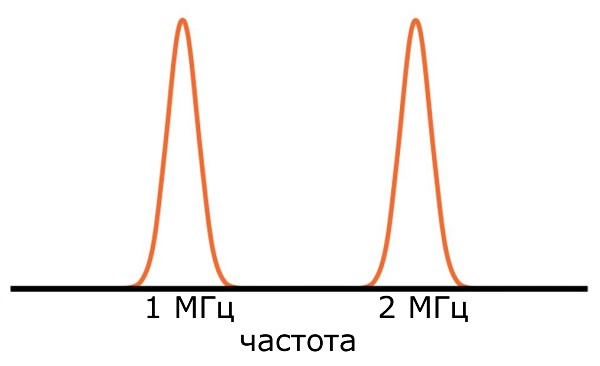
Почему реальный спектр так отличается? Прежде всего, разрешение измерительной системы ограничено, и такие ограничения по своей сути компрометируют любые «идеальные» качества, которые могут присутствовать в исходном сигнале. Но даже если бы у нас было бесконечно точное измерительное устройство, спектр мог бы отличаться от математической версии из-за шума.
Единственным типом сигнала, который мог бы дать «чистые» спектральные компоненты, показанные в предыдущем разделе, является идеальная синусоида (то есть сигнал, в котором отсутствуют шум и изменения в периоде и амплитуде). Любое отклонение от характеристик идеальной синусоиды приведет к появлению дополнительных частотных составляющих.
Интуитивным примером является фазовый шум: нецелесообразно ожидать, что реальный генератор будет всегда выдавать точно выставленную частоту; неизбежно будут присутствовать (надеюсь, малые) изменения в фактической длительности периода, а это называется фазовым шумом. Если вы соберете данные, охватывающие тысячу периодов, а затем выполните спектральный анализ, то фактически усредните частотное содержимое этой тысячи периодов. Результатом будет спектральная форма, показанная выше; ширина сигнала соответствует усредненному отклонению от номинальной частоты.
Спектральные измерения
Диаграммы в частотной области обеспечивают очень удобные значения для обсуждения и анализа радиочастотных систем. Схемы модуляции, помехи, нелинейные искажения – даже базовые спектры, нарисованные на клочке бумаги, могут действительно помочь прояснить ситуацию.
Но, чтобы успешно спроектировать радиочастотную систему, нам, как правило, может понадобиться что-то более сложное. В частности, нам нужно что-то, что даст нам спектральные характеристики реального сигнала. Это важно для охарактеризования работы существующей системы, но обычно более насущной потребностью являются диагностика и анализ: то есть, почему данное устройство не работает, и как мы можем это исправить.
Цифровые осциллографы предлагают функцию «FFT» (БПФ, быстрое преобразование Фурье), это один из способов получения спектральных измерений. Однако инструмент для реального частотного анализа – это анализатор спектра. Это измерительное оборудование, которое специально предназначено для приема высокочастотного входного сигнала и отображения представления этого сигнала в частотной области. Знакомство и небольшой практический опыт работы с анализатором спектра является важным начальным шагом в процессе ознакомления с практическими аспектами радиочастотной инженерии.
Резюме
- Инженеры могут взаимодействовать с электрическими сигналами и через време́нную область, и через частотную область. В контексте радиочастотных сигналов, как правило, более продуктивно и интуитивно понятно работать в частотной области.
- Анализ частотной области естественным образом убирает детали, которые часто маловажны для радиочастотного проектирования и тестирования, и в то же время он подчеркивает те характеристики, на которых нам необходимо сосредоточиться.
- График в частотной области называется спектром. Спектр может удобно показать заметные характерные черты, например, схемы модуляции или реального сигнала, который испытывает проблемы, вызванные помехами.
- Теоретические спектры часто состоят из тонких вертикальных стрелок, которые соответствую идеализированным синусоидам с фиксированной частотой.
- Реальное измерительное оборудование и реальные радиочастотные сигналы всегда имеют дефекты, которые приводят к более широкому изображению сигнала в частотной области.
- Важной частью измерительного оборудования для лаборатории радиочастотного проектирования является анализатор спектра. Эти приборы обеспечивают диаграммы в частотной области, а также различные возможности анализа сигналов.
