Как использовать I/Q сигналы для создания надежного декодера частотной манипуляции (FSK)
Улучшенный алгоритм в сочетании с квадратурной модуляцией может обеспечить декодирование FSK (частотной манипуляции), которое не зависит от фазового рассогласования.
Частоту FSK символа можно идентифицировать, исследуя смещение сигналов по постоянному напряжению, полученных путем умножения принимаемого сигнала на опорные сигналы. Это простой и эффективный способ, который безупречно работает в идеализированной математической среде, но в предыдущей статье мы видели, что он не устойчив к фазовому рассогласованию.
Когда используется некогерентная архитектура приемника, невозможно установить между передатчиком и приемником фиксированную фазовую связь. Это означает, что фаза в начале пакета будет непредсказуемой. Это само по себе не будет нарушать наш алгоритм декодирования, поскольку для идентификации фазы демодулированного сигнала основной полосы частот мы могли бы использовать тренировочную/синхронизирующую последовательность, а затем соответствующим образом модифицировать опорные сигналы. (Однако у меня нет опыта в этом подходе, и я не знаю, насколько он эффективен в реальной жизни.)
Хотя, ситуация становится еще хуже, когда мы рассматриваем кратковременные изменения фазы, так как это может привести к отклонениям фазы принимаемого сигнала от фазы опорного сигнала внутри одного пакета. Таким образом, пакет может быть первоначально согласован по фазе, но ухудшение соотношения фаз приведет к возникновению ошибок в битах, которые вызовут отбрасывание всего пакета.
Прежде чем перейти к остальной часть данной статьи, пожалуйста, уделите минуту, чтобы ознакомиться с нашими ресурсами, которые могут помочь вам лучше ознакомиться с контекстом обсуждения.
Связанная информация
- Цифровая модуляция: амплитуда и частота (из четвертой главы миниучебника о радиочастотном анализе и проектировании)
- Введение в программно определяемые радиосистемы (SDR)
- Понятие дифференциальной квадратурной фазовой манипуляции (DQPSK модуляции)
Предыдущие статьи о цифровой обработке сигналов в Scilab
- Основы цифровой обработки сигналов (ЦОС, DSP) для синусоидальных сигналов с Scilab
- Как выполнить анализ в частотной области с помощью Scilab
- Как использовать Scilab для анализа амплитудно-модулированных РЧ сигналов
- Как использовать Scilab для анализа частотно-модулированных РЧ сигналов
- Как выполнить частотную модуляцию оцифрованным аудиосигналом с помощью Scilab
- Цифровая обработка сигналов в Scilab: как удалить шум в аудиозаписи с помощью фильтров обработки звука
- Обработка звука в Scilab: как реализовать спектральное вычитание
- Цифровая обработка сигналов в Scilab: как декодировать сигнал частотной манипуляции
- Цифровая обработка сигналов в Scilab: понятие фазового рассогласования при декодировании частотной манипуляции (FSK)
Включение квадратурной демодуляции
На решение этой проблемы я указал в конце предыдущей статьи. Мы можем использовать квадратурную демодуляцию для получения I и Q сигналов основной полосы частот, которые позволяют алгоритму декодирования частотной манипуляции (FSK) быть нечувствительным к фазовому рассогласованию.
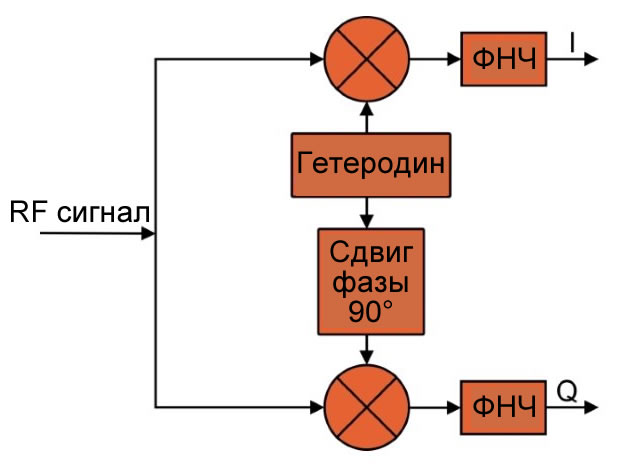
Это очень выгодная модификация системы, но это означает, что нам нужны дополнительные компоненты в схеме демодуляции (для генерации I/Q сигналов вместо одного сигнала основной полосы) и дополнительные тактовые циклы в цифровом сигнальном процессоре (поскольку должны выполняться вычисления с двумя сигналами вместо одного).
Первая проблема довольно незначительна: квадратурная демодуляция в наши дни чрезвычайно распространена, и я думаю, что в большинстве случаев ее можно было бы применять без существенного увеличения стоимости, сложности или размера печатной платы. Серьезность второй проблемы зависит от характеристик вашей системы. Если у вас мощный процессор и низкая скорость передачи данных, у вас не будет никаких проблем, когда вы включите дополнительные математические операции. Но если вы выбрали недорогой маломощный процессор и пытаетесь максимизировать скорость передачи данных, все новые вычисления могут сделать невозможным завершение обработки одного пакета алгоритмом декодирования до того, как поступит следующий пакет.
I/Q декодирование частотной манипуляции в Scilab
Начнем с установления частоты двоичного 0, частоты двоичной 1 и количества выборок на символ, а затем создадим переменную индекса (n) на основе количества выборок на символ
ZeroFrequency = 10e3;
OneFrequency = 30e3;
SamplingFrequency = 300e3;
Samples_per_Symbol = SamplingFrequency/ZeroFrequency;
n = 0:(Samples_per_Symbol-1);
Генерирование I/Q сигналов
Теперь мы можем генерировать символы I и Q для двух частот. По соглашению I (синфазный) сигнал является косинусоидальным сигналом, а Q (сигнал) – синусоидальным сигналом.
Symbol_Zero_I = cos(2*%pi*n / (SamplingFrequency/ZeroFrequency));
Symbol_One_I = cos(2*%pi*n / (SamplingFrequency/OneFrequency));
Symbol_Zero_Q = sin(2*%pi*n / (SamplingFrequency/ZeroFrequency));
Symbol_One_Q = sin(2*%pi*n / (SamplingFrequency/OneFrequency));
subplot(2,2,1)
plot(n, Symbol_Zero_I)
subplot(2,2,2)
plot(n, Symbol_One_I)
subplot(2,2,3)
plot(n, Symbol_Zero_Q)
subplot(2,2,4)
plot(n, Symbol_One_Q)
f = gcf();
for k=1:4
> f.children(k).font_size = 3;
> f.children(k).children.children.thickness = 3;
> end
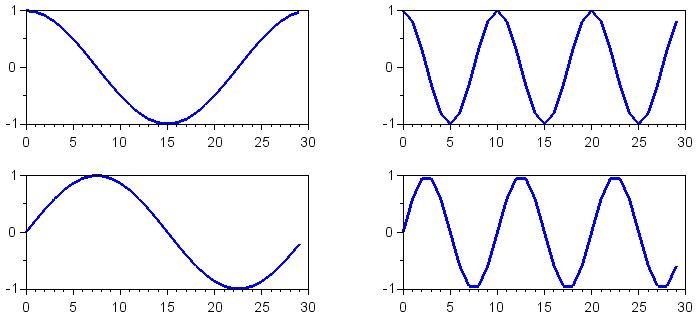
(Цикл for в конце изменяет размер меток для каждого графика и толщину каждой линии. Вы можете сделать то же самое через графический интерфейс, встроенный в окно изображения; использование графического интерфейса более интуитивно, но через некоторое время становится утомительным.)
Наша цель здесь – изучить I/Q решение для фазового рассогласования, поэтому нам понадобятся сдвинутые по фазе версии символов. Как показано в предыдущей статье, наихудшая разность фаз между принятым сигналом и опорным сигналом составляет 90°, поэтому мы будем генерировать символы с фазой 45° (т.е. на полпути между идеальным и наихудшим согласованием) и 90°.
Symbol_Zero_I_45deg = cos(%pi/4 + 2*%pi*n / (SamplingFrequency/ZeroFrequency));
Symbol_One_I_45deg = cos(%pi/4 + 2*%pi*n / (SamplingFrequency/OneFrequency));
Symbol_Zero_Q_45deg = sin(%pi/4 + 2*%pi*n / (SamplingFrequency/ZeroFrequency));
Symbol_One_Q_45deg = sin(%pi/4 + 2*%pi*n / (SamplingFrequency/OneFrequency));
Symbol_Zero_I_90deg = cos(%pi/2 + 2*%pi*n / (SamplingFrequency/ZeroFrequency));
Symbol_One_I_90deg = cos(%pi/2 + 2*%pi*n / (SamplingFrequency/OneFrequency));
Symbol_Zero_Q_90deg = sin(%pi/2 + 2*%pi*n / (SamplingFrequency/ZeroFrequency));
Symbol_One_Q_90deg = sin(%pi/2 + 2*%pi*n / (SamplingFrequency/OneFrequency));
Теперь давайте создадим три набора сигналов основной полосы I и Q для двоичной последовательности 0101.
Baseband_I_aligned = [Symbol_Zero_I Symbol_One_I Symbol_Zero_I Symbol_One_I];
Baseband_Q_aligned = [Symbol_Zero_Q Symbol_One_Q Symbol_Zero_Q Symbol_One_Q];
Baseband_I_45deg = [Symbol_Zero_I_45deg Symbol_One_I_45deg Symbol_Zero_I_45deg Symbol_One_I_45deg];
Baseband_Q_45deg = [Symbol_Zero_Q_45deg Symbol_One_Q_45deg Symbol_Zero_Q_45deg Symbol_One_Q_45deg];
Baseband_I_90deg = [Symbol_Zero_I_90deg Symbol_One_I_90deg Symbol_Zero_I_90deg Symbol_One_I_90deg];
Baseband_Q_90deg = [Symbol_Zero_Q_90deg Symbol_One_Q_90deg Symbol_Zero_Q_90deg Symbol_One_Q_90deg];
subplot(3,2,1)
plot(Baseband_I_aligned)
subplot(3,2,2)
plot(Baseband_Q_aligned)
subplot(3,2,3)
plot(Baseband_I_45deg)
subplot(3,2,4)
plot(Baseband_Q_45deg)
subplot(3,2,5)
plot(Baseband_I_90deg)
subplot(3,2,6)
plot(Baseband_Q_90deg)
f = gcf();
for k=1:6
> f.children(k).font_size = 3;
> end
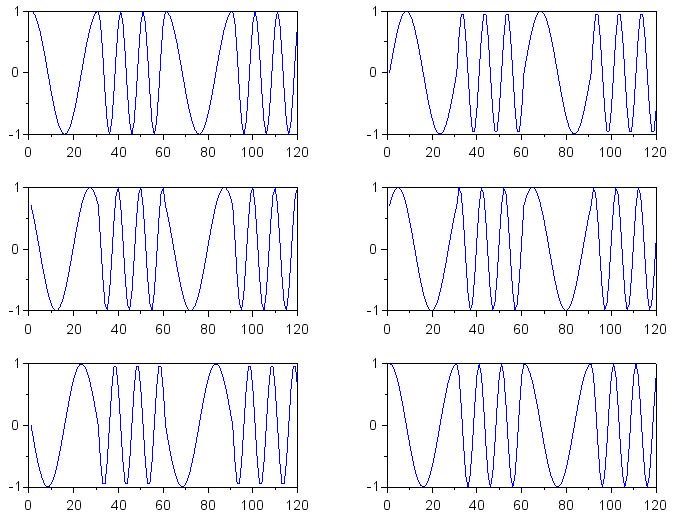
I/Q умножение
Теперь мы можем умножить наши согласованные по фазе и сдвинутые по фазе I/Q сигналы основной полосы на опорные символы. Старайтесь не отвлекаться на длинный список вычислений; всё, что мы делаем, это умножение сигналов I и Q сначала на массив равной длины символов двоичного 0, а затем на массив равной длины символа двоичной 1. Мы должны сделать это три раза, потому что хотим сравнить результаты для версии с согласованной фазой, для версии с фазой 45° и для версии с фазой 90°. Это не отражает реализацию, которая будет выполняться цифровым сигнальным процессором: в реальном приложении будет только один I/Q сигнал основной полосы.
Обратите внимание, что здесь я использую символы I в качестве опорных символов, но я также могу использовать и символы Q. И на самом деле, я мог бы использовать опорный символ с любым значением фазы: путем включения I/Q методов в этот алгоритм декодирования мы сделали процедуру нечувствительной к любому типу расхождения фаз между принятым символом и опорным символом.
DecodeZero_I_aligned = Baseband_I_aligned .* [Symbol_Zero_I Symbol_Zero_I Symbol_Zero_I Symbol_Zero_I];
DecodeZero_Q_aligned = Baseband_Q_aligned .* [Symbol_Zero_I Symbol_Zero_I Symbol_Zero_I Symbol_Zero_I];
DecodeOne_I_aligned = Baseband_I_aligned .* [Symbol_One_I Symbol_One_I Symbol_One_I Symbol_One_I];
DecodeOne_Q_aligned = Baseband_Q_aligned .* [Symbol_One_I Symbol_One_I Symbol_One_I Symbol_One_I];
DecodeZero_I_45deg = Baseband_I_45deg .* [Symbol_Zero_I Symbol_Zero_I Symbol_Zero_I Symbol_Zero_I];
DecodeZero_Q_45deg = Baseband_Q_45deg .* [Symbol_Zero_I Symbol_Zero_I Symbol_Zero_I Symbol_Zero_I];
DecodeOne_I_45deg = Baseband_I_45deg .* [Symbol_One_I Symbol_One_I Symbol_One_I Symbol_One_I];
DecodeOne_Q_45deg = Baseband_Q_45deg .* [Symbol_One_I Symbol_One_I Symbol_One_I Symbol_One_I];
DecodeZero_I_90deg = Baseband_I_90deg .* [Symbol_Zero_I Symbol_Zero_I Symbol_Zero_I Symbol_Zero_I];
DecodeZero_Q_90deg = Baseband_Q_90deg .* [Symbol_Zero_I Symbol_Zero_I Symbol_Zero_I Symbol_Zero_I];
DecodeOne_I_90deg = Baseband_I_90deg .* [Symbol_One_I Symbol_One_I Symbol_One_I Symbol_One_I];
DecodeOne_Q_90deg = Baseband_Q_90deg .* [Symbol_One_I Symbol_One_I Symbol_One_I Symbol_One_I];
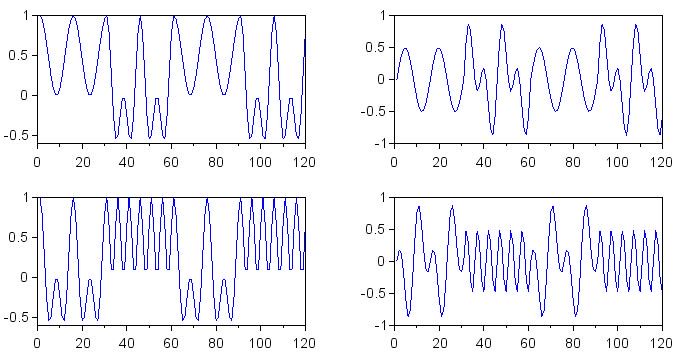
На следующих графиках показаны сигналы, полученные с помощью умножения.
subplot(2,2,1)
plot(DecodeZero_I_aligned)
subplot(2,2,2)
plot(DecodeZero_Q_aligned)
subplot(2,2,3)
plot(DecodeOne_I_aligned)
subplot(2,2,4)
plot(DecodeOne_Q_aligned)
subplot(2,2,1)
plot(DecodeZero_I_45deg)
subplot(2,2,2)
plot(DecodeZero_Q_45deg)
subplot(2,2,3)
plot(DecodeOne_I_45deg)
subplot(2,2,4)
plot(DecodeOne_Q_45deg)
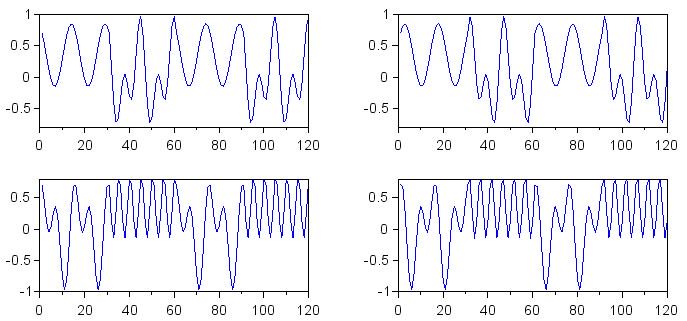
subplot(2,2,1)
plot(DecodeZero_I_90deg)
subplot(2,2,2)
plot(DecodeZero_Q_90deg)
subplot(2,2,3)
plot(DecodeOne_I_90deg)
subplot(2,2,4)
plot(DecodeOne_Q_90deg)

Заключение
Если вы обдумаете последний набор графиков, я думаю, что вы начнете понимать преимущества I/Q обработки в контексте декодирования частотной манипуляции (FSK). По мере того, как фаза входного сигнала теряет согласование с фазой опорного символа, смещение по постоянному напряжению в сигнале, полученном умножением, становится ненадежным показателем сходства между принятой и опорной частотами. Однако наличие сигнала основной полосы, сдвинутого по фазе на 90°, компенсирует этот эффект, поскольку, пока разность фаз для одного сигнала основной полосы приближается к ±90° (наихудший сценарий), фаза другого сигнала основной полосы приближается к 0° или 180° (наилучший результат).
В следующей статье мы продолжим это обсуждение, изучив некоторые дополнительные сведения о том, как интерпретировать и обрабатывать результаты I/Q умножения.
