Основы цифровой обработки сигналов (ЦОС, DSP) для синусоидальных сигналов с Scilab
В данной статье обсуждаются основные задачи обработки сигналов, которые могут быть выполнены с использованием альтернативы для MATLAB с открытым исходным кодом – Scilab.
Что такое цифровая обработка сигналов?
Во-первых, цифровая обработка сигналов (ЦОС, DSP, digital signal processing) – это обработка принятых цифровых сигналов, таких как звук, речь, видео, давление, температура, спектральная плотность или положение и математическое манипулирование ими. Цифровая обработка сигналов является дочерней областью обработки сигналов; аналоговая обработка сигналов также является ее дочерней областью. В данной статье мы обсудим обработку синусоидальных сигналов.
Что такое синусоидальный сигнал?
Синусоидальный сигнал, также известный как синусоида, представляет собой математическую кривую для плавного периодического колебания. Волны синусоиды имеют повторяющуюся картину. Длина повторения называется длиной волны. Синусоиды часто встречаются в математике, физике, технике и, ради этой статьи, в обработке сигналов, а также нескольких других областях.
Scilab против MATLAB
Я много работал с MATLAB на протяжении многих лет, и это, без сомнения, мощный инструмент, который может упростить и ускорить самые разнообразные инженерные задачи. Однако разработка программного обеспечения такого качества точно не дешева, и я не удивлюсь, узнав, что стоимость стандартной лицензии MATLAB не соответствует бюджетным ограничениям многочисленных предпринимателей, консультантов, стартапов и небольших инженерных фирм. Однако оказывается, что есть альтернатива MATLAB, которая полностью бесплатна и называется Scilab.
По моему опыту с Scilab он очень просто и удобен для пользователя. Еще одно преимущество заключается в том, что интерфейс Scilab похож на интерфейс MATLAB, поэтому, если у вас есть опыт работы с MATLAB (возможно, со времен вашего студенчества или работы в большой компании), Scilab должен показаться вам знакомым.
Работа с оцифрованными синусоидами
В мире обработки сигналов синусоиды повсюду. Это так же верно в цифровой сфере, как и в аналоговом мире, и, следовательно, важно до конца понимать природу оцифрованной синусоиды.
Как аналоговые, так и цифровые синусоидальные сигналы имеют амплитуду, частоту и фазу. Для данной статьи нам не нужно беспокоиться о фазе, и амплитуда на самом деле не меняется при переходе от аналога к цифре; частота, с другой стороны, требует некоторого внимания. В аналоговой области частота определяет количество периодов относительно времени. Единицы времени одинаковы всегда и везде – например, 100 Гц (= 100 периодов в секунду) означает в каждом инженерном проекте одно и то же. В цифровой области частота теряет свое отношение к неизменной единице времени. Вместо этого мы имеем отдельные значения амплитуд в соответствии с частотой дискретизации. Это может привести к путанице по двум причинам: 1) используется много разных частот дискретизации, и 2) информация о частоте дискретизации не содержится в последовательности значений амплитуд.
Генерация синусоиды в Scilab
Давайте рассмотрим эту проблему на примере. Мы собираемся использовать Scilab для создания одного периода синусоидального сигнала, который имеет 100 отсчетов за период. Это первая команда:
n = 0:99;
Мы просто создали массив, начинающийся от 0 и заканчивающийся на 99. Вы можете посмотреть в “Variable Browser” (Обозреватель переменных), чтобы подтвердить, что n является одномерным массивом длиной 100.
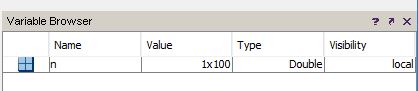
Массив n является цифровым эквивалентом t (т.е. времени) в типовом выражении синусоиды sin(ωt), которое мы используем в аналоговой области. Затем я введу следующие две команды:
y = sin(n);
plot(y)
Это результат:
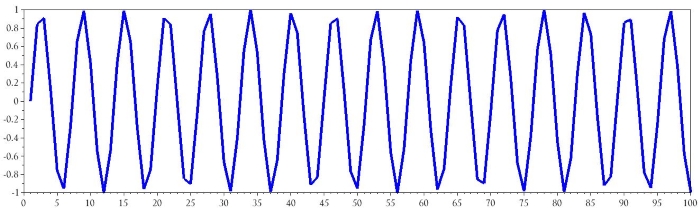
Я знаю, это выглядит ужасно, и это явно неправильно – мы хотели, чтобы один период состоял из 100 отсчетов. Давайте подумаем, почему это произошло:
- синус – это просто функция, которая работает в зависимости от аргумента;
- функция синуса не генерирует уникальные значения для каждого аргумента. Скорее, значения повторяются, когда аргумент изменяется на 2π: sin(0) = sin(2π) = sin(4π) = sin(6π)...
- таким образом, один период значений синуса соответствует диапазону аргумента значений в 2π;
- это означает, что для генерации одного периода значений синусоиды нам нужно изменить массив аргументов так, чтобы он шел от 0 до 2π.
Команда y = sin(n) не создает сигнал нужной формы, потому что аргумент, переданный функции синуса, представляет собой массив, который продолжается от 0 до 99. Решение состоит в том, чтобы разделить n на требуемое количество отсчетов за период, что в данном случае равно 100, а также умножить на 2π:
y = sin(2*%pi*n/100);
Вы можете легко проверить, что это сработает: если n равно нулю, весь аргумент равен нулю; если n равно 100, аргумента равен (2π × 100/100) = 2π; и все числа между ними масштабируются соответствующим образом. Таким образом, мы уменьшили диапазон аргумента до 2π, и всё еще создаем 100 выборок. (Примечание. Я понимаю, что в этом случае n не доходит до 100, но если бы это было так, мы бы хотели, чтобы значение 100 было бы первой выборкой во втором периоде. Другими словами, первый период покрывается 100 значениями от 0 до 99, второй период будет покрываться 100 значениями от 100 до 199, и так далее.) Вот результат:
plot(y)
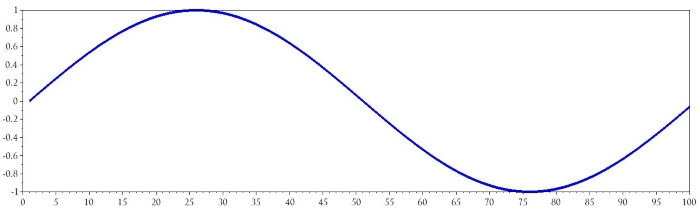
Улучшение графика
С графиком всё еще что-то не так. Мы знаем, что sin(0) = 0, но на графике сигнал имеет значение 0 для значения 1 на горизонтальной оси. Другими словами, сигнал сдвигается на одну выборку вправо. Это происходит потому, что мы не указали список значений горизонтальной оси, которые соответствуют значениям вертикальной оси, содержащимся в массиве y. Если мы скажем Scilab plot(y), он использует для горизонтальной оси значения по умолчанию, и, по-видимому, эти значения по умолчанию начинаются с 1.
Команда y = sin(2*%pi*n/100) генерирует значения y, которые соответствуют номерам в массиве n. Если мы хотим, чтобы график поддерживал эту связь между y и n, мы можем использовать следующую команду:
plot(n, y)
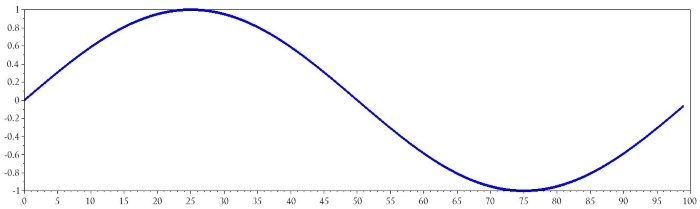
Включение частоты сигнала и частоты дискретизации
Когда мы работаем с реальными синусоидальными сигналами, мы обычно думаем о частоте сигнала (в аналоговой области) и частоте дискретизации (в цифровой области). Таким образом, мы должны интегрировать эти параметры в чисто математические идеи, представляемые до сих пор.
К счастью, это не сложно. Выше мы видели, что аргумент для функции синусоиды должен включать в себя коэффициент (2π / количество выборок за период). Мы можем рассчитать количество отсчетов за период для сигналов реального мира следующим образом:
\[\text{количество выборок за период} = {\text{частота дискретизации} \over \text{частота сигнала}}\]
Предположим, у нас есть система, которая оцифровывает аудиосигнал 6 кГц и отдельный аудиосигнал 2 кГц. Частота дискретизации составляет 44,1 кГц, а АЦП заполняет буфер на 50 выборок. Следующая последовательность команд Scilab может использоваться для генерации значений, которые похожи на данные, созданные реальной системой.
SignalFrequency_1 = 6e3;
SignalFrequency_2 = 2e3;
SamplingFrequency = 44.1e3;
n = 0:49;
Signal_1 = sin(2*%pi*n / (SamplingFrequency/SignalFrequency_1));
Signal_2 = sin(2*%pi*n / (SamplingFrequency/SignalFrequency_2));
plot(n, Signal_1)
plot(n, Signal_2)
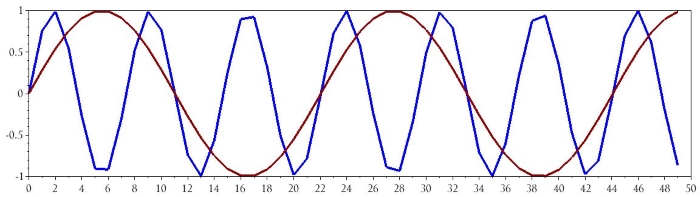
Заключение
В данной статье представлено краткое введение в характеристики оцифрованных синусоид и методы, используемые для создания этих синусоид в Scilab. Я планирую написать дополнительные статьи по обработке и анализу сигналов на основе Scilab; если есть определенная тема, которая, по вашему мнению, будет интересной, не стесняйтесь упоминать ее в комментариях.
