Как обработать I/Q сигналы в программно определяемом радиоприемнике (SDR)
В данной статье рассматривается математическая значимость I/Q сигналов и представлены заключительные этапы DSP алгоритма для декодирования сигналов основной полосы с частотной манипуляцией (FSK).
В этой статье мы обсудим, как завершить разработку алгоритма (начатого в предыдущих статьях), в том числе, как найти смещения по постоянному напряжению для визуализации данных, и как объединить смещения I и Q в одно значение.
Прежде чем продолжить, ознакомьтесь с нашими относящимися к теме ресурсами, которые могут помочь вам лучше ознакомиться с контекстом обсуждения.
Связанная информация
- Цифровая модуляция: амплитуда и частота (из четвертой главы миниучебника о радиочастотном анализе и проектировании)
- Понятие квадратурной демодуляции
Предыдущие статьи о цифровой обработке сигналов в Scilab
- Основы цифровой обработки сигналов (ЦОС, DSP) для синусоидальных сигналов с Scilab
- Как выполнить анализ в частотной области с помощью Scilab
- Как использовать Scilab для анализа амплитудно-модулированных РЧ сигналов
- Как использовать Scilab для анализа частотно-модулированных РЧ сигналов
- Как выполнить частотную модуляцию оцифрованным аудиосигналом с помощью Scilab
- Цифровая обработка сигналов в Scilab: как удалить шум в аудиозаписи с помощью фильтров обработки звука
- Обработка звука в Scilab: как реализовать спектральное вычитание
- Цифровая обработка сигналов в Scilab: как декодировать сигнал частотной манипуляции
- Цифровая обработка сигналов в Scilab: понятие фазового рассогласования при декодировании частотной манипуляции (FSK)
- Как использовать I/Q сигналы для создания надежного декодера частотной манипуляции (FSK)
На чем мы остановились
Последним вычислением, представленным в предыдущей статье о разработке надежного FSK декодера, было умножение трех I/Q сигналов основной полосы (представляющих двоичную последовательность 0101) на опорные символы, используемые для декодирования частотной манипуляции. Результаты были следующими:
Согласованные по фазе сигналы основной полосы
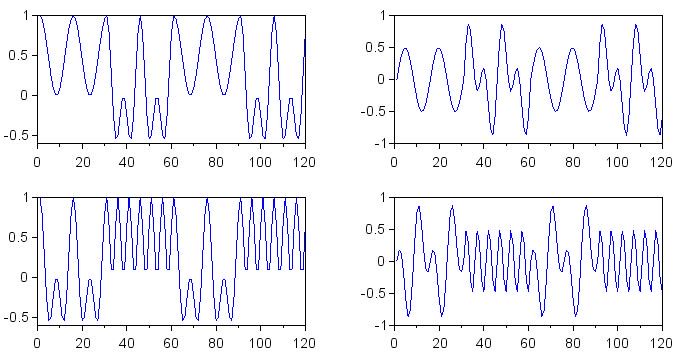
Графики на рисунке 1 представляют результаты для согласованных по фазе сигналов основной полосы. Слева показаны сигналы результатов умножения, полученные из I сигналов основной полосы, а справа показаны сигналы результатов умножения, полученные из Q сигналов основной полосы. Результаты декодирования двоичного нуля находятся в верхней строке, а результаты декодирования двоичной 1 находятся в нижней строке.
Сигналы основной полосы, сдвинутые по фазе на 45°
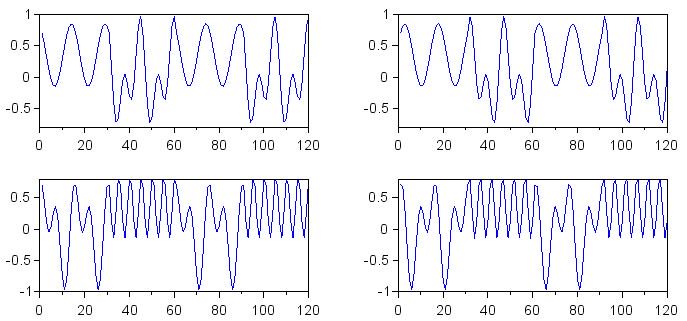
Графики на рисунке 2 представлены для сигналов основной полосы, которые имеют фазовый сдвиг 45°. Как и на рисунке 1, I – слева, Q – справа, декодирование двоичного 0 в верхней строке, а декодирование двоичной 1 в нижней строке.
Сигналы основной полосы, сдвинутые по фазе на 90°

Графики на рисунке 2 представлены для сигналов основной полосы, которые имеют фазовый сдвиг 90°. Организация расположения графиков такая же, как и на двух предыдущих рисунках.
Оценка графиков
Наша цель здесь – сделать систему, которая будет генерировать относительно большое смещение по постоянному напряжению, когда частота принимаемого сигнала очень похожа на частоту опорного сигнала, независимо от соотношения фаз между этими двумя сигналами.
На данный момент давайте посмотрим только на верхний левый график, который показывает декодирование двоичного нуля в принятом I сигнале.
На рисунке 1 имеется большое смещение по постоянному напряжению, соответствующее первому и третьему символам, которые являются символами двоичного 0. На рисунке 2 разность фаз 45° между принятым и опорным сигналами привела к уменьшению смещения по постоянному напряжению символов двоичного 0; однако смещение всё еще довольно велико. На рисунке 3 разность фаз 90° между принятым и опорным сигналами устраняет смещение по постоянному напряжению.
Если вы посмотрите на изменения на верхнем правом графике, то увидите противоположный тренд: смещение символов двоичного 0 начинается с нуля и увеличивается на втором и третьем рисунках. Это эффект «уравновешивания/баланса» обработки I/Q. Генерируя два сигнала основной полосы, которые имеют разность фаз 90°, мы гарантируем, что увеличение фазового рассогласования в одном сигнале основной полосы сбалансировано увеличением фазового согласования в другом сигнале основной полосы.
Графики в нижней строке рисунков демонстрируют такое же поведение, но уже для символов двоичной 1 (то есть для второго и четвертого символов).
I/Q сигналы как комплексные числа
Одним из ключевых моментов к пониманию обработки I/Q сигналов является связь между I/Q компонентами и комплексными числами. Я использую слово «компоненты», потому что I сигналы и Q сигналы, с математической точки зрения, на самом деле сами по себе не сигналы. Они являются синфазной и квадратурной составляющими исходного сигнала и представляют исходный сигнал таким же образом, как действительная и мнимая части комплексного числа представляют собой вектор, состоящий из амплитуды (абсолютного значения) и угла.
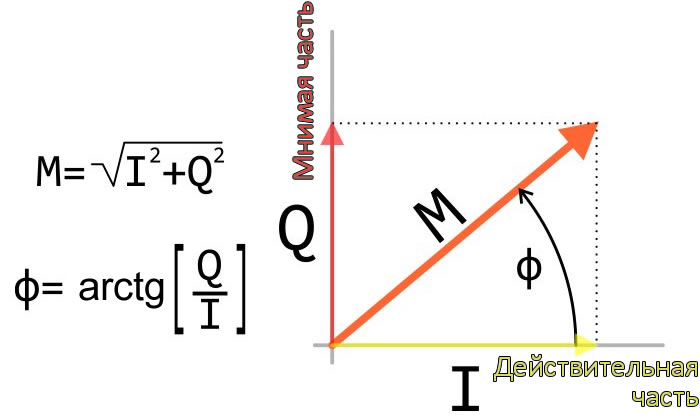
До сих пор мы обрабатывали сигналы I и Q, как если бы они были независимыми, и это приводит к результатам, которые трудно интерпретировать – мы в основном рассматриваем комплексные числа в алгебраической форме, а на самом деле мы хотим знать амплитуду (т.е. модуль, абсолютное значение комплексного числа).
Таким образом, чтобы математически завершить наш алгоритм на основе I/Q сигналов, нам нужно преобразовать компоненты I и Q в амплитуду (модуль комплексного числа).
Как найти смещение по постоянному напряжению
Давайте упростим наши I/Q данные для визуализации, создав графики, соответствующие трем рисунками выше, но с заменой каждого символа на его смещение по постоянному напряжению (что в математическом выражении означает среднее значение). Вы можете вспомнить, что мы сделали в самом конце предыдущей статьи о декодировании сигнала FSK.
for k=1:(length(DecodeZero_I_aligned)/Samples_per_Symbol)
> SymbolOffsets_Zero_I_aligned(((k-1)*Samples_per_Symbol)+1:k*(Samples_per_Symbol)) = mean(DecodeZero_I_aligned (((k-1)*Samples_per_Symbol)+1:k*(Samples_per_Symbol)));
> end
Этот цикл for является шаблоном для всех остальных. Вам понадобится всего 12 циклов, потому что у нас 12 массивов (что соответствует 12 графикам, показанным выше). Единственное, что вам нужно изменить, это массив Decode... и массив SymbolOffsets.... Например:
for k=1:(length(DecodeOne_Q_90deg)/Samples_per_Symbol)
> SymbolOffsets_One_Q_90deg(((k-1)*Samples_per_Symbol)+1:k*(Samples_per_Symbol)) = mean(DecodeOne_Q_90deg (((k-1)*Samples_per_Symbol)+1:k*(Samples_per_Symbol)));
> end
Для построения графиков и улучшения внешнего вида я использовал следующие команды (модифицированные по мере необходимости для других массивов):
subplot(2,2,1)
plot(SymbolOffsets_Zero_I_aligned)
subplot(2,2,2)
plot(SymbolOffsets_Zero_Q_aligned)
subplot(2,2,3)
plot(SymbolOffsets_One_I_aligned)
subplot(2,2,4)
plot(SymbolOffsets_One_Q_aligned)
f = gcf();
for k=1:4
> f.children(k).font_size = 3;
> f.children(k).data_bounds = [0, -0.2; 120, 0.7];
> f.children(k).children.children.thickness = 2;
> end
Ниже приведены результаты. Для каждого набора графиков, результаты расположены следующим образом:
- верхний левый: декодирование нуля, I компонент;
- верхний правый: декодирование нуля, Q компонент;
- нижний левый: декодирование единицы, I компонент;
- нижний правый: декодирование единицы, Q компонент.
Смещения по постоянному напряжению для сигналов основной полосы, согласованных по фазе
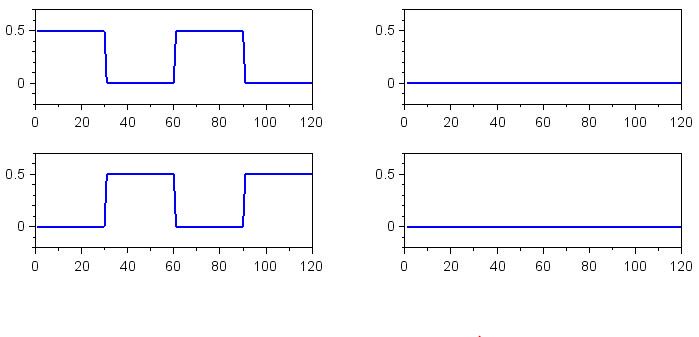
Смещения по постоянному напряжению для сигналов основной полосы, сдвинутых по фазе на 45°
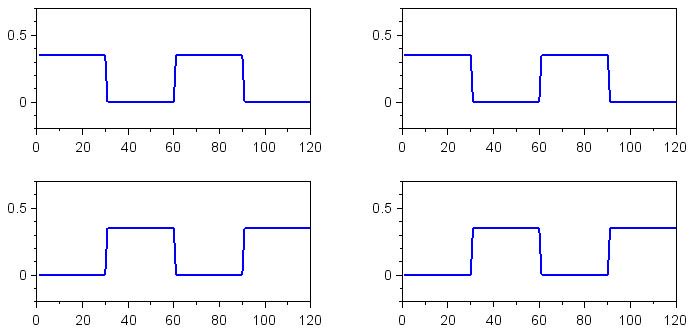
Смещения по постоянному напряжению для сигналов основной полосы, сдвинутых по фазе на 90°
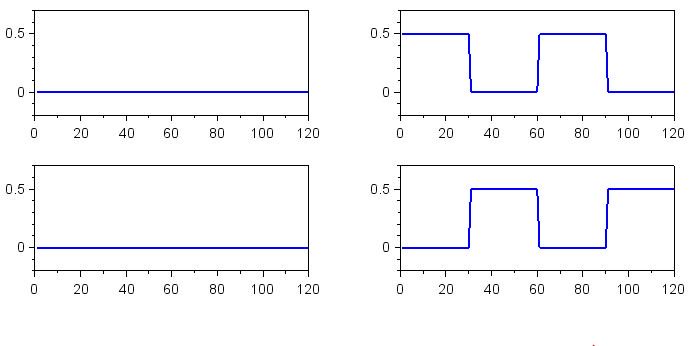
Как конвертировать I/Q в амплитуду (абсолютное значение)
Последним шагом в процессе получения результатов декодирования, независящего от фазы, является объединение смещений I и Q в единое значение декодирования. Это можно сделать следующим образом:
SymbolOffsets_Zero_aligned = sqrt((SymbolOffsets_Zero_I_aligned .* SymbolOffsets_Zero_I_aligned) + (SymbolOffsets_Zero_Q_aligned .* SymbolOffsets_Zero_Q_aligned));
SymbolOffsets_One_aligned = sqrt((SymbolOffsets_One_I_aligned .* SymbolOffsets_One_I_aligned) + (SymbolOffsets_One_Q_aligned .* SymbolOffsets_One_Q_aligned));
SymbolOffsets_Zero_45deg = sqrt((SymbolOffsets_Zero_I_45deg .* SymbolOffsets_Zero_I_45deg) + (SymbolOffsets_Zero_Q_45deg .* SymbolOffsets_Zero_Q_45deg));
SymbolOffsets_One_45deg = sqrt((SymbolOffsets_One_I_45deg .* SymbolOffsets_One_I_45deg) + (SymbolOffsets_One_Q_45deg .* SymbolOffsets_One_Q_45deg));
SymbolOffsets_Zero_90deg = sqrt((SymbolOffsets_Zero_I_90deg .* SymbolOffsets_Zero_I_90deg) + (SymbolOffsets_Zero_Q_90deg .* SymbolOffsets_Zero_Q_90deg));
SymbolOffsets_One_90deg = sqrt((SymbolOffsets_One_I_90deg .* SymbolOffsets_One_I_90deg) + (SymbolOffsets_One_Q_90deg .* SymbolOffsets_One_Q_90deg));
Следующие команды выведут результаты на графики:
subplot(3,2,1)
plot(SymbolOffsets_Zero_aligned)
subplot(3,2,2)
plot(SymbolOffsets_One_aligned)
subplot(3,2,3)
plot(SymbolOffsets_Zero_45deg)
subplot(3,2,4)
plot(SymbolOffsets_One_45deg)
subplot(3,2,5)
plot(SymbolOffsets_Zero_90deg)
subplot(3,2,6)
plot(SymbolOffsets_One_90deg)
f = gcf();
for k=1:6
> f.children(k).font_size = 3;
> f.children(k).data_bounds = [0, -0.2; 120, 0.7];
> f.children(k).children.children.thickness = 2;
> end
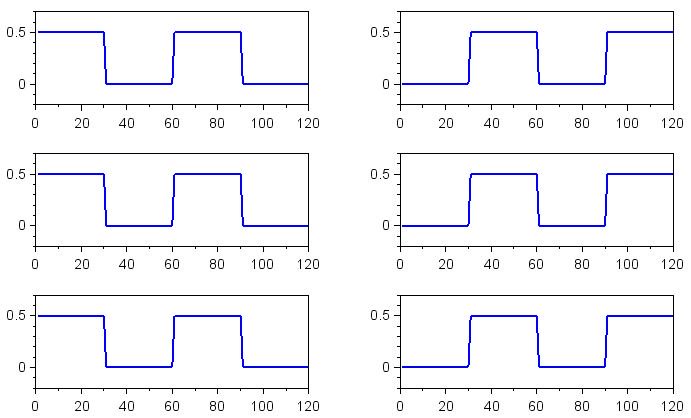
Точное декодирование, независимо от соотношений фаз
Как вы можете видеть, обработка I/Q сигнала устраняет эффект разности фаз между принятым и опорным сигналами. Символы двоичного 0 и двоичной 1 теперь создают полное смещение по постоянному напряжению и могут быть точно декодированы независимо от фазового соотношения между передатчиком и приемником.
Я надеюсь, что теперь вы понимаете значение квадратурной модуляции в декодировании частотной манипуляции (FSK), основанном на цифровой обработке сигналов, и что у вас есть четкие представления о тома, как вы можете реализовать частотную манипуляцию в реальном программно определяемом радиочастотном канале данных.
