Как использовать компьютер для генерации сложных аналоговых сигналов
В данной статье представлен код Scilab, который позволяет генерировать сигналы I/Q, шум и сигналы линейной частотной модуляции на выходе для наушников на компьютере.
В предыдущей статье мы обсуждали, как использовать компьютер в качестве генератора сигналов произвольной формы с помощью технологии, по которой цифровые сигналы создаются в вычислительной программе, такой как Scilab или MATLAB, а затем преобразуются в аналоговые сигналы с помощью звукового оборудования компьютера. Это удобный и простой способ генерирования аналоговых сигналов, которые легко регулируются по частоте и амплитуде.
Однако звуковое оборудование (что вполне разумно) предназначено для звуковых частот, поэтому мы должны смириться с ограниченной полосой частот. Мы, конечно, не собираемся генерировать радиочастотные сигналы напрямую на выходе разъема для наушников.
В предыдущей статье был представлен код Scilab для генерации простой синусоиды и треугольного сигнала. В данной статье я хочу продолжить изучение этой темы, используя сигналы, которые немного интереснее, чем то, что мы рассматривали до сих пор.
Прежде чем двигаться дальше, взгляните на предыдущие статьи по этой теме, чтобы ознакомиться с контекстом обсуждения.
Предыдущие статьи о цифровой обработке сигналов в Scilab
- Основы цифровой обработки сигналов (ЦОС, DSP) для синусоидальных сигналов с Scilab
- Как выполнить анализ в частотной области с помощью Scilab
- Как использовать Scilab для анализа амплитудно-модулированных РЧ сигналов
- Как использовать Scilab для анализа частотно-модулированных РЧ сигналов
- Как выполнить частотную модуляцию оцифрованным аудиосигналом с помощью Scilab
- Цифровая обработка сигналов в Scilab: как удалить шум в аудиозаписи с помощью фильтров обработки звука
- Обработка звука в Scilab: как реализовать спектральное вычитание
- Цифровая обработка сигналов в Scilab: как декодировать сигнал частотной манипуляции
- Цифровая обработка сигналов в Scilab: понятие фазового рассогласования при декодировании частотной манипуляции (FSK)
- Как использовать I/Q сигналы для создания надежного декодера частотной манипуляции (FSK)
- Как обработать I/Q сигналы в программно определяемом радиоприемнике (SDR)
- Как использовать компьютер в качестве генератора сигналов произвольной формы
Генерирование I/Q сигналов
Я немного писал об использовании сигналов I/Q. В двух статьях из серии «Цифровая обработка сигналов в Scilab» представлена подробная информация о преимуществах и деталях реализации сигналов I/Q в контексте конкретного приложения, а на этой странице учебника о радиочастотном проектировании объясняется, как можно получить фазовую модуляцию, изменяя амплитуды I/Q сигналов и затем складывая их вместе. Суть в том, что I/Q технологии являются фундаментальными аспектами обработки сигналов и могут значительно улучшить производительность систем связи.
При этом я очень рад, что в какой-то момент люди настояли на наличии в аудиосистемах двух отдельных каналов (то есть, левого и правого). Не из-за улучшенного впечатления от прослушивания , а потому что левый и правый каналы обеспечивают удобный способ для реализации формирования I/Q сигналов.
До сих пор входным аргументом функции sound() был массив (или, если использовать терминологию Scilab, вектор). Этот массив содержит одну последовательность значений, которая соответствует одному сигналу, и этот один сигнал будет отправлен на оба аудиоканала. Однако входным аргументом также может быть матрица, состоящая из двух массивов, и в этом случае сигнал, соответствующий первому массиву, становится звуком в левом канале, а сигнал, соответствующий второму массиву, становится звуком в правом канале. Следующие команды Scilab дают вам пример генерирования I/Q сигнала с помощью функции sound().
SignalFrequency = 441;
SamplingFrequency = 22.05e3;
Samples_per_Cycle = SamplingFrequency/SignalFrequency;
n = 0:(Samples_per_Cycle-1);
Signal_OneCycle_I = cos(2*%pi*n / (SamplingFrequency/SignalFrequency));
Signal_OneCycle_Q = sin(2*%pi*n / (SamplingFrequency/SignalFrequency));
CycleDuration = (1/SamplingFrequency) * length(n);
FullSignal_I = 0;
FullSignal_Q = 0;
for k=1:(10/CycleDuration)
> FullSignal_I = [FullSignal_I Signal_OneCycle_I];
> FullSignal_Q = [FullSignal_Q Signal_OneCycle_Q];
> end
FullSignal_IQ = [FullSignal_I; FullSignal_Q];
sound(FullSignal_IQ)
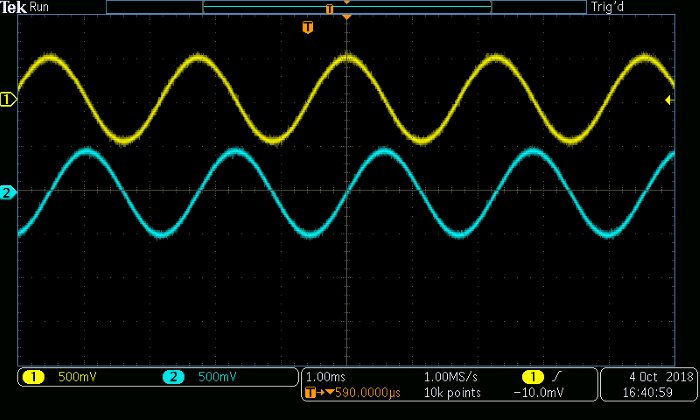
Создание шума
Многие инженеры-электронщики посвящают значительную часть своего времени подавлению шума. Следовательно, в намеренном создании шума есть нечто странное. Однако подача зашумленного сигнала может помочь вам определить, как схема будет реагировать на определенный тип шума.
Допустим, у вас есть схема датчика, которая иногда подвергается высокочастотным помехам от соседнего устройства. Чтобы определить, как этот шум повлияет на выходной сигнал усилителя датчика, вы можете смоделировать шум в Scilab и наложить его на сигнал, который напоминает входной сигнал усилителя. Эта цифровая версия зашумленного входного сигнала может быть затем преобразована в аналоговый сигнал и подана на реальную схему усилителя.
Следующие команды Scilab предоставляют пример генерирования зашумленного сигнала. Входной сигнал представляет собой треугольный сигнал 110,25 Гц, а шум состоит из двух синусоид меньшей амплитуды с частотами 2 кГц и 3,5 кГц.
SignalFrequency = 110.25;
SamplingFrequency = 22.05e3;
Samples_per_Cycle = SamplingFrequency/SignalFrequency;
n = 0:(Samples_per_Cycle-1);
CycleDuration = (1/SamplingFrequency) * length(n);
LowerLimit = -1;
UpperLimit = 1;
StepSize = (UpperLimit - LowerLimit)/(length(n)/2);
UpwardRamp = LowerLimit:StepSize:(UpperLimit - StepSize);
DownwardRamp = UpperLimit:-StepSize:(LowerLimit + StepSize);
TriangleWave_OneCycle = [UpwardRamp DownwardRamp];
TriangleWave_Full = 0;
NoiseFrequency1 = 2e3;
NoiseFrequency2 = 3.5e3;
NoiseComponent1 = 0.1*sin(2*%pi*n / (SamplingFrequency/ NoiseFrequency1));
NoiseComponent2 = 0.1*sin(2*%pi*n / (SamplingFrequency/ NoiseFrequency2));
NoisySignal_OneCycle = TriangleWave_OneCycle + NoiseComponent1 + NoiseComponent2;
NoisySignal_Full = 0;
for k=1:(10/CycleDuration)
> NoisySignal_Full = [NoisySignal_Full NoisySignal_OneCycle];
> end
sound(NoisySignal_Full)

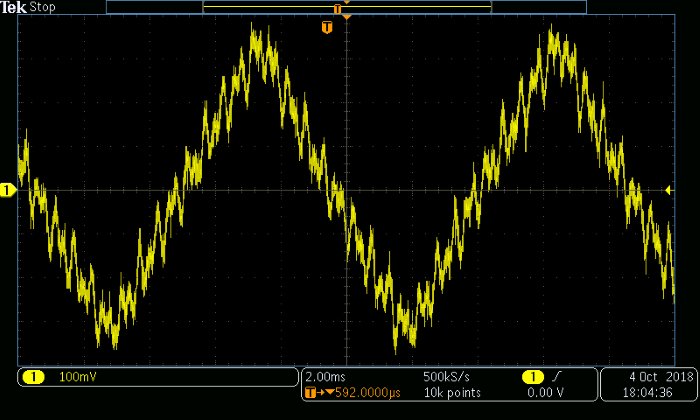
Сигнал линейной частотной модуляции (сигнал качающейся частоты)
Удобным способом определения амплитудно-частотной характеристики (частотного отклика) реальной схемы является обеспечение входного сигнала, который быстро увеличивается (или уменьшается) по частоте. Затем вы можете посмотреть на выходной сигнал на осциллографе и пронаблюдать связь между частотой и амплитудой, и вы можете даже построить график Боде (график амплитудно-частотной характеристики в логарифмическом масштабе), измеряя амплитуду на различных частотах и отмечая результаты на графике.
Сигнал, который демонстрирует этот вид преднамеренного постоянного увеличения или уменьшения частоты называется сигналом линейной частотной модуляции (ЛЧМ) (другими вариантами его названия являются «сигнал качающейся частоты», «сигнал частотной развертки», «sweep signal», «frequency-sweep signal»). Создание легко настраиваемых сигналов качающейся частоты в аналоговой схемотехнике – это не то, что я бы назвал простой задачей, но наша система «Scilab/MATLAB в аналог» делает процесс проектирования быстрым и относительно простым.
Команды Scilab, приведенные ниже, будут генерировать сигнал качающейся частоты, который начинается от 10 Гц и заканчивается примерно на 10 кГц. Способ увеличения частоты заключается в следующем:
- Начальный период составляет 1/(10 Гц) = 0,1 с. Изменения по частоте происходят относительно этого исходного периода.
- Я хочу, чтобы каждая частота выполняла целое число периодов синусоидального сигнала, то есть синусоидальный сигнал должен начинаться на нуле и заканчиваться на нуле. Это гарантирует, что у сигнала качающейся частоты не будет разрывов, которые создают ложные высокочастотные составляющие.
- После каждого отрезка времени, соответствующего начальному периоду, частота увеличивается в два раза. Это позволяет нам быстро охватить частотный диапазон и избежать разрывов, так как каждая частота будет целым кратным минимальной частоты.
MinimumFrequency = 10;
MaximumFrequency = 10e3;
SamplingFrequency = 48e3;
Samples_per_Cycle = SamplingFrequency/MinimumFrequency;
n = 0:(Samples_per_Cycle-1);
Chirp = 0;
InstantaneousFrequency = MinimumFrequency;
Chirp = sin(2*%pi*n / (SamplingFrequency/InstantaneousFrequency));
while (InstantaneousFrequency < MaximumFrequency)
> InstantaneousFrequency = InstantaneousFrequency * 2;
> Waveform_at_NextFrequency = sin(2*%pi*n / (SamplingFrequency/InstantaneousFrequency));
> Chirp = [Chirp Waveform_at_NextFrequency];
> end
Так сигнал качающейся частоты выглядит в Scilab:
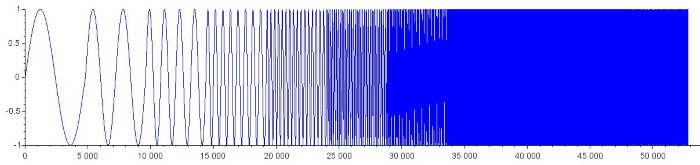
А это две осциллограммы:
sound(Chirp, 48e3)
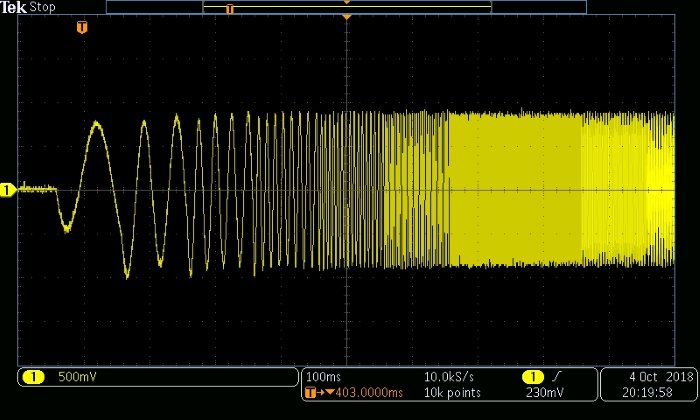
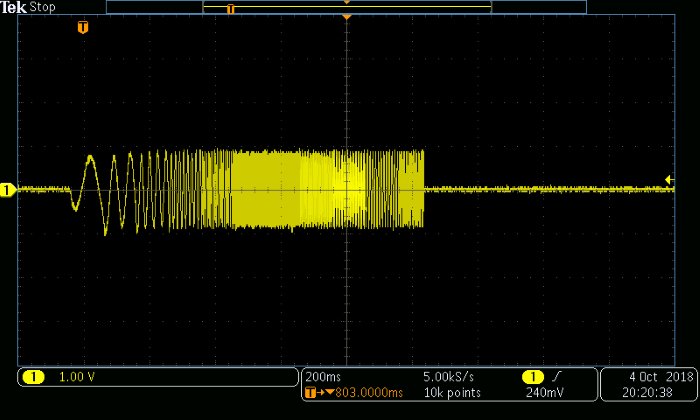
Похоже, что аудиокарта имеет инвертирующий усилитель на выходе ЦАП – обратите внимание, как сигнал качающейся частоты на графике Scilab начинается с положительной полуволны (как и следовало ожидать для нормальной синусоиды), и как на осциллограмме сигнал начинается с отрицательной полуволны.
Какие сигналы вы хотели бы увидеть?
Мы сгенерировали несколько интересных аналоговых сигналов, используя Scilab и обычный выход для наушников на компьютере. Если у вас есть идеи относительно других полезных сигналов, которые могут быть получены этим методом, дайте нам знать в комментариях ниже.
