Как выполнить анализ в частотной области с помощью Scilab
В данной статье мы будем работать с синусоидальными сигналами в частотной области с использованием функционала быстрого преобразования Фурье (FFT) в Scilab.
Вспомогательная информация
В предыдущей статье были представлены введение в Scilab и концепция генерации цифровой синусоиды, а также мы использовали команду plot() для отображения осциллограмм во временной области. Основная цель этой статьи – понять и получить опыт работы с командой fft() Scilab, которая позволяет отображать сигналы в частотной области. Однако представление одночастотного синусоидального сигнала в частотной области не очень интересно, и в следующей статье мы рассмотрим частотный анализ в контексте радиочастотной модуляции.
Быстрое преобразование Фурье (БПФ, FFT)
Преобразование Фурье обеспечивает способ идентификации частотного содержания сигнала. Оригинальное преобразование Фурье представляет собой математическую процедуру, которая принимает выражение, которое является функцией от времени, и выдает выражение, которое является функцией от частоты. Если мы хотим генерировать такой же тип информации в контексте дискретизированных сигналов, мы можем использовать дискретное преобразование Фурье, сокращенно ДПФ или DFT. Я предполагаю, что некоторые люди, которые часто слышали термин «FFT», не знакомы с термином «DFT». БПФ (быстрое преобразование Фурье) – это просто название, используемое для обозначения алгоритмов, которые могут эффективно выполнять вычисления DFT.
Мы можем генерировать данные DFT для сигнала, включив соответствующий массив в качестве аргумента команды fft(). Однако такая команда, такая как fft(BasebandSignal), не будет выводить данные, которые могут отображаться как типовая диаграмма в частотной области.
Первая причина этого заключается в том, что результаты вычисления DFT являются комплексными числами, которые передают информацию об амплитуде и фазе. Часто нас интересует только амплитуда частотных составляющих сигнала, и мы можем извлечь эти данные об амплитуде с помощью команды abs().
Другой проблемой является отсутствие фактических частот, мы обсуждали в предыдущей статье это усложнение, хотя и в отношении сигналов во временной области. Когда у нас есть команда, такая как fft(BasebandSignal), входной массив представляет собой просто последовательность чисел. Эта последовательность чисел ничего не говорит о соответствующих частотах реального мира, и поэтому, чтобы создать более информативный спектр, мы должны предоставить эту информацию в другом месте.
Дискретное преобразование Фурье синусоидальной волны
В этой статье мы будем работать с сигналом основной полосы (немодулированный, низкочастотный сигнал) 10 кГц и несущей 100 кГц (эту несущую я выбрал для удобства, в типовом радиочастотном приложении она будет намного выше). Частота дискретизации будет равна 1 МГц.
Начнем с создания сигнала основной полосы, а затем рассмотрим графики во временной и частотной областях.
BasebandFrequency = 10e3;
SamplingFrequency = 1e6;
BufferLength = 200;
n = 0:(BufferLength - 1);
BasebandSignal = sin(2*%pi*n / (SamplingFrequency/BasebandFrequency));
plot(n, BasebandSignal)
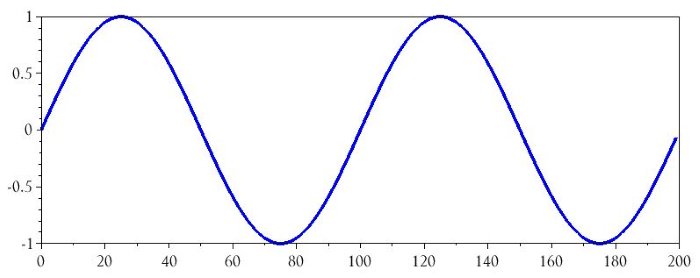
Следующие команды будут генерировать представление этого сигнала в частотной области:
BasebandDFT = fft(BasebandSignal);
BasebandDFT_magnitude = abs(BasebandDFT);
plot(BasebandDFT_magnitude)
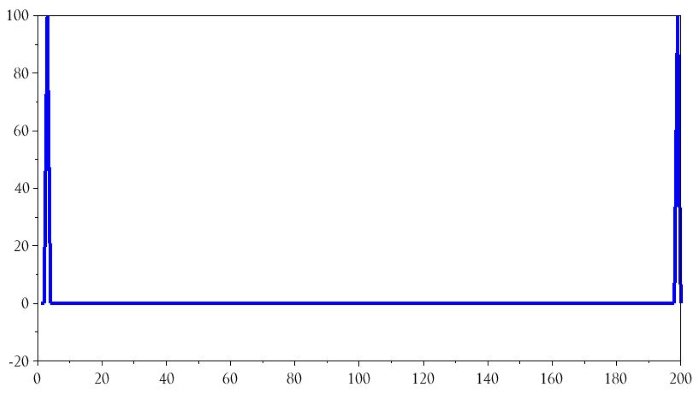
Я бы не стал называть эту диаграмму особенно полезной, но это хорошее начало. Первая проблема заключается в том, что одночастотный синусоидальный сигнал привел к появлению двух частотных составляющих DFT. Это происходит потому, что расчеты DFT генерируют симметричные результаты, т.е. правая половина диаграммы является зеркальным отображением левой половины диаграммы. Мы можем устранить эту путаницу следующим образом:
plot(BasebandDFT_magnitude(1:(BufferLength/2)))
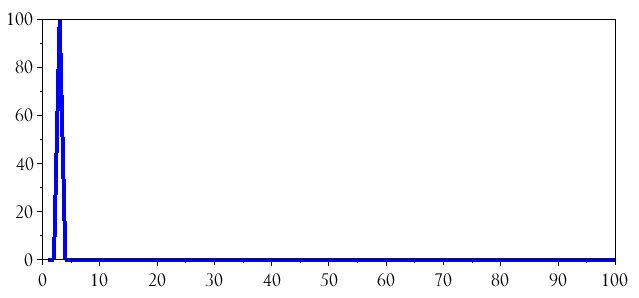
Всё, что мы здесь сделали, – это команда plot() для отображения только первой половины данных. Давайте увеличим всплеск:
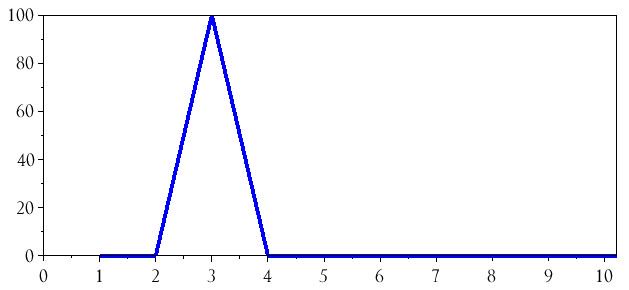
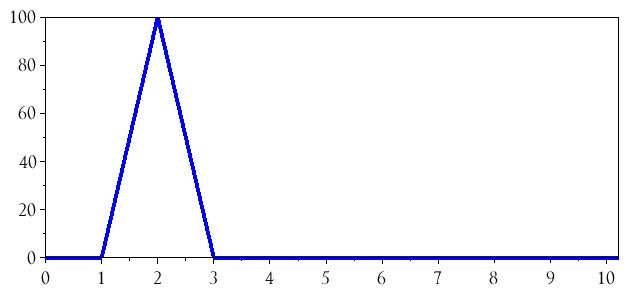
Почему частотная составляющая соответствует отметке 3 на горизонтальной оси? Ну, если вы посмотрите на график во временной области, массив, который был передан команде fft(), имеет два полных периода синусоидальной волны. В среде DFT это становится «частотой» 2, и поскольку наш график начинается на горизонтальной оси со значения 1 вместо 0, «частота» 2 находится по горизонтальной оси на отметке 3. Мы можем исправить эту запутанную ситуацию, построив результаты FFT в соответствии с массивом n:
plot(n(1:(BufferLength/2)), BasebandDFT_magnitude(1:(BufferLength/2)))
Введение реальных частот
Сейчас спектр показывает единственную частотную составляющую на отметке 2; следующий шаг – изменить горизонтальную ось так, чтобы значения на ней соответствовали реальным частотам, используемым в системе. К счастью, это не сложно. Рассмотрим следующие замечания:
- На результат DFT влияет длина буфера. Если бы у нас был буфер с 300 выборками, было бы 3 полных периода низкочастотного сигнала (сигнала основной полосы), и всплеск DFT был бы расположен на отметке 3 на горизонтальной оси, вместо отметки 2. Таким образом, нам нужно в модификацию горизонтальной оси каким-то образом включить длину буфера.
- Частота дискретизации является основным эталоном для всей системы дискретизации. Как только сигналы оцифрованы, их отношение к абсолютному времени заменяется отношением к частоте дискретизации.
- Самая высокая частота, которую может обрабатывать система, равна частоте дискретизации (fд), деленной на 2. В контексте данной системы дискретизации частоты выше fд/2 не существуют, потому что их нельзя отличить от соответствующих нижних частот.
Значения на горизонтальной оси результатов ДПФ подсчитываются с равномерно разнесенными шагами от 0 до максимальной частоты системы, а размер шага определяется длиной буфера. Таким образом, для введения реальных частот в спектр ДПФ нам нужно построить график амплитуд относительно последовательности значений, которые увеличиваются от 0 до fд/2 (фактически, чтобы получить правильную длину массива, диапазон будет идти до значения непосредственно предшествующего значению fд/2). Мы можем сделать это следующим образом:
HalfBufferLength = BufferLength/2;
HorizAxisIncrement = (SamplingFrequency/2)/HalfBufferLength;
DFTHorizAxis = 0:HorizAxisIncrement:((SamplingFrequency/2)-HorizAxisIncrement);
plot(DFTHorizAxis, BasebandDFT_magnitude(1:HalfBufferLength))
xlabel("Frequency (Hz)")
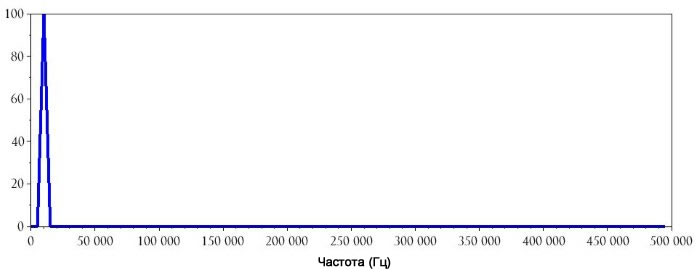
То же самое, но с увеличенным масштабом по оси частот:
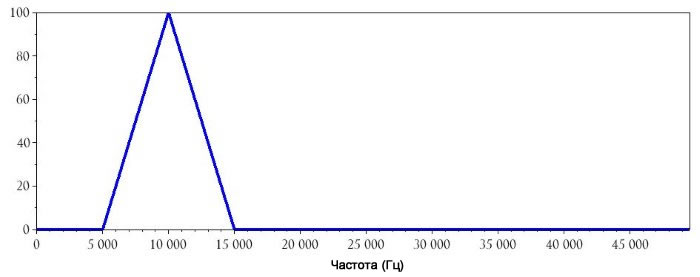
Как вы можете видеть, частотный компонент низкочастотного сигнала теперь идентифицируется как 10 кГц. Мы можем следовать той же процедуре и для сигнала несущей 100 кГц:
CarrierSignal = sin(2*%pi*n / (SamplingFrequency/CarrierFrequency));
CarrierDFT = fft(CarrierSignal);
CarrierDFT_magnitude = abs(CarrierDFT);
plot(DFTHorizAxis, CarrierDFT_magnitude(1:HalfBufferLength))
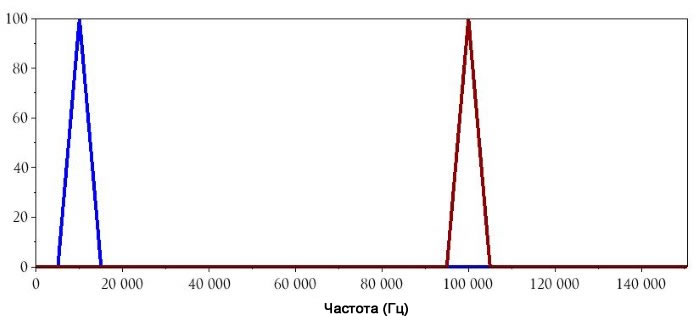
Заключение
Я надеюсь, что эта статья помогла вам разобраться, как интерпретировать данные, предоставляемые дискретным преобразованием Фурье. Теперь вы можете использовать Scilab для анализа частотных составляющих сигналов, которые вы создали математически или захватили с помощью аналого-цифрового преобразования.
