Как использовать Scilab для анализа амплитудно-модулированных РЧ сигналов
FFT функционал Scilab может помочь вам понять влияние методов радиочастотной модуляции в частотной области.
Вспомогательная информация
- Учимся жить в частотной области (из первой главы миниучебника)
- Множество типов радиочастотной модуляции (и другие страницы из главы 4 миниучебника)
В предыдущей статье мы ввели команду fft() Scilab и обсудили, как мы можем манипулировать результатами FFT, чтобы они передавали четкую информацию об амплитуде частотных компонентов в дискретизированном сигнале. Однако анализ БПФ, выполненный в предыдущей статье, был не особенно полезен – он просто показал нам, что синусоида имела один спектральный компонент с частотой, которую мы специально выбрали в начале процесса. Данная статья должна быть более интересной: мы будем использовать дискретный по времени анализ Фурье, чтобы получить представление об эффектах амплитудной модуляции.
Модуляция в частотной области
Модуляция создает изменения, которые очевидны на диаграмме модулированного сигнала во временной области. Зачем же нам нужно создавать диаграмму в частотной области?
Ну, для полного ответа на этот вопрос я рекомендую посмотреть статью по первой ссылке в разделе вспомогательной информации. Короткий ответ таков: спектр модулированного сигнала дает нам интуитивное, четкое представление о важной информации, которую трудно или в некоторых случаях невозможно извлечь из графика во временной области. Спектральный анализ также может помочь нам понять, что происходит при модуляции; графики во временной области включают в себя детали, которые не нужны, когда необходимо обдумать основные взаимодействия между частотами низкочастотного модулирующего сигнала и частотой сигнала несущей.
Создание графиков в частотной области для модулированных сигналов
Во-первых, давайте создадим окружение Scilab с переменными, которые нам понадобятся во всей оставшейся части статьи.
BasebandFrequency = 10e3;
CarrierFrequency = 100e3;
SamplingFrequency = 1e6;
BufferLength = 200;
n = 0:(BufferLength - 1);
BasebandSignal = sin(2*%pi*n / (SamplingFrequency/BasebandFrequency));
CarrierSignal = sin(2*%pi*n / (SamplingFrequency/CarrierFrequency));
plot(n, BasebandSignal)
plot(n, CarrierSignal)
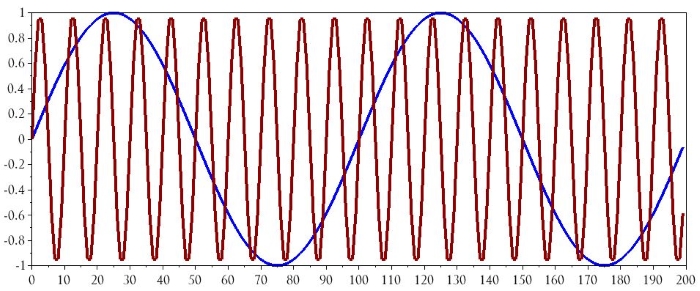
Амплитудная модуляция одночастотным сигналом
Основным математическим соотношением для амплитудной модуляции является следующее:
\(x_{АМ}(t)=\sin(\omega_нt)(1+x_{нч}(t))\)
Несущая представлена с помощью sin(ωнt), поэтому мы здесь выполним смещение низкочастотного сигнала (сигнала основной полосы) вверх (так, чтобы его значения всегда были положительными), а затем умножим несущую на сдвинутый немодулированный сигнал. Вот соответствующая команда Scilab:
ModulatedSignal_AM = CarrierSignal .* (1+BasebandSignal);
Одной очень важной деталью является точка перед звездочкой. В среде CarrierSignal и BasebandSignal являются матрицами, и если вы используете только звездочку между матрицами, Scilab предполагает, что вы хотите выполнить матричное умножение. В этой ситуации мы не хотим выполнять матричное умножение (и на самом деле это даже невозможно, потому что количество столбцов в первой матрице не равно количеству строк во второй матрице).
Мы пытаемся воспроизвести типовое аналоговое умножение, где мгновенное значение одного сигнала многократно умножается на соответствующее мгновенное значение другого сигнала. Это означает, что нам нужно использовать «поэлементное» умножение, где первый элемент CarrierSignal умножается на первый элемент BasebandSignal, второй элемент CarrierSignal умножается на второй элемент BasebandSignal, и так далее. Мы достигаем этого, используя оператор .* вместо оператора *.
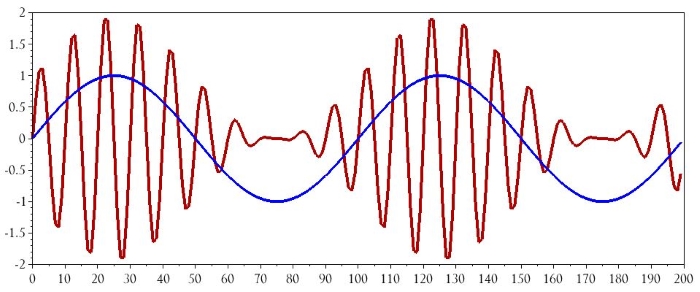
Ниже приведены результаты во временной области:
plot(n, BasebandSignal)
plot(n, ModulatedSignal_AM)
Теперь давайте создадим горизонтальную ось нашего DFT преобразования:
HalfBufferLength = BufferLength/2;
HorizAxisIncrement = (SamplingFrequency/2)/HalfBufferLength;
DFTHorizAxis = 0:HorizAxisIncrement:((SamplingFrequency/2)-HorizAxisIncrement);
Следующие команды создадут график в частотной области:
AM_DFT = fft(ModulatedSignal_AM);
AM_DFT_magnitude = abs(AM_DFT);
plot(DFTHorizAxis, AM_DFT_magnitude(1:HalfBufferLength))
xlabel("Frequency (Hz)")
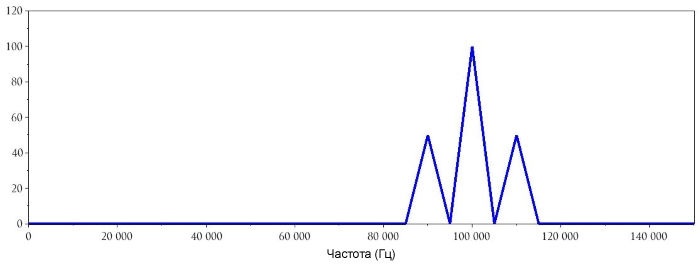
У нас есть спектр, состоящий из доминирующего всплеска на несущей частоте и двух боковых полос, соответствующих несущей частоте плюс частота НЧ сигнала и несущей частоте минус частота НЧ сигнала. Умножение двух сигналов сдвинуло спектр низкочастотного сигнала основной полосы (который имеет всплески на положительных 10 кГц и отрицательных 10 кГц), так что он центрируется относительно несущей частоты.
Амплитудная модуляция с несколькими частотами в модулирующем сигнале
Обычно модулирующий сигнал не является одночастотной синусоидой: модуляция – это способ передачи информации с помощью высокочастотной несущей, а в неизменном синусоидальном сигнале 10 кГц информации не так много. Если мы передаем, скажем, голосовую запись или изменяющиеся показания температуры, частота низкочастотного сигнала основной полосы будет варьироваться в определенном диапазоне.
Чтобы создать более реалистичный спектр АМ сигнала, мы можем создать сигнал основной полосы с несколькими частотами, а затем следовать той же процедуре ДПФ, которая была использована выше:
BufferLength = 1000;
n = 0:(BufferLength - 1);
Baseband_1 = sin(2*%pi*n / (SamplingFrequency/BasebandFrequency));
Baseband_2 = sin(2*%pi*n / (SamplingFrequency/(BasebandFrequency/2)));
Baseband_3 = sin(2*%pi*n / (SamplingFrequency/(BasebandFrequency/4)));
Baseband_4 = sin(2*%pi*n / (SamplingFrequency/(BasebandFrequency/8)));
Baseband_5 = sin(2*%pi*n / (SamplingFrequency/(BasebandFrequency/10)));
BasebandSignal = [Baseband_1 Baseband_2 Baseband_3 Baseband_4 Baseband_5];
BufferLength = BufferLength * 5;
n = 0:(BufferLength - 1);
Здесь я создаю пять синусоид с разными частотами в диапазоне от 1 кГц до 10 кГц (я увеличил длину буфера до 1000, чтобы каждая синусоида имела, по крайней мере, один полный период). Затем я объединил эти синусоиды в один длинный низкочастотный сигнал основной полосы (и соответственно я увеличил длину буфера). Именно так теперь выглядит сигнал во временной области:
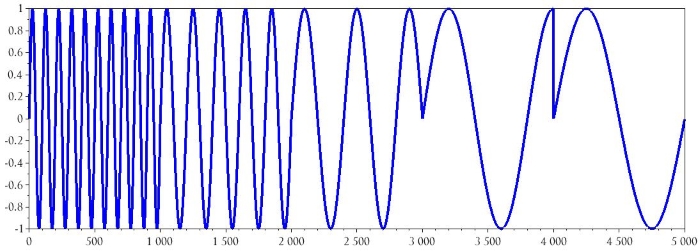
Частота сигнала несущей не изменена, но нам всё равно нужно создать новый сигнал, поскольку длина массива CarrierSignal должна быть такой же, как длина массива BasebandSignal.
CarrierSignal = sin(2*%pi*n / (SamplingFrequency/CarrierFrequency));
Теперь мы генерируем новый амплитудно-модулированный сигнал, создаем новую последовательность значений на горизонтальной оси DFT, проводим вычисления FFT и выводим данные на график.
ModulatedSignal_AM = CarrierSignal .* (1+BasebandSignal);
HalfBufferLength = BufferLength/2;
HorizAxisIncrement = (SamplingFrequency/2)/HalfBufferLength;
DFTHorizAxis = 0:HorizAxisIncrement:((SamplingFrequency/2)-HorizAxisIncrement);
AM_DFT = fft(ModulatedSignal_AM);
AM_DFT_magnitude = abs(AM_DFT);
plot(DFTHorizAxis, AM_DFT_magnitude(1:HalfBufferLength))
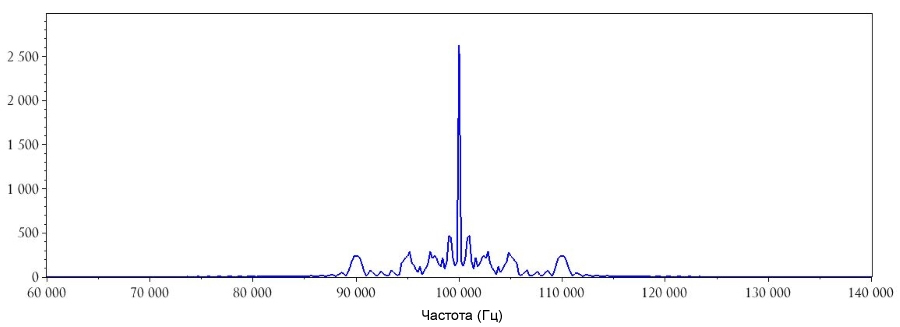
Заключение
В данной статье мы использовали Scilab для исследования эффектов амплитудной модуляции в частотной области при модуляции одночастотным сигналом, также мы сгенерировали сигнал основной полосы с изменяющейся частотой, чтобы можно было увидеть пример более реалистичного спектра АМ сигнала. В следующей статье я планирую рассмотреть характеристики спектра частотно-модулированного сигнала.
