Цифровая обработка сигналов в Scilab: понятие фазового рассогласования при декодировании частотной манипуляции (FSK)
В данной статье мы будем использовать Scilab для изучения влияния непредсказуемых изменений фазы в демодулированном сигнале основной полосы с частотной манипуляцией (FSK).
Вспомогательная информация
- Цифровая модуляция: амплитуда и частота (из четвертой главы миниучебника о радиочастотном анализе и проектировании)
- Как демодулировать цифровую фазовую модуляцию
Предыдущие статьи о цифровой обработке сигналов в Scilab
- Основы цифровой обработки сигналов (ЦОС, DSP) для синусоидальных сигналов с Scilab
- Как выполнить анализ в частотной области с помощью Scilab
- Как использовать Scilab для анализа амплитудно-модулированных РЧ сигналов
- Как использовать Scilab для анализа частотно-модулированных РЧ сигналов
- Как выполнить частотную модуляцию оцифрованным аудиосигналом с помощью Scilab
- Цифровая обработка сигналов в Scilab: как удалить шум в аудиозаписи с помощью фильтров обработки звука
- Обработка звука в Scilab: как реализовать спектральное вычитание
- Цифровая обработка сигналов в Scilab: как декодировать сигнал частотной манипуляции
В предыдущей статье о том, как декодировать сигнал частотной манипуляции (FSK), мы видели, что для идентификации частоты в заданном фрагменте принятого сигнала может быть использовано умножение. Если мы знаем, что символ имеет одну из двух частот, мы умножаем принятый сигнал на опорные сигналы, соответствующие этим двум частотам, и сигнал, возникающий в результате этого умножения, будет иметь относительно большое смещение по постоянному напряжению, если частота принятого сигнала аналогична частоте опорного сигнала. Эта процедура основана на следующем тригонометрическом тождестве:
\[\sin(\omega_1t) \cdot \sin(\omega_2t)=\frac{1}{2}(\cos((\omega_1-\omega_2)t)-\cos((\omega_1+\omega_2)t))\]
или
\[\cos(\omega_1t) \cdot \cos(\omega_2t)=\frac{1}{2}(\cos((\omega_1-\omega_2)t)+\cos((\omega_1+\omega_2)t))\]
Однако здесь есть важная деталь: эти тождества включают в себя две синусоидальные волны или две косинусоидальные волны. Другими словами, правая часть уравнения действительна только тогда, когда два перемножаемых сигнала согласованы по фазе. Что произойдет, если фазы не согласованы? Например, что, если перемножаемые сигналы имеют разность фаз 90°? Поскольку синус и косинус не совпадают по фазе на 90°, мы можем ответить на этот вопрос, рассмотрев другое тригонометрическое тождество:
\[\sin(\omega_1t) \cdot \cos(\omega_2t)=\frac{1}{2}(\sin((\omega_1+\omega_2)t)+\sin((\omega_1-\omega_2)t))\]
Теперь ситуация совершенно иная. Правая часть уравнения имеет два синусоидальных члена, вместо двух косинусоидальных членов, и, следовательно, связь между входными частотами и смещением по постоянному напряжению теряется. Если мы вводим два сигнала с одинаковыми частотами и разностью фаз 90°, то вместо cos(0) мы имеем sin(0), а sin(0) = 0.
Генерирование и визуализация разностей фаз
Мы можем использовать тренировочную/синхронизирующую последовательность, которая предшествует действительному пакету, чтобы идентифицировать точку, в которой заканчивается один символ, и начинается следующий символ. Теоретически это должно позволить нам установить синхронизацию передатчика-приемника, которая продолжает работать во время всей остальной части пакета. Однако этот подход не является особенно надежным, поскольку фазовый сдвиг в принимаемом сигнале может происходить довольно быстро.
Фазовому сдвигу способствует многолучевое распространение, а условия, влияющие на многолучевое распространение, могут быстро изменяться, когда приемник, передатчик или соседние объекты находятся в движении. Относительное движение между передатчиком и приемником также способствует непредсказуемым изменениям фазы. Возможно, вы сможете установить согласование фаз в начале пакета, но это не означает, что вы по-прежнему будете иметь согласованные фазы в конце или даже в середине пакета.
Выше мы видели, что фазовый сдвиг на 90° разрушает этот алгоритм декодирования. Это наихудший сценарий; эффективность алгоритма декодирования неуклонно уменьшается, когда разность фаз между принятым сигналом основной полосы и опорным сигналом приближается к 90°.
Давайте рассмотрим некоторые команды Scilab, которые помогут нам визуализировать эффект фазового рассогласования. Во-первых, мы создадим несколько переменных и два опорных сигнала.
ZeroFrequency = 10e3;
OneFrequency = 30e3;
SamplingFrequency = 300e3;
Samples_per_Symbol = SamplingFrequency/ZeroFrequency;
n = 0:(Samples_per_Symbol-1);
Symbol_Zero = sin(2*%pi*n / (SamplingFrequency/ZeroFrequency));
Symbol_One = sin(2*%pi*n / (SamplingFrequency/OneFrequency));
Теперь мы собираемся создать матрицу, состоящую из восьми принятых сигналов основной полосы с фазой, которая увеличивается от 0° до 180° с шагом 22,5°.
for k = 0:8
> Phase = k*(%pi/8);
> RxSymbol = sin(Phase + (2*%pi*n / (SamplingFrequency/ZeroFrequency)));
> RxSignal(k+1, 1:length(n)*4) = [RxSymbol RxSymbol RxSymbol RxSymbol];
> end
Чтобы добраться до этого момента, мы сначала создаем массив RxSymbol, который состоит из одного периода, затем мы объединяем четыре из этих символов, чтобы создать сигнал основной полосы. Переменная RxSignal – это многомерный массив, он содержит 9 массивов, причем каждый из этих массивов представляет собой последовательность значений, соответствующих четырем периодам сигнала основной полосы с частотой 10 кГц (т.е. с частотой двоичного 0) и фазой 0, 22,5°, 45°, 67,5°, 90°, 112,5°, 135°, 157,5° или 180°.
Использование многомерного массива позволяет легко генерировать двумерный или трехмерный график всех сигналов. 2D график может быть сгенерирован следующим образом:
for k = 0:8
> plot(RxSignal(k+1,:))
> end
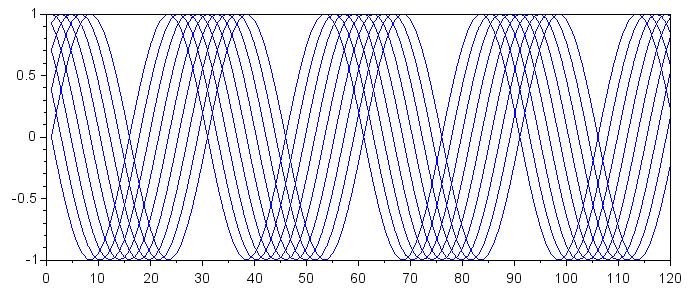
Я предпочитаю 3D изображение:
mesh(RxSignal)
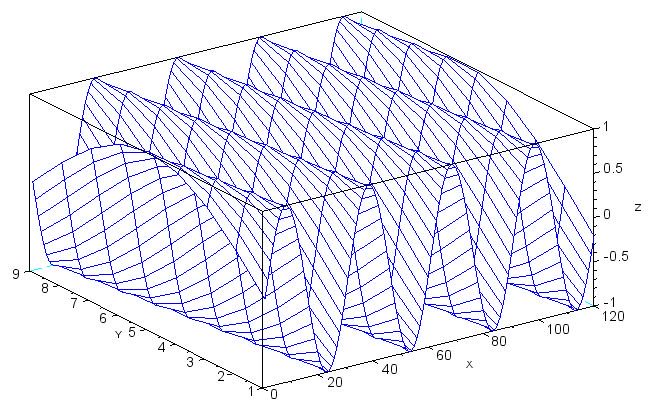
Если у вас возникли проблемы с интерпретацией этого графика, обратите внимание, что сигнал при значении 1 на оси y начинается со значения 0 на оси z и продолжается к более высоким значениям на оси z. Это синусоидальная волна с фазовым членом, равным 0. Начальная точка сигналов постепенно изменяется при переходе к более высоким значениям по оси y. В конце концов, вы достигнете значения 9 по оси y, где сигнал начинается с 0, но переходит к более низким значениям оси z, это синусоидальная волна с фазовым сдвигом 180°.
Влияние фазового рассогласования
Теперь мы можем умножить все эти сигналы основной полосы на опорный сигнал двоичного 0, а затем вычислить среднее значение, чтобы увидеть, как смещение по постоянному напряжению зависит от фазы. Помните, что все эти сигналы имеют одинаковую частоту; меняется только фаза.
for k = 0:8
> Offsets_Zero(k+1, 1:length(n)*4) = mean(RxSignal(k+1, :) .* [Symbol_Zero Symbol_Zero Symbol_Zero Symbol_Zero]);
> end
mesh(Offsets_Zero)
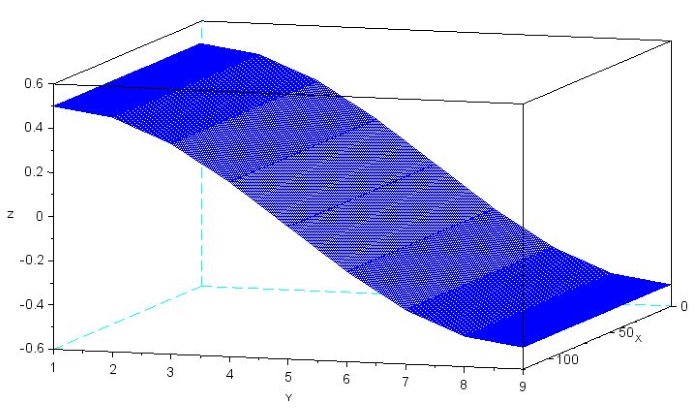
Следующий график более уместен для нашего обсуждения, потому что нам важна величина смещения, а не его знак.
mesh(abs(Offsets_Zero))
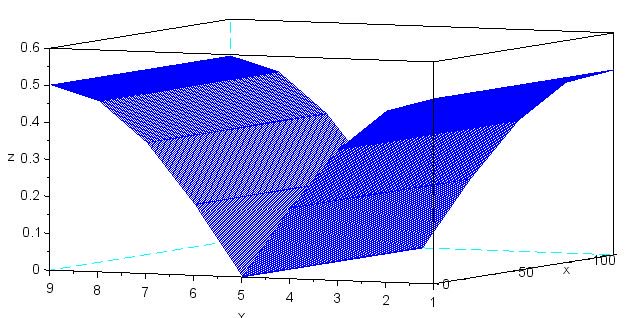
Как вы можете видеть, величина смещения по постоянному напряжению постепенно уменьшается по мере того, как разность фаз приближается к 90°. Таким образом, если разность фаз между принятым сигналом и опорным сигналом близка к 90°, смещение по постоянному напряжению будет указывать на отсутствие существенного сходства между частотой символа и частотой двоичного нуля, даже если частота символа точно такая же, как частота двоичного 0.
Решение
Проблема фазового рассогласования может быть предопределена путем включения квадратурной демодуляции в архитектуру приемника.
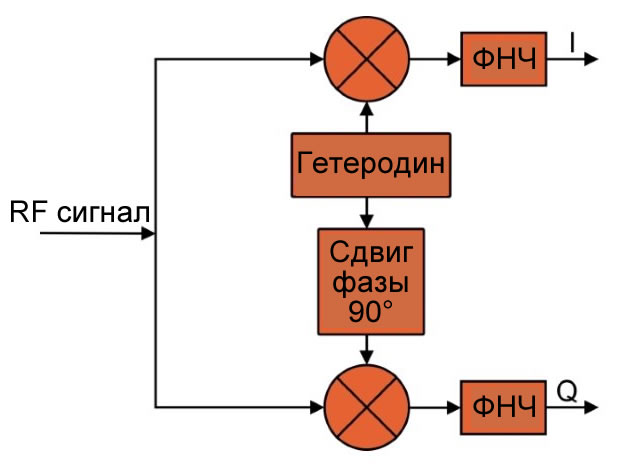
Квадратурная демодуляция создает два сигнала основной полосы, которые имеют относительный сдвиг фаз 90°. Эти сигналы называются I (синфазный) и Q (квадратурный), и они являются именно тем, что нам нужно, если мы хотим предотвратить математический сбой, который происходит, когда разность фаз между принятым символом и опорным сигналом приближается к 90°.
В следующей статье мы рассмотрим использование сигналов I/Q для улучшенного декодирования частотной манипуляции (FSK).
