Частотная модуляция: теория, временная и частотная области

Хотя менее и интуитивно понятная, чем амплитудная модуляция, частотная модуляция (ЧМ, англ. FM) по-прежнему является довольно простым способом беспроводной передачи данных.

Мы все, по крайней мере, смутно знакомы с частотной модуляцией – это источник термина «FM радио». Если мы считаем частоту тем, что имеет мгновенное значение, а не как нечто, состоящее из нескольких периодов сигнала, деленных на соответствующий период времени, мы можем непрерывно изменять частоту в соответствии с мгновенной величиной низкочастотного сигнала.

Математика

В первой статье данной главы мы обсудили парадоксальную величину, называемую мгновенной частотой. Если вы считаете этот термин незнакомым или запутанным, вернитесь на эту страницу и прочитайте раздел «Частотная модуляция (ЧМ, англ. FM) и фазовая модуляция (ФМ, англ. PM)». Тем не менее, вы всё еще можете быть немного запутаны, и это понятно: идея мгновенной частоты нарушает основной принцип, согласно которому «частота» указывает, как часто сигнал завершает полный цикл: десять раз в секунду, миллион раз в секунду или сколько бы то ни было раз.

Мы не будем пытаться заниматься каким-либо тщательным или всесторонним рассмотрением мгновенной частоты в качестве математической концепции. (Если вы намерены подробно изучить эту проблему, вот академический документ, который должен помочь.) В контексте FM важно понять, что мгновенная частота естественно вытекает из того, что частота сигнала несущей изменяется непрерывно в ответ на модулирующую волну (т.е. низкочастотный сигнал). Мгновенное значение модулирующего сигнала влияет на частоту в определенный момент, а не на частоту одного или нескольких полных циклов.

На самом деле это верно только для аналоговой частотной модуляции; в цифровой ЧМ один бит соответствует дискретному числу циклов. Это приводит к интересной ситуации, когда более старая технология (аналоговая ЧМ) менее интуитивно понятна, чем более новая технология (цифровая частотная модуляция, также называемая частотной манипуляцией или FSK (Frequency Shift Keying)).

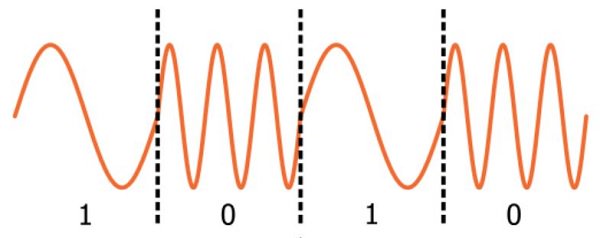
Как и в предыдущей статье мы будем обозначать несущую как sin(ω_несt). У нее уже есть частота (а именно, ω_нес), поэтому мы должны использовать термин «дополнительное отклонение частоты» для обозначения частотной составляющей, внесенной процедурой модуляции. Этот термин несколько вводит в заблуждение, поскольку «дополнительное» подразумевает более высокую частоту, тогда как модуляция может приводить к несущей частоте, которая выше или ниже номинальной несущей частоты. Фактически поэтому частотная модуляция (в отличие от амплитудной модуляции) не требует смещенного низкочастотного сигнала: положительные значения низкочастотного сигнала увеличивают частоту несущей, а отрицательные значения низкочастотного сигнала уменьшают частоту несущей. В этих условиях демодуляция не является проблемой, поскольку все значения низкочастотного сигнала соответствуют уникальным частотам.

В любом случае, вернемся к нашему сигналу несущей: sin(ω_несt). Если мы добавим низкочастотный сигнал (x_нч) к величине внутри круглых скобок, мы получим отклонение фазы, линейно пропорциональное низкочастотному сигналу. Но нам нужна частотная модуляция, а не фазовая, поэтому мы хотим, чтобы линейно пропорционально низкочастотному сигналу было отклонение частоты. Из первой статьи данной главы мы знаем, что мы можем получить частоту, взяв производную фазы по времени. Таким образом, если мы хотим, чтобы частота была пропорциональна x_нч, мы должны добавить не сам низкочастотный сигнал, а скорее интеграл от низкочастотного сигнала (поскольку взятие производной отменяет интеграл, у нас остается x_нч как отклонение частоты).

\[x_{чм}(t)=\sin\left(\omega_{нес}t+\int_{-\infty}^{t} x_{нч}(t)dt\right)\]

Единственное, что нам нужно здесь добавить, это индекс модуляции m. В предыдущей статье мы увидели, что индекс модуляции можно использовать для того, чтобы изменения амплитуды несущей были более или менее чувствительны к изменениям амплитуды низкочастотного сигнала. Его функция в FM аналогична: индекс модуляции позволяет нам точно настраивать интенсивность изменения частоты, которое возникает при изменении амплитуды низкочастотного сигнала.

\[x_{чм}(t)=\sin\left(\omega_{нес}t+m \int_{-\infty}^{t} x_{нч}(t)dt\right)\]

Временна́я область

Давайте посмотрим на несколько сигналов во временной области. Ниже показана наша несущая 10 МГц:

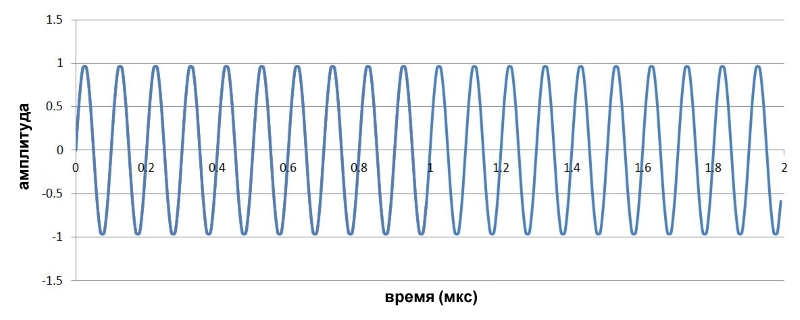
Низкочастотным модулирующим сигналом будет синусоида 1 МГц, показанная ниже:

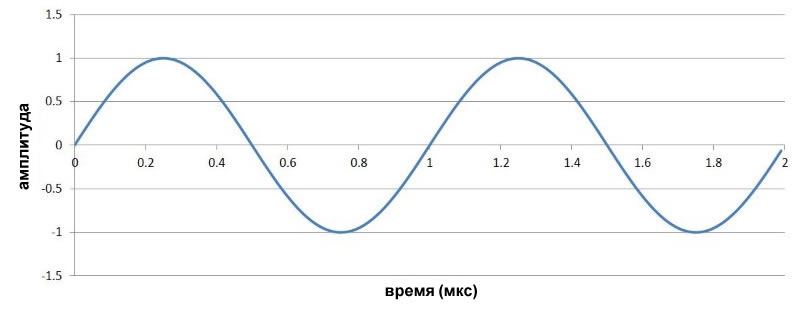
Частотно-модулированный сигнал генерируется с помощью формулы, приведенной выше. Интеграл от sin(x) равен -cos(x) + C. Константа C здесь не важна, поэтому для вычисления FM сигнала мы можем использовать следующую формулу:

\[x_{чм}(t)=\sin((10\times10^6\times2\pi t)-\cos(1\times10^6\times2\pi t))\]

Результат показан ниже (красным показан низкочастотный модулирующий сигнал):

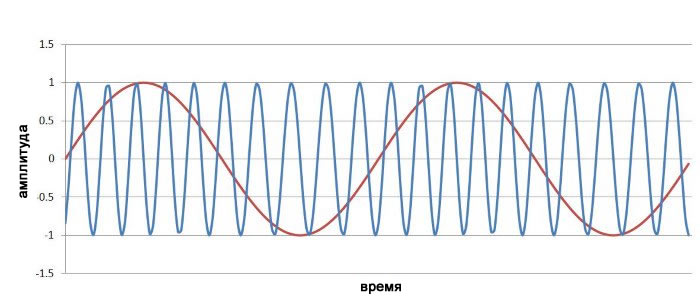
Похоже, что несущая не изменилась, но если присмотреться, пики немного ближе друг к другу, когда низкочастотный модулирующий сигнала приближается к своему максимальному значению. Итак, у нас есть частотная модуляция; но проблема заключается в том, что изменения модулирующего сигнала не создают достаточного изменения частоты несущей. Мы можем легко исправить эту ситуацию, увеличив индекс модуляции. Используем m=4.

\[x_{чм}(t)=\sin((10\times10^6\times2\pi t)-4\cos(1\times10^6\times2\pi t))\]

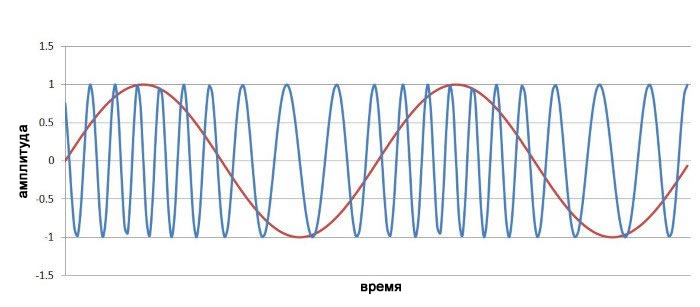
Теперь мы можем более четко видеть, как частота модулированной несущей непрерывно следует за мгновенным значением амплитуды низкочастотного модулирующего сигнала.

Частотная область

Формы AM и FM сигналов при одинаковых сигнале несущей и низкочастотном модулирующем сигнале выглядят совершенно по-разному. Поэтому интересно обнаружить, что AM и узкополосная FM дают аналогичные изменения в частотной области. (Узкополосная частотная модуляция предусматривает ограниченную полосу модулирующего сигнала и позволяет упростить анализ.) В обоих случая низкочастотный спектр (включая отрицательные частоты) переносится в полосу, которая простирается выше и ниже несущей частоты. В AM спектр самого низкочастотного модулирующего сигнала сдвигается вверх. В FM это спектр интеграла низкочастотного модулирующего сигнала, который появляется в полосе, окружающей несущую частоту.

Для модуляции, показанной выше, с m=1 мы получаем следующий спектр:

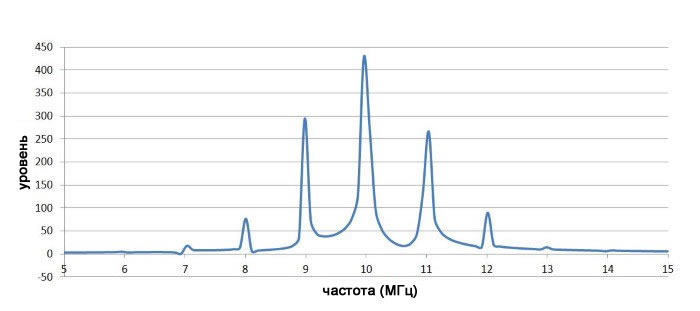
Следующий спектр соответствует m=4:

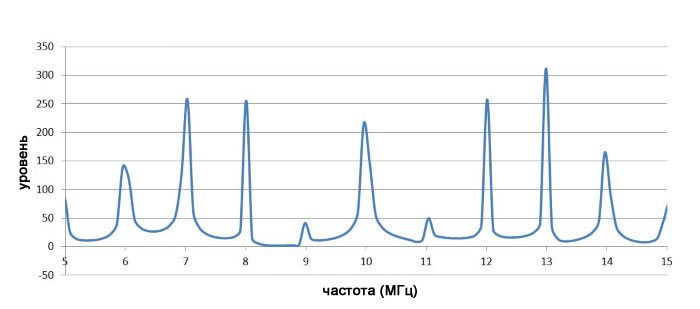
Это очень ясно показывает, что индекс модуляции влияет на частотные составляющие частотно-модулированного сигнала. Спектральный анализ частотной модуляции сложнее, чем для амплитудной модуляции; поэтому для частотно-модулированных сигналов трудно предсказать ширину полосы частот.

Резюме

• Математическое представление частотной модуляции состоит из синусоидального выражения с интегралом низкочастотного модулирующего сигнала, добавленного к аргументу функции синуса или косинуса.
• Индекс модуляции может использоваться, чтобы сделать отклонение частоты более чувствительным или менее чувствительным к изменениям амплитуды низкочастотного модулирующего сигнала.
• Узкополосная частотная модуляция приводит к переносу спектра интеграла низкочастотного модулирующего сигнала в полосу, окружающую несущую частоту.
• На спектр ЧМ влияет индекс модуляции, а также отношение амплитуды модулирующего сигнала к частоте модулирующего сигнала.

Теги