Понятие квадратурной демодуляции
В данной статье объясняется, что такое квадратурная демодуляция, и дается представление о характере I/Q сигналов.
Если вы прочитали предыдущую статью, вы знаете, что такое I/Q сигналы, и как выполняется квадратурная (то есть на основе I/Q сигналов) модуляция. В этой статье мы обсудим квадратурную демодуляцию, которая является универсальным методом извлечения информации из амплитудно-, частотно- и фазо-модулированных сигналов.
Преобразование в I и Q
На следующей диаграмме представлена базовая структурная схема квадратурного демодулятора.
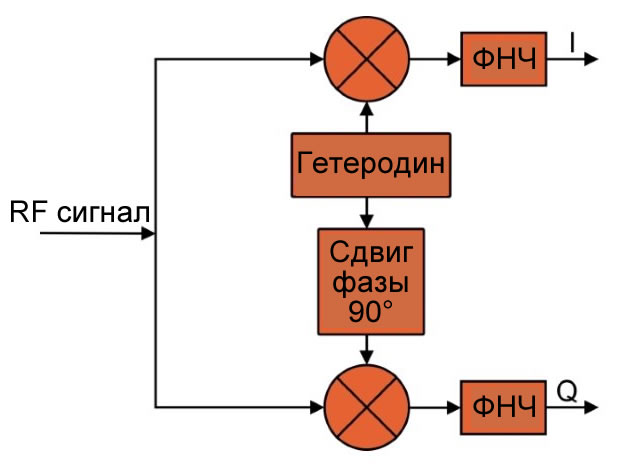
Вы легко заметите, что эта схема похожа на квадратурный модулятор в обратном порядке. Радиочастотный сигнал умножается на сигнал гетеродина (для канала I) и на сигнал гетеродина, сдвинутый на 90° (для канала Q). Результат (после фильтрации нижних частот, который будет вкратце объяснен позже) представляет собой сигналы I и Q, которые готовы для дальнейшей обработки.
В квадратурной модуляции мы используем низкочастотные I/Q сигналы для создания амплитудно-, частотно- или фазо-модулированного сигнала, который будет усилен и передан. В квадратурной демодуляции мы преобразуем имеющийся модулированный сигнал в соответствующие низкочастотные I/Q сигналы. Важно понимать, что принятый сигнал может быть от передатчика любого типа – квадратурная демодуляция не ограничивается сигналами, которые изначально были созданы посредством квадратурной модуляции.
Фильтры нижних частот необходимы, потому что квадратурное умножение, применяемое к принятому сигналу, ничем не отличается от умножения, используемого, например, в обычном амплитудном демодуляторе. Спектр принятого сигнала будет сдвинут вниз и вверх на значение частоты несущей (fнес); таким образом, фильтр нижних частот необходим для подавления высокочастотных составляющих, связанных со спектром, центрированным вокруг 2fнес.
Если вы прочитали статью про амплитудную демодуляцию, предыдущий абзац мог дать вам понять, что квадратурный демодулятор фактически состоит из двух амплитудных демодуляторов. Разумеется, вы не можете применять обычную амплитудную демодуляцию к частотно-модулированному сигналу; в амплитуде FM сигнала нет закодированной информации. Но квадратурная (амплитудная) демодуляция может захватить информацию, закодированную в частоте, – это просто (довольно интересный) характер I/Q сигналов. Используя два амплитудных демодулятора, приводимых в действие синусоидами с частотой сигнала несущей и с разностью фаз в 90°, мы генерируем два разных низкочастотных сигнала, которые вместе могут сообщать информацию, закодированную посредством изменений частоты или фазы принимаемого сигнала.
Квадратурная амплитудная демодуляция
Как упоминалось в первой статье этой главы, «Как демодулировать амплитудно-модулированный сигнал», один из подходов амплитудной демодуляции включает в себя умножение принимаемого сигнала на опорный сигнал с частотой несущей, а затем НЧ фильтрацию результатов этого умножения. Этот метод обеспечивает более высокую производительность, чем амплитудная демодуляция на базе пикового детектора с утечкой. Однако этот подход имеет серьезную слабость: на результат умножения влияет соотношение фаз сигнала несущей передатчика и опорного сигнала несущей частоты в приемнике.
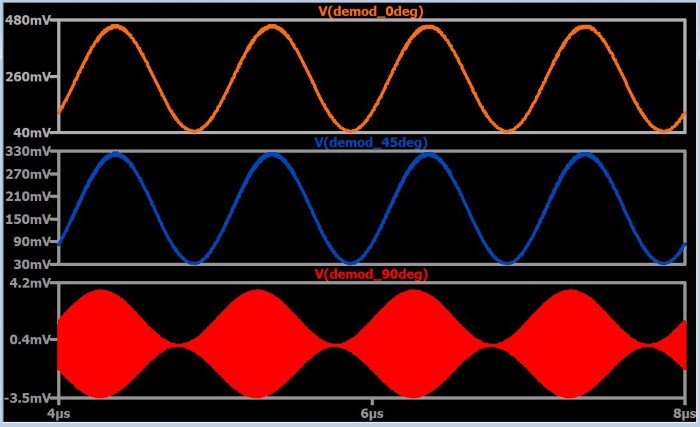
Эти диаграммы показывают демодулированный сигнал для трех значений разности фаз передатчика и приемника. По мере увеличения разности фаз амплитуда демодулированного сигнала уменьшается. Процедура демодуляции стала нерабочей при разности фаз 90°, это представляет собой наихудший сценарий, т.е. амплитуда начинает увеличиваться снова, когда разность фаз удаляется (в любом направлении) от 90°.
Один из способов исправить эту ситуацию заключается в использовании дополнительной схемы, которая синхронизирует фазу опорного сигнала приемника с фазой принимаемого сигнала. Однако при отсутствии синхронизации между передатчиком и приемником может использоваться квадратурная демодуляция. Как было только что сказано, наихудшее фазовое расхождение составляет ±90°. Таким образом, если мы выполняем умножение с двумя опорными сигналами, разделенным по фазе на 90°, выходной сигнал одного умножителя компенсирует уменьшающуюся амплитуду выходного сигнала другого умножителя. В этом случае наихудшая разность фаз составляет 45°, и вы можете видеть на приведенной выше диаграмме, что разность фаз 45° не приводит к катастрофическому уменьшению амплитуды демодулированного сигнала.
Следующие диаграммы демонстрируют эту I/Q компенсацию. Графики являются демодулированными сигналами от ветвей I и Q квадратурного демодулятора.
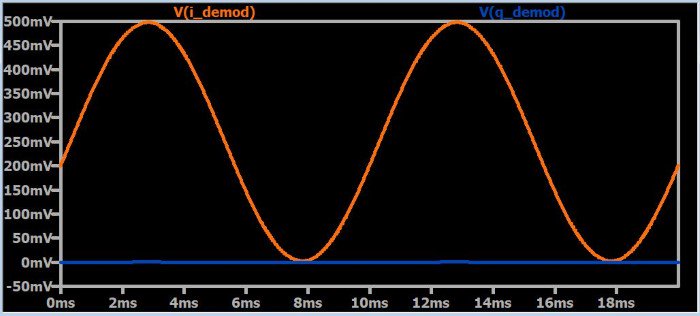
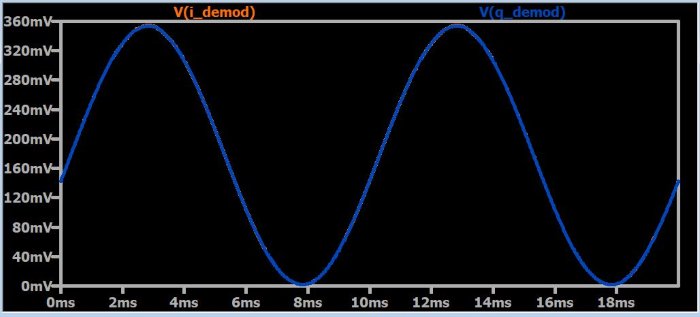
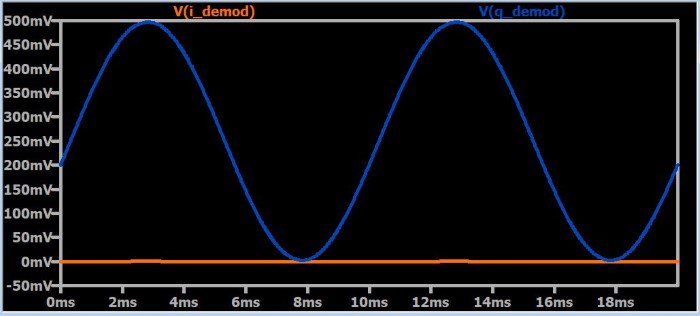
Постоянная амплитуда
Было бы удобно, если бы мы могли объединить I и Q версии демодулированного сигнала в один сигнал, который поддерживает постоянную амплитуду независимо от соотношения фаз между передатчиком и приемником. Ваша первая идея может заключаться в использовании сложения, но, к сожалению, это не так просто. Следующая диаграмма была получена путем повторения моделирования, в котором всё одинаково, за исключением фазы сигнала несущей передатчика. Значение фазы присваивается параметру, который имеет семь определенных значений: 0°, 30°, 60°, 90°, 120°, 150° и 180°. Графики представляют собой суммы демодулированных I и Q сигналов.
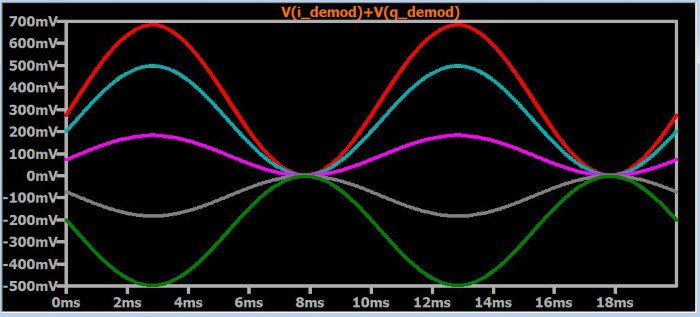
Как вы можете видеть, сложение, разумеется, не является способом получения сигнала, на который не влияют изменения в отношении фаз между передатчиком и приемником. И это неудивительно, если вспомнить математическую равнозначность между I/Q сигналами и комплексными числами: I и Q компоненты сигнала аналогичны действительной и мнимой частям комплексного числа. Выполняя квадратурную демодуляцию, мы получаем реальные и мнимые компоненты, которые соответствуют амплитуде и фазе низкочастотного сигнала. Другими словами, I/Q демодуляция, по сути, является преобразованием: мы переводим из системы «амплитуда-плюс-фаза» (используемой типовым низкочастотным сигналом) в декартову систему, в которой компонент I нанесен на ось x, а компонент Q нанесен на ось y.
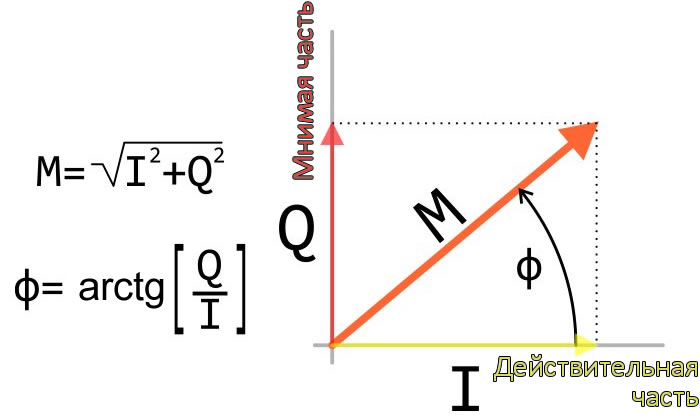
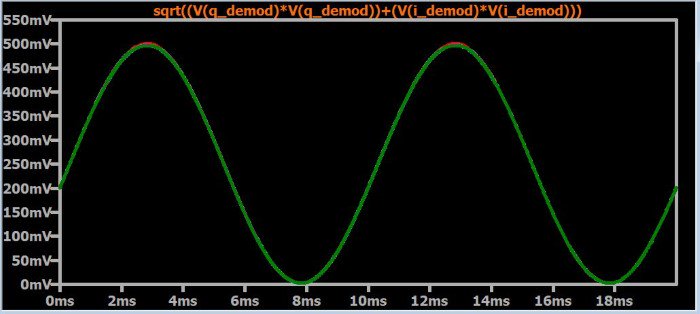
Чтобы получить амплитуду комплексного числа, мы не можем просто сложить действительную и мнимую части, и то же самое относится к I и Q компонентам сигнала. Вместо этого мы должны использовать формулу, показанную на рисунке выше, которая представляет собой не что иное, как стандартный пифагоров подход к определению длины гипотенузы прямоугольного треугольника. Если мы применим эту формулу к демодулированным сигналам I и Q, то сможем получить окончательный демодулированный сигнал, на который не влияют изменения фазы. Следующий график подтверждает это: моделирование такое же, как и предыдущее (т.е. семь разных значений фазы), но вы видите только один сигнал, потому что все графики идентичны.
Резюме
- Квадратурная демодуляция использует два опорных сигнала, разделенных по фазе на 90°, вместе с двумя умножителями и двумя фильтрами нижних частот, чтобы генерировать демодулированные сигналы I и Q.
- Квадратурная демодуляция может использоваться для создания амплитудного демодулятора, который не требует фазовой синхронизации между передатчиком и приемником.
- Сигналы I и Q, полученные в результате квадратурной демодуляции, эквивалентны действительной и мнимой частям комплексного числа.
