Как демодулировать цифровую фазовую модуляцию
Рассмотрим, как извлечь исходные цифровые данные из сигнала фазовой манипуляции.
В двух предыдущих статьях мы обсудили, системы демодуляции сигналов AM и FM, которые переносят аналоговые данные, такие как (неоцифрованный) аудиосигнал. Теперь мы готовы посмотреть, как восстановить исходную информацию, которая была закодирована с помощью третьего типа модуляции, а именно фазовой модуляции.
Однако аналоговая фазовая модуляция не является общепринятой, в то время как цифровая фазовая модуляция очень распространена. Таким образом, имеет смысл исследовать фазовую модуляцию (ФМ, англ. PM) в контексте цифровой радиосвязи. Мы рассмотрим эту тему, используя двоичную фазовую манипуляцию (BPSK); однако важно знать, что квадратурная фазовая манипуляция (QPSK) более актуальна для современных беспроводных систем.
Как следует из названия, двоичная фазовая манипуляция представляет цифровые данные, назначая одну фазу для логического 0 и другую фазу для логической 1. Для оптимизации точности демодуляции эти две фазы разделены на 180° – большее разделение между этими двумя значениями фазы облегчает декодирование символов.
Умножить и интегрировать... и синхронизировать
BPSK демодулятор состоит в основном из двух функциональных блоков: умножителя и интегратора. Эти два компонента будут создавать сигнал, который соответствует исходным двоичным данным. Однако также необходима схема синхронизации, поскольку приемник должен иметь возможность идентифицировать границу между периодами битов. Это важное различие между аналоговой и цифровой демодуляциями, поэтому давайте рассмотрим его более подробно.
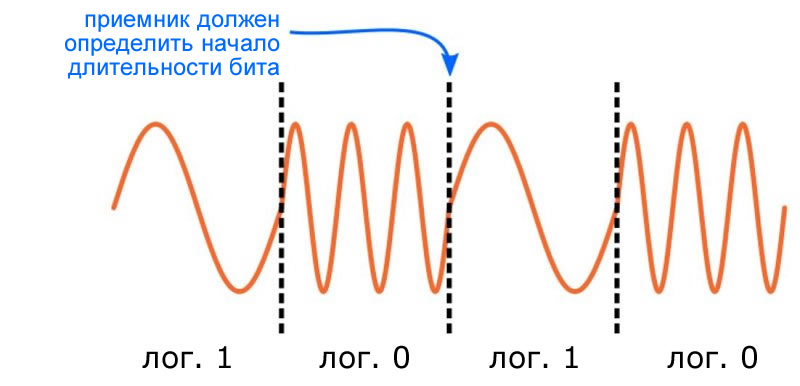
В аналоговой демодуляции сигнал фактически не имеет ни начала, ни конца. Представьте себе FM передатчик, который передает аудиосигнал, то есть сигнал, который непрерывно изменяется в зависимости от музыки. Теперь представьте FM приемник, который был изначально выключен. Пользователь может включить приемник в любой момент времени, и схема демодуляции начнет из модулированной несущей извлекать аудиосигнал. Выделенный сигнал может быть усилен и отправлен на динамик, и музыка будет звучать нормально. Приемник не имеет понятия, представляет ли собой аудиосигнал начало или конец песни, или начала ли схема демодуляции работать в начале отсчета ритма, прямо в момент удара такта или между ударами. Это не имеет значения; каждое мгновенное значение напряжения соответствует одному точному моменту в аудиосигнале, и звук воссоздается, когда все эти мгновенные значения проходят последовательно.
С цифровой модуляцией ситуация совершенно иная. Мы имеем дело не с мгновенными амплитудами, а скорее с амплитудой, которая представляет собой одну дискретную часть информации, а именно число (единица или ноль). Каждая последовательность амплитуд (по продолжительности равная периоду одного бита и называемая символом) должна отличаться от предыдущей и последующих последовательностей. Что произошло бы, если бы вещатель (из предыдущего примера) использовал цифровую модуляцию, а приемник включался и начинал демодуляцию в случайный момент времени? Ну, если бы приемник начал демодулировать в середине символа, то он попытался бы интерпретировать половину одного символа и половину следующего символа. Это, конечно, приведет к ошибкам; символ логической единицы, за которым следует символ логического нуля, будет иметь равные шансы быть интерпретированным и как единица, и как ноль.
Очевидно, что тогда в любой цифровой радиочастотной системе приоритетной должна быть синхронизация. Один простой подход к синхронизации заключается в передаче перед каждым пакетом предопределенной «обучающей последовательности», состоящей из чередующихся символов нулей и символов единиц (как на диаграмме, приведенной выше). Приемник может использовать эти переходы один-ноль-один-ноль, чтобы идентифицировать временную границу между символами, а затем остальные символы в пакете могут быть правильно интерпретированы путем применения предопределенной длительности символа системы.
Эффект умножения
Как упоминалось выше, фундаментальным шагом в демодуляции PSK является умножение. Более конкретно, мы умножаем входящий PSK сигнал на опорный сигнал с частотой, равной несущей частоте. Что это дает? Давайте посмотрим на математику; во-первых, это произведение двух функций синуса:
\[\sin(x)*\sin(y)=\frac{1}{2} \left( \cos(x-y)-\cos(x+y) \right)\]
Если мы рассмотрим эти обобщенные функции синуса как сигналы с частотой и фазой, то получим следующее:
\[\sin(\omega_{нес}+\theta_1)*\sin(\omega_{нес}+\theta_2)= \frac{1}{2} \left[ \cos(\omega_{нес}+\theta_1-(\omega_{нес}+\theta_2))- \cos(\omega_{нес}+\theta_1+\omega_{нес}+\theta_2) \right]\]
Упростив это выражение, мы получим:
\[\sin(\omega_{нес}+\theta_1)*\sin(\omega_{нес}+\theta_2)= \frac{1}{2} \left[ \cos(\theta_1-\theta_2)-\cos(2\omega_{нес}+(\theta_1+\theta_2)) \right]\]
Поэтому, когда мы умножаем две синусоиды одинаковой частоты, но с разными фазами, результатом является синусоида удвоенной частоты плюс смещение, которое зависит от разности между этими двумя фазами. Смещение здесь является ключевым показателем. Если фаза принимаемого сигнала равна фазе опорного сигнала, мы имеем cos(0°), который равен 1. Если фаза принимаемого сигнала на 180° отличается от фазы опорного сигнала, мы имеем cos(180°), который равен –1. Таким образом, выходной сигнал умножителя будет иметь положительное смещение по напряжению для одних двоичных значений и отрицательное смещение по напряжению для других двоичных значений. Это смещение может использоваться для интерпретации каждого символа как нуля или единицы.
Подтверждение с помощью моделирования
Следующая схема модуляции и демодуляции BPSK показывает, как вы можете создать BPSK сигнал в LTspice:
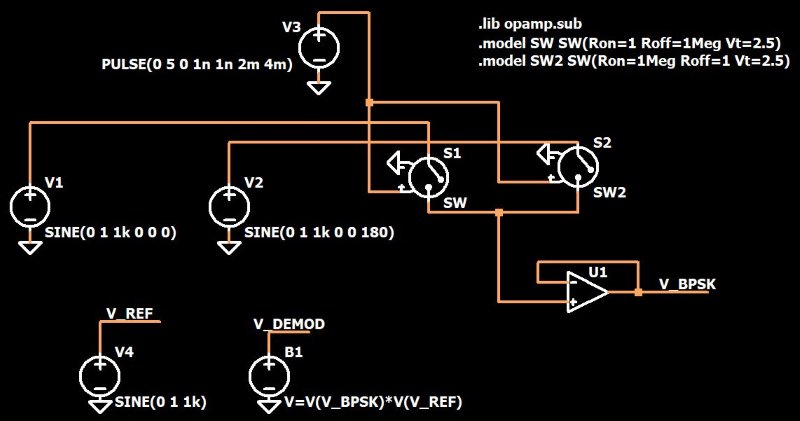
Два источника синусоидального напряжения (один с фазой = 0°, и один с фазой = 180°) подключены к двум коммутаторам, управляемым напряжением. Оба коммутатора управляются одним и тем же прямоугольным сигналом, но их сопротивления включения и выключения настроены так, что, когда один разомкнут, другой замкнут. «Выходные» выводы этих двух коммутаторов соединены вместе, а операционный усилитель выполняет роль буфера для полученного сигнала, который выглядит следующим образом:
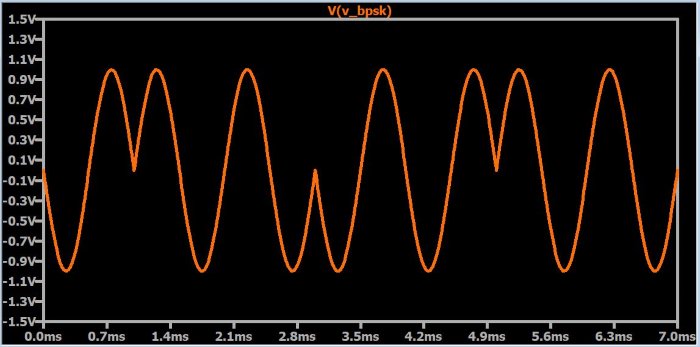
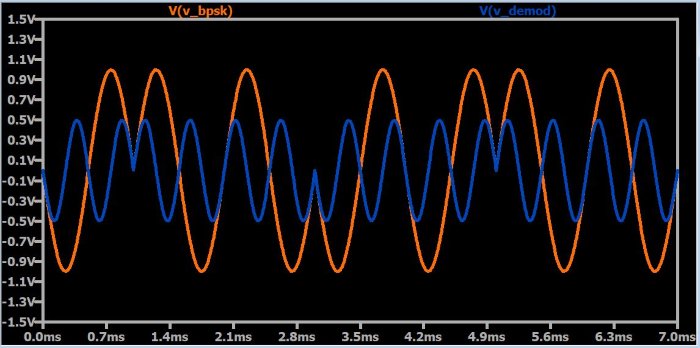
Далее мы добавляем опорную синусоиду (V4) с частотой, равной частоте BPSK сигнала, и используем источник напряжения с произвольным поведением для умножения BPSK сигнала на опорный сигнал. Ниже показан результат:
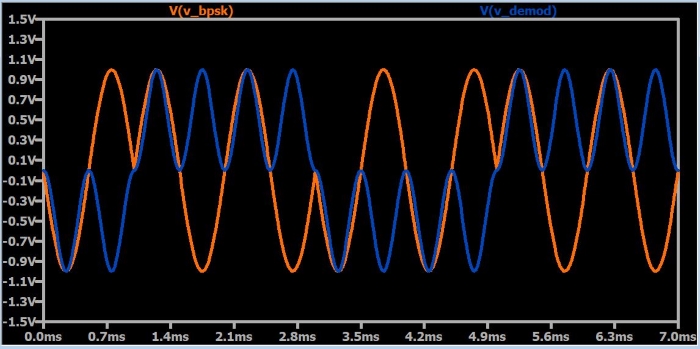
Как вы можете видеть, демодулированный сигнал удваивает частоту принимаемого сигнала и имеет положительное или отрицательное смещение по напряжению в соответствии с фазой каждого символа. Если затем проинтегрировать этот сигнал относительно длительности каждого бита, мы получим цифровой сигнал, который соответствует исходным данным.
Когерентное детектирование
В этом примере фаза опорного сигнала приемника синхронизирована с фазой входного модулированного сигнала. Это легко выполнить при моделировании, но значительно сложнее в реальной жизни. Кроме того, как обсуждалось на этой странице в разделе «Дифференциальное кодирование», обычная фазовая манипуляция не может использоваться в системах, которые подвержены непредсказуемым разностям фаз между передатчиком и приемником. Например, если опорный сигнал приемника находится по фазе на 90° относительно сигнала несущей передатчика, разность фаз между опорным сигналом и BPSK сигналом всегда будет равна 90°, а cos(90°) равен 0. Таким образом, смещение по напряжению будет потеряно, и система будет полностью неработоспособной.
Это можно подтвердить, изменив фазу источника V4 на 90°, ниже показан результат:
Резюме
- Цифровая демодуляция требует синхронизации по длительности бита, так как приемник должен иметь возможность идентифицировать границы между соседними символами.
- Сигналы двоичной фазовой манипуляции могут быть демодулированы посредством умножения с последующим интегрированием. Опорный сигнал, используемый на этапе умножения, имеет ту же частоту, что и сигнал несущей передатчика.
- Обычная фазовая манипуляция надежна, только когда фаза опорного сигнала приемника может поддерживать синхронизацию с фазой сигнала несущей передатчика.
