Отрицательная обратная связь, часть 9: разрыв петли

Простая методика моделирования «с разрывом петли обратной связи» обеспечивает удобный анализ устойчивости, особенно в случае сложных схем. Рассмотрим ее.

Вспомогательная информация

• Введение в операционные усилители
• Операционные усилители: отрицательная обратная связь
• Фаза сигнала переменного тока

Неуловимое петлевое усиление

Вы, возможно, уже поняли, что в анализе устойчивости есть что-то слегка неприятное – почему-то он не так прост, как должен быть. После некоторого размышления вы, вероятно, определили источник этого неудобства: петлевое усиление. Как мы теперь хорошо знаем, устойчивость в основном зависит от частотной характеристики петлевого усиления Aβ; проблема заключается в том, что петлевое усиление не является измеримой или даже интуитивно понятной величиной в реальных схемах. Коэффициент усиления без обратной связи A является интуитивно понятной и измеримой величиной: подайте тестовый сигнал на сам усилитель без обратной связи и измерьте выходной сигнал. Аналогично, коэффициент усиления с обратной связью интуитивно понятен и измерим: соберите (или смоделируйте) схему и измерьте выходной сигнал относительно входного. Петлевое усиление, напротив, «скрыто» внутри наблюдаемых извне напряжений и токов.

Так что же происходит, когда вам нужно исследовать устойчивость сложного усилителя с обратной связью? Или что, если вам просто не нравится некий «ручной» подход, принятый в предыдущих статьях, где мы рассматривали цепь обратной связи как частично отдельную цепь и объединяли напряжение обратной связи с амплитудно-частотной характеристикой усилителя без обратной связи для создания необходимых графиков для анализа устойчивости? Что ж, оказывается, что существует четко определенный метод извлечения петлевого усиления из существующей схемы.

Разорванная петля

На следующей диаграмме показана общая структура обратной связи, представленная в первой статье, но с одним важным изменением: цепь обратной связи была оторвана от выхода, и в точку разрыва подан тестовый сигнал.

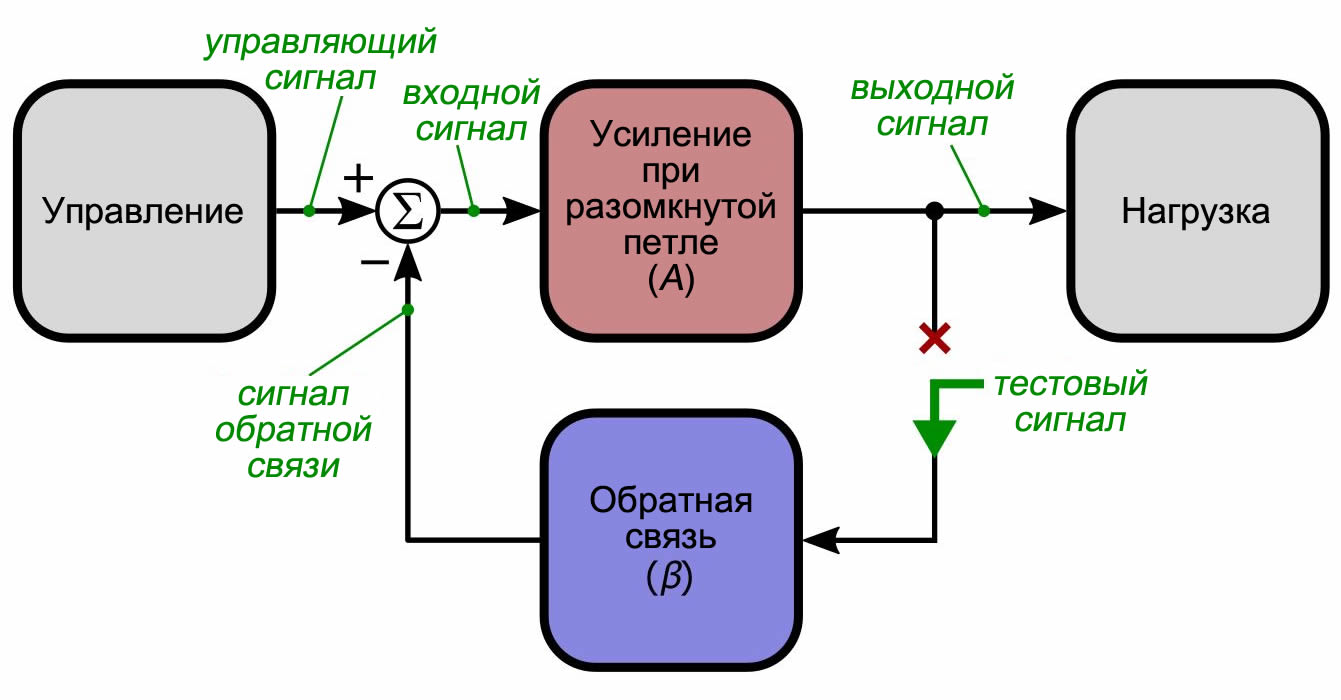
Если вы удалите (т. е. установите на ноль) входной сигнал из всей системы (здесь обозначен как элемент управление), а затем проанализируете поток сигналов через эту новую структуру, вы увидите, что в игру вступают следующие отношения:

\[\text{входной_сигнал}=0-\beta\times\text{тестовый_сигнал} \Rightarrow\\ \Rightarrow\ \text{выходной_сигнал}=-A\beta\times\text{тестовый_сигнал} \Rightarrow\\ \Rightarrow\ \ \frac{\text{выходной_сигнал}}{\text{тестовый_сигнал}}=-A\beta\]

В наших симуляциях мы всегда будем использовать тестовое напряжение 1 В, поэтому мы можем упростить это выражение следующим образом:

\[A\beta=-\text{выходной_сигнал}\]

Таким образом, когда мы разрываем петлю обратной связи и вводим тестовый сигнал 1 В в цепь обратной связи, выходной сигнал усилителя, умноженный на минус 1, представляет собой петлевой коэффициент усиления. Теоретически этот подход может быть использован для исследования петлевого усиления с помощью математического анализа, моделирования или даже реальной схемы вместе с тестовым сигналом с изменяющейся частотой. Но с математическим и измерительным подходами возникают практические трудности, прежде всего потому, что теоретически необходимо нагрузить разорванную петлю импедансом, эквивалентным импедансу, существовавшему до разрыва петли. Поэтому без дальнейших церемоний мы перейдем к использованию этого метода на основе моделирования. На самом деле, в данном контексте моделирование обычно (если не всегда) это наименее утомительный и наиболее информативный подход.

Еще один полюс, о котором стоит побеспокоиться

Из предыдущих статей мы знаем, что полюсы могут создавать проблемы тем, кому нужны устойчивые усилители. Операционные усилители с внутренней компенсацией имеют один полюс, доминирующий на частотной характеристике, что обеспечивает устойчивость в большинстве ситуаций. Но полюс в цепи обратной связи, созданный емкостью, параллельной резистору обратной связи, может обеспечить дополнительный сдвиг фазы, достаточный, чтобы ухудшить устойчивость. К сожалению, есть другое место, где (часто непреднамеренная) емкость может вызывать колебания, а именно – в выходном узле операционного усилителя:

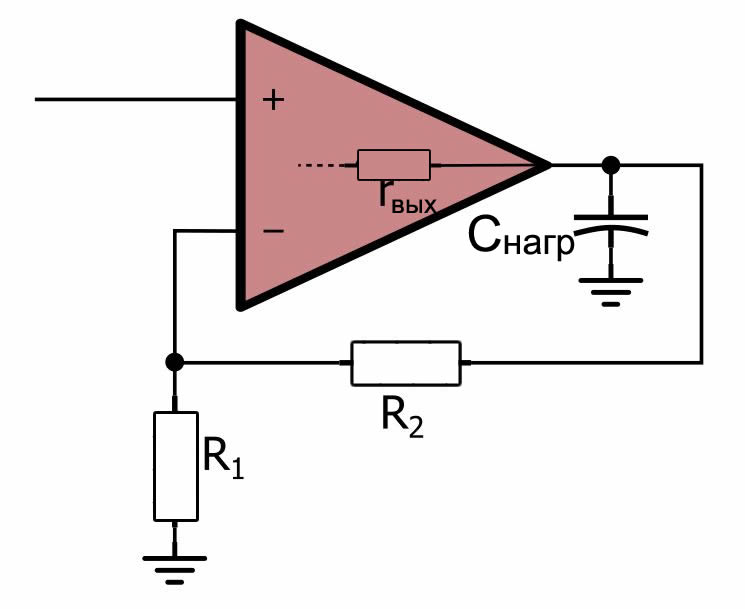
Как видите, любая емкость нагрузки, подключенная непосредственно к выходу, в сочетании с выходным сопротивлением операционного усилителя (небольшим, но ненулевым) образует RC-цепь – иными словами, однополюсный фильтр нижних частот, который дает дополнительные 90° сдвига фазы к частотной характеристике петлевого усиления.

Конечно, всегда есть хотя бы небольшое количество паразитной емкости. Сколько емкости нагрузки потребуется, чтобы реально сделать схему неустойчивой? Самый простой способ определить это – проверить техническое описание, в котором должно быть указано, какую емкость нагрузки можно безопасно использовать для конкретного операционного усилителя. Техническое описание может предоставить для этого числовую спецификацию или график, показывающий процент перерегулирования (выбросов) для различных значений емкости нагрузки. Вот пример последнего, взятый из технического описания операционного усилителя AD8505 производства Analog Devices:

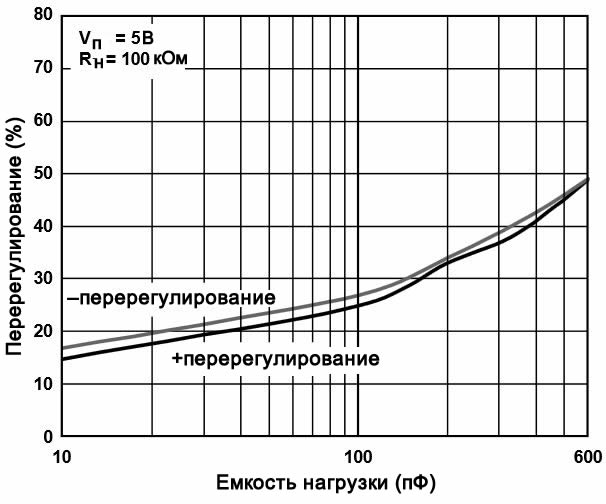
Перерегулирование (амплитуда выбросов), превышающее приблизительно 20%, указывает на недостаточный запас по фазе, поэтому для AD8505 настолько маленькая емкость нагрузки, как 30 пФ, будет уже достаточной, чтобы вызывать беспокойство.

Методика

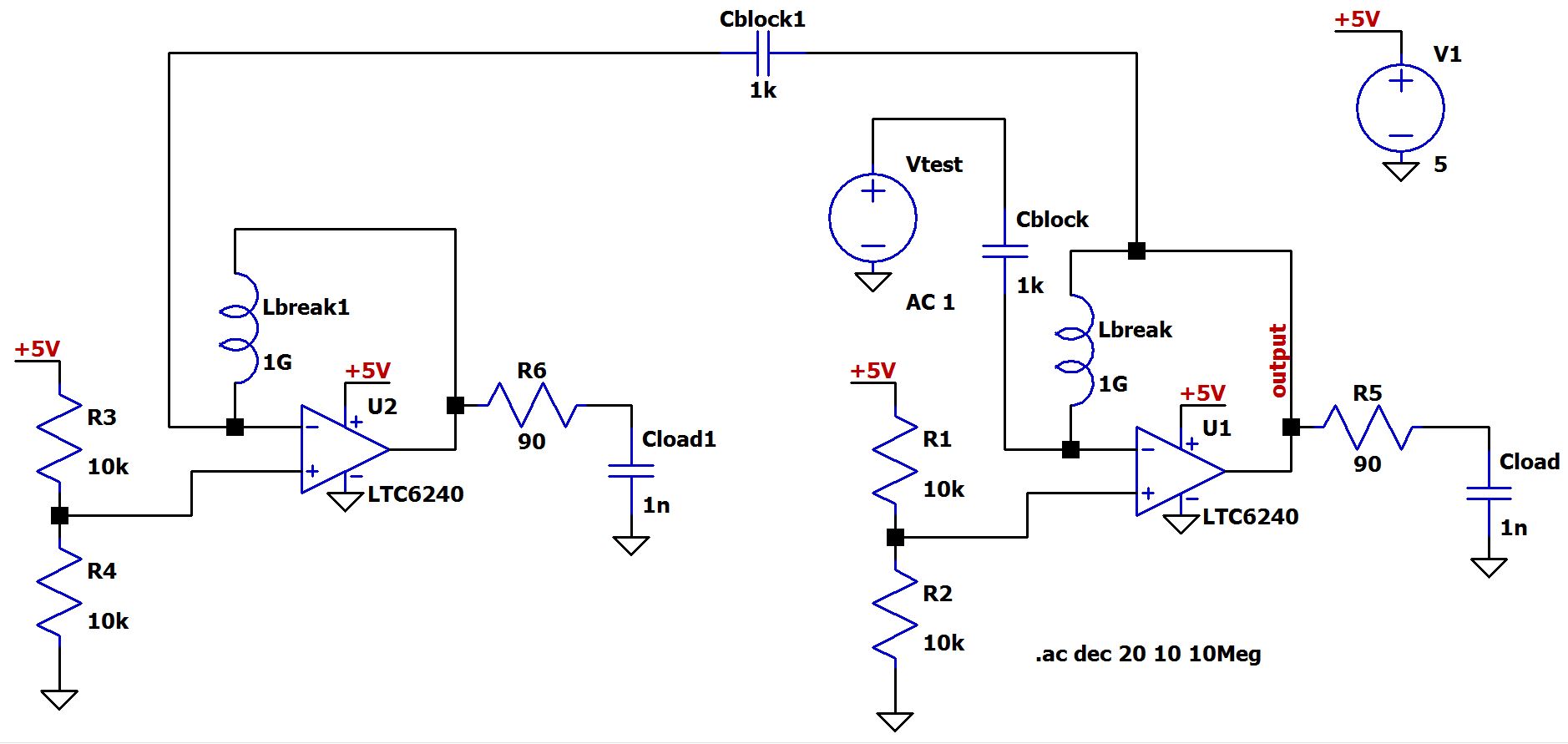
Давайте предположим, что мы используем ОУ для обеспечения опорного напряжения, равного V_DD/2, следующим образом:

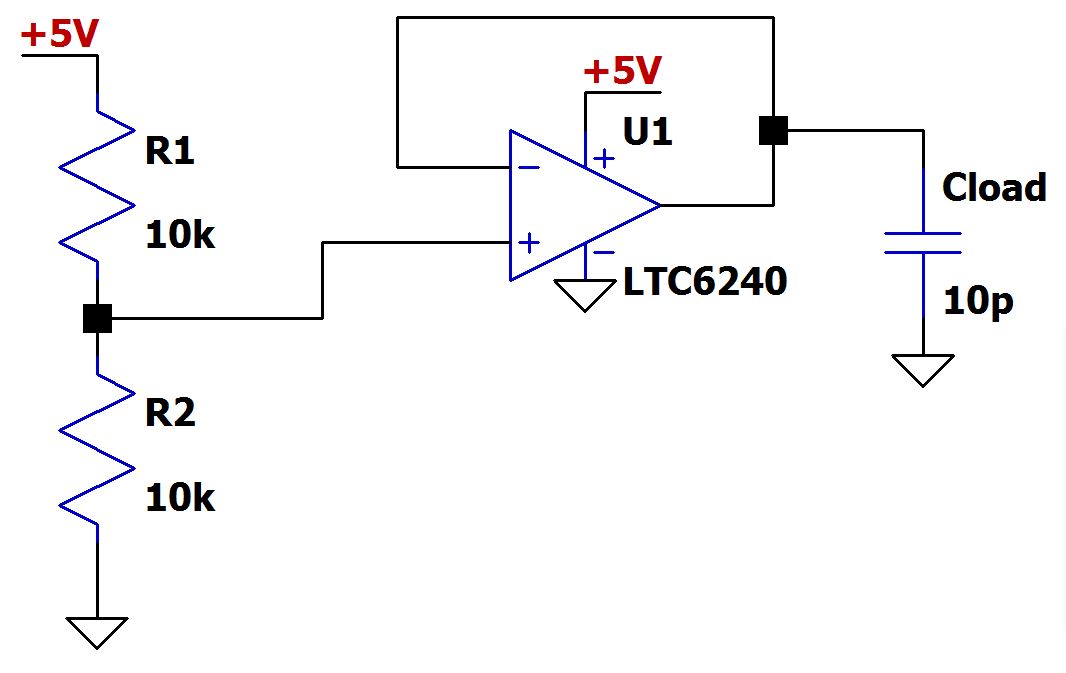
Текущее значение C_нагр представляет собой паразитную емкость. Давайте проверим устойчивость этой схемы, используя подход «разрыв петли». Мы должны убедиться, что симулятор может установить правильные условия смещения по постоянному напряжению, поэтому мы разрываем петлю, не разрывая цепь, с помощью очень большой индуктивности (1 ГГн). Эта нереально большая индуктивность с теоретическим импедансом, равным нулю при постоянном токе, обеспечивает правильное смещение по постоянному напряжению, одновременно эффективно блокируя все представляющие интерес сигналы переменного тока. Точно так же мы подаем тестовый сигнал 1 В переменного напряжения через большой конденсатор, который блокирует постоянный ток, но, по сути, не представляет импеданса для сигналов переменного тока.

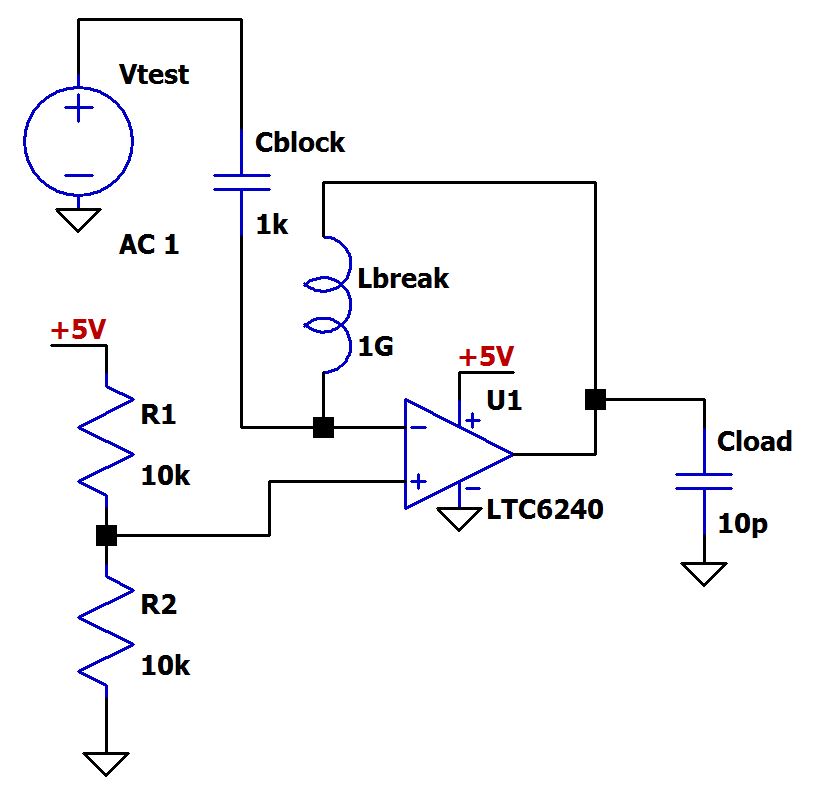
Мы еще не закончили... нам еще нужно нагрузить цепь обратной связи импедансом, который был до того, как мы разорвали петлю. Для этого есть простой, хотя и не элегантный способ: скопировать и вставить всю схему и использовать этот дубликат в качестве фиктивной нагрузки; поскольку это та же схема, она обеспечит правильный нагрузочный импеданс.

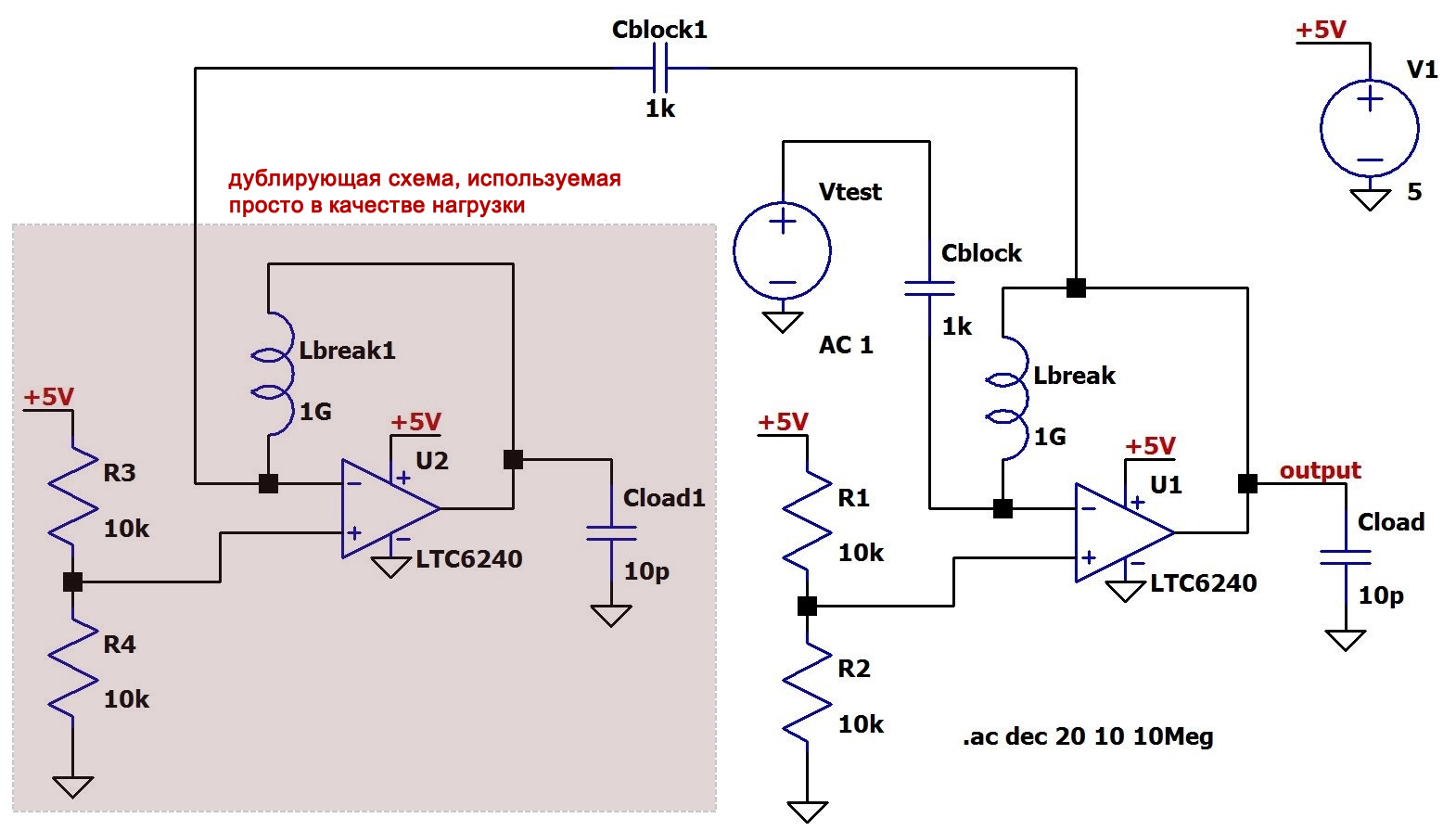
Как видите, исходный узел обратной связи подключен к узлу разрыва через другой большой конденсатор, чтобы обеспечить взаимодействие по переменному току при сохранении условий смещения по постоянному напряжению.

Теперь мы готовы к моделированию. Всё, что нам нужно сделать, это вывести V_выход.

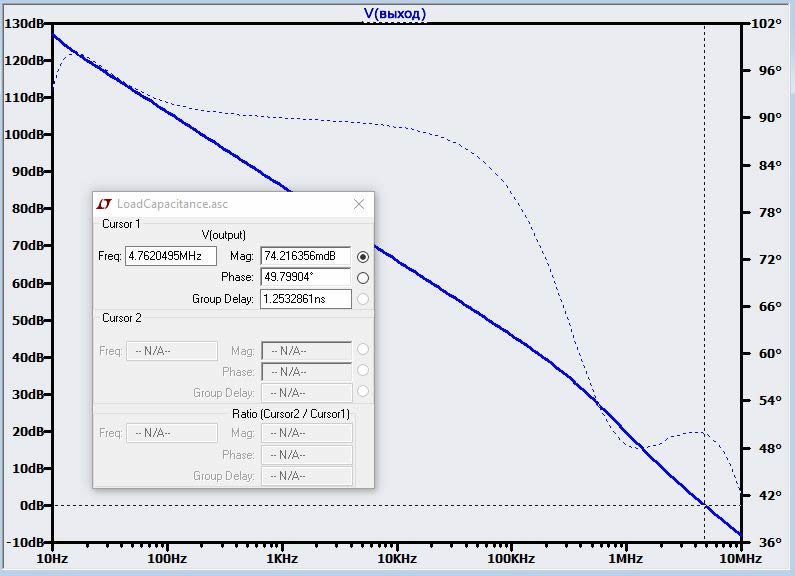
Напомним, что метод разрыва петли приводит к Aβ = -выходной_сигнал. Знак минуса соответствует сдвигу фазы на 180°, и это оказывается очень удобным: фаза начинается при 180° и приближается к нулю, что означает, что запас по фазе измеряется относительно 0°, а не 180°. Следовательно, на этом графике V_выход, если вы переместите курсор на частоту с единичным усилением, значение, указанное в поле «Phase» (фаза), представляет собой запас по фазе:

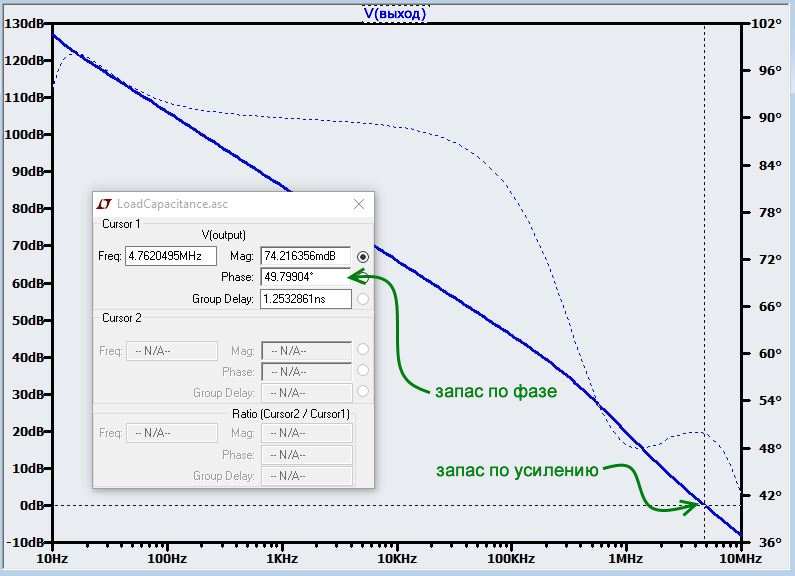
Как и ожидалось, этот операционный усилитель с внутренней компенсацией при такой небольшой емкости нагрузки полностью устойчив. Но, в конечном счете, мы решили, что нашему источнику опорного напряжения необходим дополнительный блокировочный конденсатор, поэтому мы добавим 1 нФ конденсатор на выход ОУ (не забудьте изменить конденсатор нагрузки в дублирующей схеме). Вот новый график -Aβ.

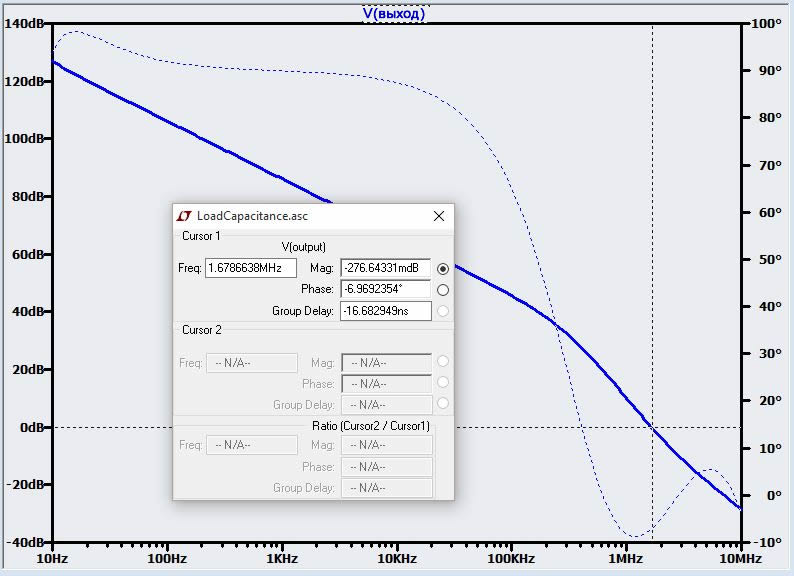
Теперь у нас есть проблема. Запас по фазе уменьшился ниже 0°, что означает, что схема теперь совершенно устойчива (а не просто не достаточно устойчива). Существуют различные методы повышения устойчивости схем на операционных усилителях с большой емкостной нагрузкой; эта обширная тема выходит за рамки этой статьи. Здесь мы фокусируемся на анализе устойчивости, поэтому мы просто продемонстрируем эффект от одного простого, распространенного средства: установки последовательного резистора между выходом операционного усилителя и конденсатором нагрузки. Резистор создает ноль в передаточной функции обратной связи, и сдвиг фазы от этого нуля несколько компенсирует проблемный сдвиг фазы, создаваемый полюсом. Резистор должен иметь такой номинал, чтобы частота нуля была достаточно низкой, чтобы обеспечить адекватное восстановление фазы. Для этой схемы мы можем выбрать резистор в соответствии с информацией, приведенной в техническом описании для LTC6240:

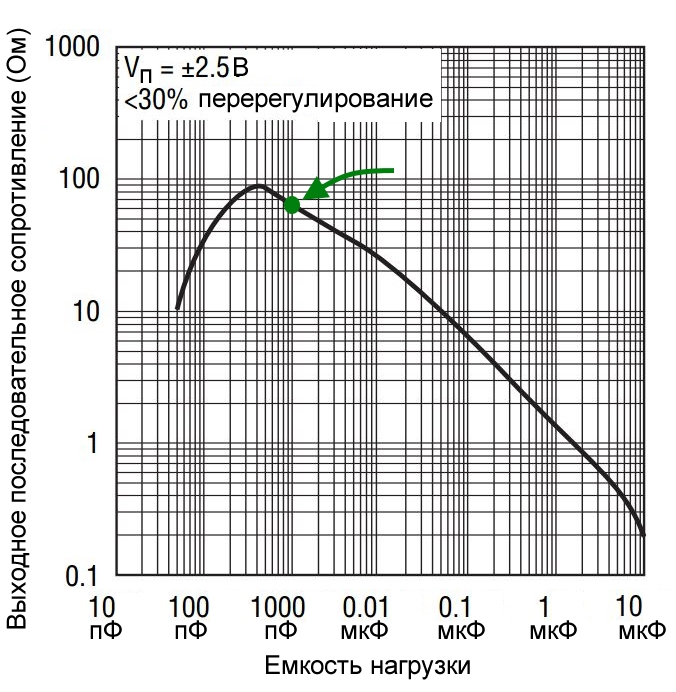
Эти значения для перерегулирования (выбросов) 30%, но нам нужно что-то ближе к перерегулированию на 20%, поэтому мы попробуем 90 Ом:

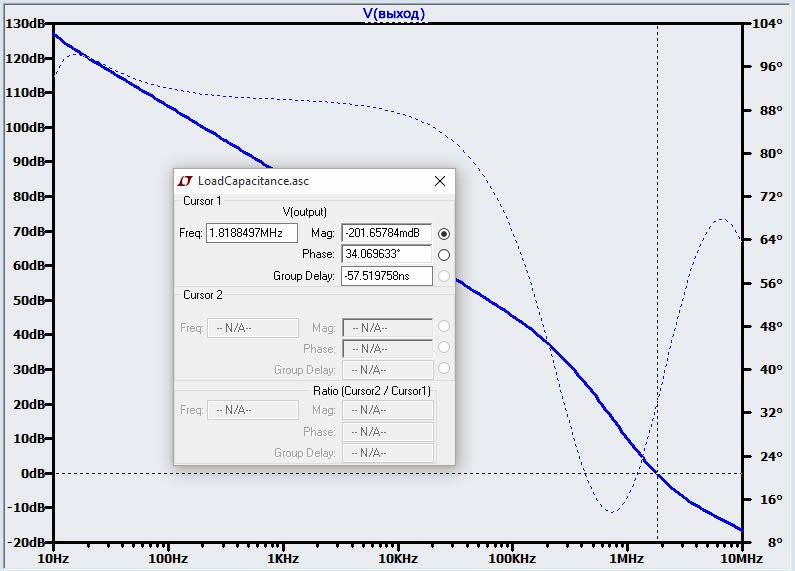
Теперь у нас есть запас по фазе 34°, немного низковат, но, вероятно, достаточен. Чтобы довести запас по фазе до 45°, потребуется последовательное сопротивление около 130 Ом.

Заключение

Теперь в вашем аналитическом наборе инструментов есть метод моделирования, который может предоставить точную и удобную информацию об устойчивости для широкого спектра схем с отрицательной обратной связью, от простых буферов на операционных усилителях до сложных топологий усилителей на дискретных транзисторах. В следующей статье мы завершим эту серию исследованием устойчивости посредством моделирования во временной области, а не в частотной области.

Теги