Отрицательная обратная связь, часть 1: общая структура и основные понятия

Данная статья, первая в серии, познакомит вас с основными понятиями, необходимыми для понимания и анализа усилителей с отрицательной обратной связью.

Не только операционные усилители...

В данной статье мы представим общую структуру отрицательной обратной связи и параметры, которые помогут нам проанализировать и реализовать эту структуру. Более конкретно, мы сосредоточимся на усилителе с отрицательной обратной связью. Термин «усилитель» здесь немного вводит в заблуждение: эта структура не ограничивается простым увеличением амплитуды сигнала. Этот «усилитель» может представлять собой систему с единичным усилением, которая предназначена для улучшения характеристик входного или выходного импеданса схемы, или это может быть фильтр, который усиливает определенные частоты при ослаблении других.

Почему обратная связь?

У нас есть выходная переменная некоторого вида, которой нужно управлять, но связь между управляющим входным параметром и фактическим поведением выходного параметра настолько сложна или непредсказуема, что было бы трудно, если не невозможно, точно регулировать выходной параметр просто используя заданный входной параметр. Рассмотрим два примера: у нас есть цифро-аналоговый преобразователь (ЦАП, DAC) с выходным напряжением, и мы хотим управлять 1) мощностью, рассеиваемой резистором, и 2) яркостью светодиода. Первая задача не требует отрицательной обратной связи, потому что связь между входным и выходным параметрами проста и предсказуема:

\[P= \frac{V^2}{R}, \qquad V=\sqrt{PR}\]

Всё, что нам нужно сделать, это умножить желаемую мощность на сопротивление и затем взять квадратный корень. Это довольно простая математика для современного микроконтроллера, и, что более важно, это соотношение справедливо для любого резистора в любых условиях окружающей среды.

Но вторая задача не так проста. Вот график зависимости прямого тока от прямого напряжения для светодиода производства Avago:

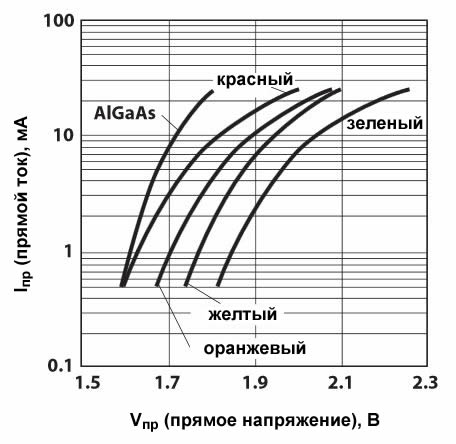
Связь очень нелинейна и существенно зависит от типа светодиода; и хотя это и не показано на графике, эта связь также зависит от температуры. Теперь посмотрим на зависимость яркости от тока в прямом направлении:

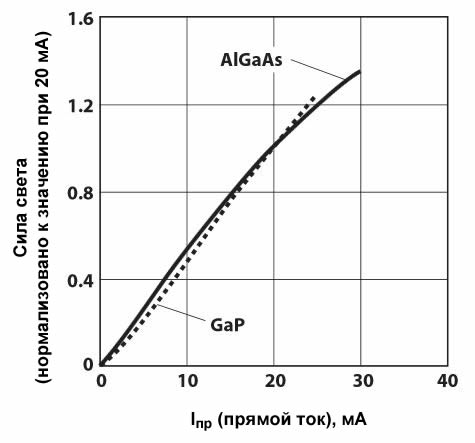
Эта связь довольно линейна, с минимальной разницей между двумя полупроводниковыми материалами. Итак, какой мы делаем из этого вывод? Было бы довольно просто точно регулировать яркость светодиодов, контролируя ток, и было бы довольно сложно точно регулировать яркость, контролируя напряжение. Что делать? Добавьте отрицательную связь! Мы могли бы использовать напряжение ЦАП в качестве входного сигнала для усилителя с отрицательной обратной связью, который регулирует свое выходное напряжение в зависимости от того, какой ток протекает через светодиод (актуальная информация может быть измерена с помощью последовательного резистора). Теперь у нас есть простая, предсказуемая связь между напряжением и яркостью.

Этот пример со светодиодом является одной из бесчисленных ситуаций, в которых было бы нежелательно или совершенно нецелесообразно реализовывать управление с разомкнутой петлей (т. е. без обратной связи). Подумайте о регулировании температуры: как управление с разомкнутой петлей может учитывать все факторы, влияющие, например, на жилую комнату? Погодные условия, окна, двери, количество жильцов... Но, как показывает повсеместное использование простого термостата, с небольшой отрицательной обратной связью эта проблема становится почти тривиальной.

Абстрактный усилитель с обратной связью

Когда вы посмотрите на эту диаграмму, постарайтесь уделить минуту, чтобы оценить элегантность отрицательной обратной связи.

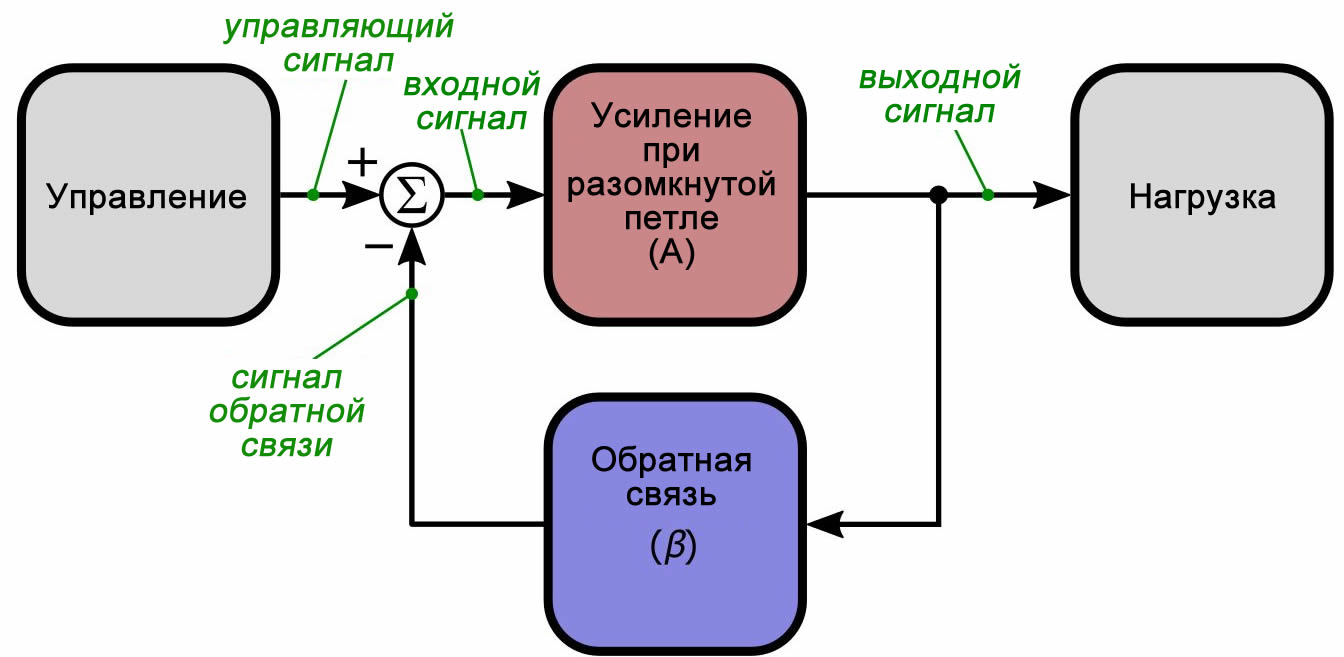
Путем простого вычитания фактического значения выходного параметра (умноженного на β) из опорного сигнала, и используя результат в качестве входного сигнала усилителя с разомкнутой петлей, мы можем точно управлять нагрузкой, даже когда связь вход→выход является несовместимой или сложной.

Ключевыми параметрами здесь являются A и β. Зеленые надписи курсивом представляют название переменных для сигналов, проходящих через систему; в тексте статьи мы также используем слова (также выделенные курсивом) вместо переменных, обозначенных буквами, в надежде, что предстоящий анализ не будет казаться менее интуитивным, чем на самом деле. (Мы сохраняем A и β, потому что усилитель с обратной связью без A и β просто не будет усилителем с обратной связью.)

Так что же такое А и β? Об А сказать особо нечего: это усиление, которое вся система применила бы при отсутствии обратной связи. В контексте схемы операционного усилителя (сравнение особенно уместно, потому что операционный усилитель является довольно прямым проявлением теоретического усилителя с обратной связью) А соответствует коэффициенту усиления операционного усилителя с разомкнутой петлей обратной связи. С β всё не совсем так просто: коэффициент обратной связи β определяет, какая часть выходного сигнала возвращается обратно в узел вычитания. Вы можете думать о β как о части (выраженной в виде дроби) выходного сигнала, которая вычитается из управляющего сигнала. Это должно стать более понятным, если вы вспомните о базовой неинвертирующей схеме на операционном усилителе:

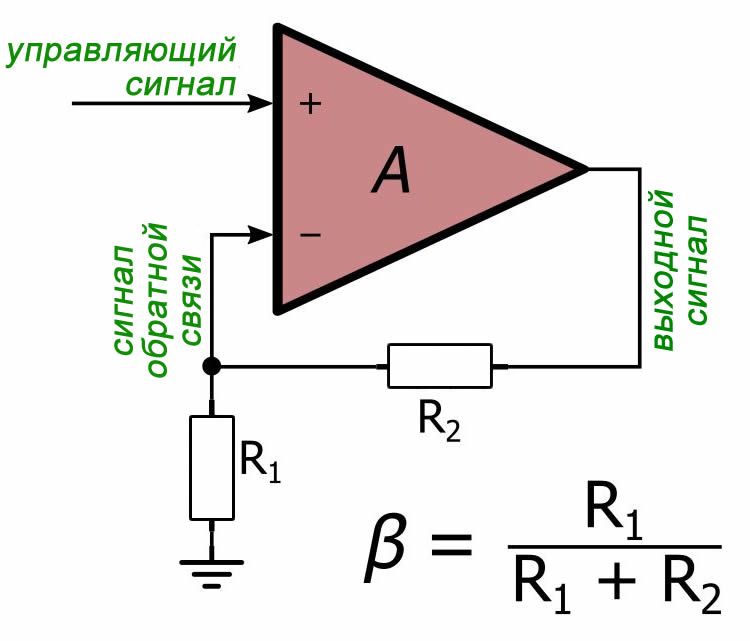
Два резистора, которые мы используем для настройки усиления, представляют собой не что иное, как делитель напряжения, который подает определенную часть выходного сигнала на инвертирующий вход операционного усилителя. Напряжение на выходе резисторного делителя выражается отношением R₁/(R₁+R₂), умноженным на напряжение на входе делителя. Таким образом, часть выходного сигнала (выраженная в виде дроби) возвращается и вычитается из управляющего сигнала, – то есть коэффициент обратной связи β составляет R₁/(R₁+R₂). Стоит потратить некоторое время на интуитивное понимание этой концепции, потому что β будет занимать важное место в следующей статье, где мы будем обсуждать стабильность.

Еще одно замечание об А и β: они не обязательно должны быть простыми константами, как, например, A = 10⁶ и β = 0,1. Они также могут быть представлены как функции от частоты, что означает, что значение A или β изменяется в зависимости от частоты сигнала, проходящего через систему усилителя. Это особенно актуально для А – усиление операционных усилителей с внутренней компенсацией при разомкнутой петле обратной связи начинает падать на частотах начиная с 0,1 Гц!

Замыкание петли

Теперь мы кратко рассмотрим некоторые существенные связи и формулы, которые помогут нам лучше понять и проанализировать поведение усилителя с обратной связью. Во-первых, это математическое определение β:

\[\text{сигнал_обратной_связи} = \beta\times \text{выходной_сигнал},\\ \beta=\frac{\text{сигнал_обратной_связи}}{\text{выходной_сигнал}}\]

Это просто выражение того, что мы описали в предыдущем разделе. Далее следует прямая взаимосвязь между входным сигналом и выходным сигналом, которая очевидна из общей структурной схемы обратной связи, показанной выше:

\[\text{выходной_сигнал} = A\times \text{входной_сигнал}\]

Несколько более интересным является формула для коэффициента усиления с замкнутой петлей обратной связи (G_ОС), то есть общий коэффициент усиления усилительной системы, когда учитывается влияние отрицательной обратной связи.

\[G_{ОС}=\frac{\text{выходной_сигнал}}{\text{управляющий_сигнал}}=\\ = \frac{A\times \text{входной_сигнал}}{\text{входной_сигнал}+\text{сигнал_обратной_связи}}= \\ = \frac{A\times \text{входной_сигнал}}{\text{входной_сигнал}+(\beta\times \text{выходной_сигнал})}=\\ = \frac{\text{входной_сигнал} \times A}{\text{входной_сигнал} \times \left(1+\beta\frac{\text{выходной_сигнал}}{\text{входной_сигнал}}\right)}=\\ = \frac{A}{1+A\beta}\]

Эти соотношения довольно просты, но становятся еще лучше. В типовых применениях усилителей с обратной связью величина Aβ (называемая «усилением петли») намного больше 1 – например, при коэффициенте усиления операционного усилителя без обратной связи 10⁶ и коэффициенте обратной связи 0,1 коэффициент усиления петли равен 10⁵. Таким образом, мы можем упростить выражение коэффициента усиления с обратной связью следующим образом:

\[G_{ОС}=\frac{A}{1+A\beta}\approx\frac{A}{A\beta}=\frac{1}{\beta}\]

И здесь мы видим именно то, что ожидаем от нашего опыта работы со схемами на операционных усилителях: усиление зависит только от β. Посмотрите еще раз на схему неинвертирующего усилителя на ОУ, показанную выше; все сходится, если вспомнить, что формула коэффициента усиления для стандартного неинвертирующего усилителя (G_неинв) – это 1+(R₂/R₁):

\[G_{неинв}=1+\frac{R_2}{R_1},\\ G_{ОС}=\frac{1}{\beta}=\frac{R_1+R_2}{R_1}=\frac{R_1}{R_1}+\frac{R_2}{R_1}=1+\frac{R_2}{R_1}\]

Заключение

После представления отрицательной обратной связи и общего описания причин ее использования мы представили теоретическую модель, которая поможет нам проанализировать конкретные характеристики усилителя с отрицательной обратной связью. Затем мы добавили немного математики, чтобы продемонстрировать наиболее заметное преимущество добавления отрицательной обратной связи – а именно: для всех практических целей общий коэффициент усиления системы полностью определяется простыми (и точными, если необходимо) внешними компонентами, составляющими цепь обратной связи. В следующей статье мы рассмотрим некоторые дополнительные способы, с помощью которых отрицательная обратная связь может улучшить производительность схемы усилителя.

Теги