Отрицательная обратная связь, часть 5: запас по усилению и запас по фазе

Рассмотрим, как использовать моделирование в частотной области для анализа петлевого усиления и оценки устойчивости схемы усилителя.

Вспомогательная информация

• Введение в операционные усилители
• Операционные усилители: отрицательная обратная связь
• Фаза сигнала переменного тока
• Введение в биполярные транзисторы

Чтобы вам не приходилось переключаться между страницами каждый раз, когда вы хотите обдумать общую структуру обратной связи, вот схема, представленная в первой статье:

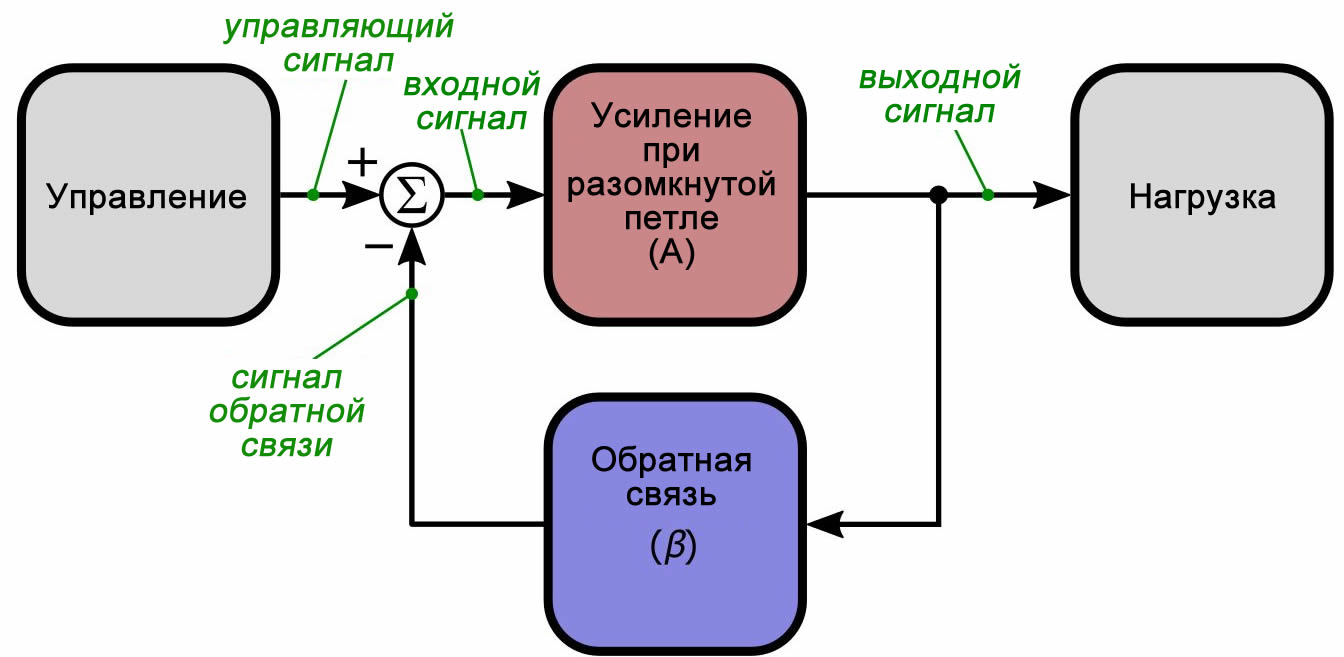
Насколько устойчив ваш усилитель?

В предыдущей статье мы видели, что решающим параметром в анализе устойчивости является петлевой коэффициент усиления (петлевое усиление), то есть частотная характеристика коэффициента усиления усилителя без обратной связи, умноженная на частотную характеристику коэффициента передачи цепи обратной связи. Если величина петлевого усиления больше единицы на f₁₈₀ (то есть частоте, на которой сдвиг фазы петлевого усиления составляет 180°), схема является неустойчивой (нестабильной). Было бы разумно сделать вывод, что схема устойчива, если при f₁₈₀ величина петлевого усиления меньше единицы, но реальная жизнь редко бывает такой простой и удобной. Как упоминалось в предыдущей статье, значения петлевого усиления, немного меньшие единицы, при f₁₈₀ приведут к граничной устойчивости, которая на самом деле может быть намного хуже, чем явная неустойчивость. Таким образом, нам нужен способ определить, является ли схема достаточно устойчивой – то есть достаточно устойчивой, чтобы гарантировать, что схема будет работать правильно, несмотря на разброс параметров заменяемых компонентов и условия окружающей среды или условия эксплуатации, которые влияют на характеристики коэффициента усиления усилителя без обратной связи или на характеристики цепи обратной связи. Здесь вступают в игру запас по усилению и запас по фазе.

Прежде чем перейти к моделированию, давайте кратко рассмотрим один важный вопрос: что, если сдвиг фазы петлевого усиления никогда не достигнет 180°? Напомним, что каждый полюс в передаточной функции схемы обеспечивает сдвиг фазы на 90°. Если схема имеет только один полюс, никакая частотная составляющая никогда не будет сдвинута по фазе более чем на 90°, и, следовательно, схема безусловно устойчива. Реальные усилители включают в себя различные источники паразитной емкости и индуктивности, поэтому настоящая однополюсная передаточная функция не очень практична. Однако схема усилителя может быть спроектирована так, чтобы иметь доминирующий низкочастотный полюс, так что коэффициент усиления без обратной связи напоминает однополюсную характеристику на большей части используемой полосы пропускания усилителя. В результате усилитель будет устойчивым в подавляющем большинстве приложений. Большинство операционных усилителей спроектированы именно таким образом – эти операционные усилители с «внутренней компенсацией» жертвуют высокочастотным усилением в пользу устойчивости.

Однажды, когда в магазинах не было тысяч различных операционных усилителей...

Для моделирования мы будем использовать дискретную схему усилителя на биполярных транзисторах. Вот схема LTSpice:

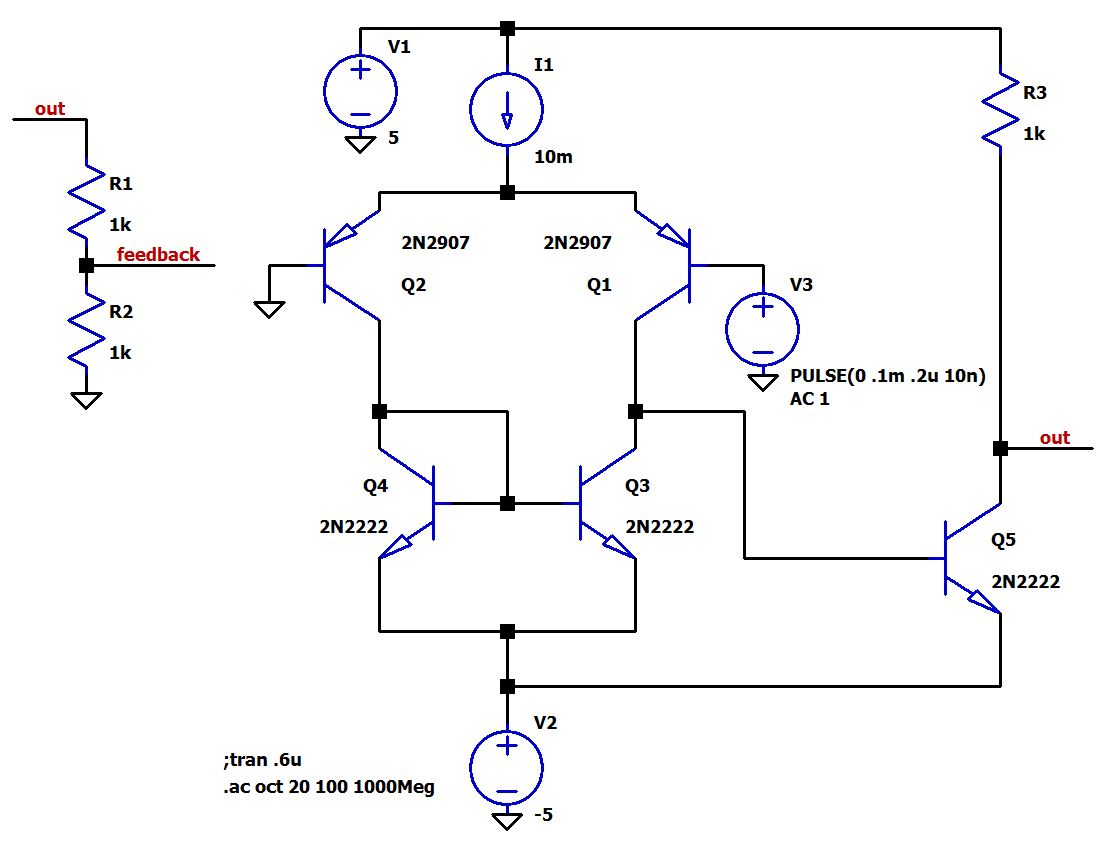
Эта простая схема лучше подойдет для моделирования переходных процессов, чем макромодели операционных усилителей LTSpice, и она удивительно неустойчива по сравнению с операционными усилителями с внутренней компенсацией. То, что вы видите здесь, по сути, является упрощенным двухкаскадным усилителем. Q₁ и Q₂ образуют дифференциальную пару с Q₃ и Q₄, работающими в качестве активной нагрузки. Это первый каскад. Второй каскад – усилитель с общим эмиттером, состоящий из Q₅ и R₃. Сопротивление R₃ выбрано так, чтобы ток коллектора Q₅ был примерно равен значению источника тока I₁, который в реальной схеме был бы реализован как токовое зеркало. В настоящее время схема настроена для моделирования коэффициента усиления без обратной связи, поскольку инвертирующий вход (слева) соединен с землей, а источник напряжения подключен к неинвертирующему входу (справа). Для моделирования с обратной связью инвертирующий вход вместо земли будет подключен к узлу с надписью «feedback» (обратная связь). R₁ и R₂ образуют цепь обратной связи; эти резисторы расположены так, чтобы они напоминали типовой делитель напряжения, чтобы подчеркнуть тот факт, что коэффициент обратной связи β представляет собой часть (выраженную в виде дроби) от выходного сигнала, которая подается обратно и вычитается из входного сигнала. Показанные выше значения, т.е. R₁ = R₂ = 1 кОм, соответствуют β = (1 кОм) / (1 кОм + 1 кОм) = 0,5. Если мы уменьшим R₂ до 100 Ом, мы получим β = (100 Ом) / (100 Ом + 1 кОм) = 0,091.

Когда A равен Aβ

Сначала давайте взглянем на усиление без обратной связи (амплитуда – это сплошная кривая, фаза – это пунктирная кривая):

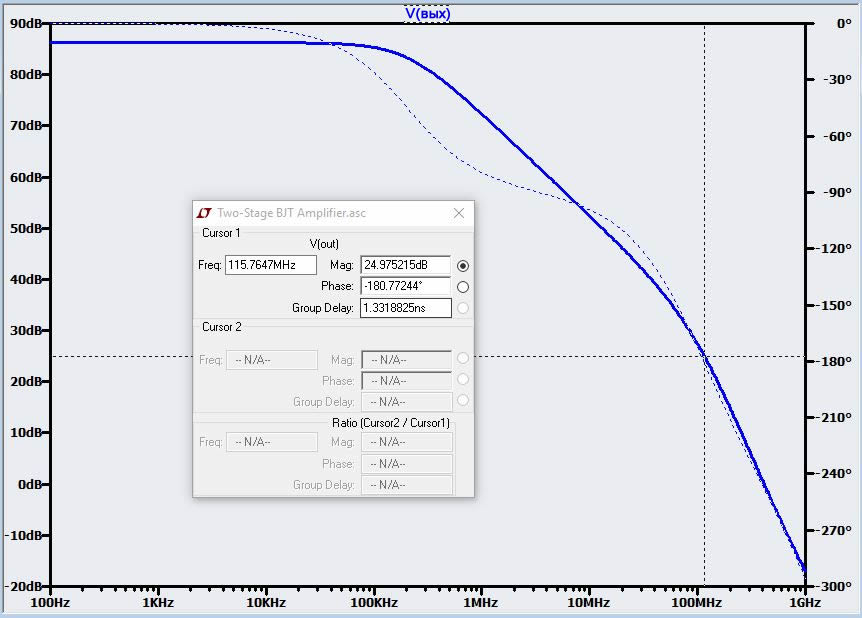
Первое, что нужно понять, это то, что это не только график частотной характеристики усилителя без обратной связи – это также график Aβ, когда β = 1. Напомним, что коэффициент усиления усилителя с обратной связью равен 1/β; таким образом, мы можем использовать частотную характеристику усилителя без обратной связи, чтобы определить, будет ли схема устойчивой, когда она настроена для коэффициента усиления с обратной связью, равного единице. Как видите, этот усилитель серьезно неустойчив: величина петлевого усиления при f₁₈₀ составляет 25 дБ. Поэтому мы определенно не будем использовать этот усилитель в качестве буфера с единичным усилением.

Выше усиление с обратной связью = ниже β = больше устойчивости

Теперь давайте посмотрим, как изменяется Aβ, когда β меньше 1. Мы сделаем это, подобрав значения R₁ и R₂ для требуемого коэффициента усиления обратной связью, а затем указав LTSpice построить график "V(вых)*(V(обр.связь)/V(вых))" (потому что β = V_{обр.связь}/V_вых). Обратите внимание, что схема у нас всё еще сконфигурирована для усиления без обратной связи (то есть инвертирующий вход соединен с землей). Мы моделируем коэффициент усиления A без обратной связи и затем строим график A, умноженный на β. Ниже показан график петлевого усиления для исходных значений резисторов R₁ = R₂ = 1 кОм (и, следовательно, β = 0,5):

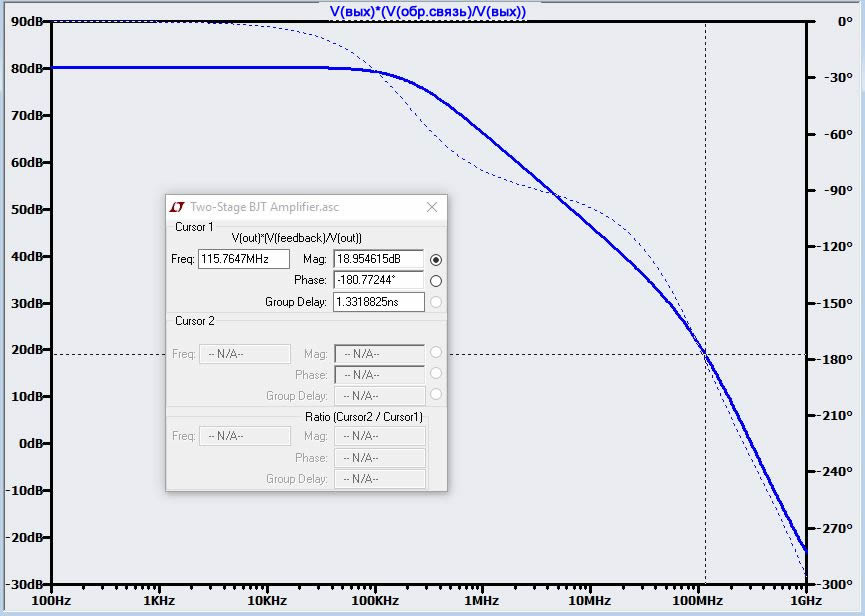
Теперь усиление на f₁₈₀ составляет 19 дБ вместо 25 дБ. Это улучшение, но мы всё еще далеки от устойчивости. Вы, возможно, заметили, что уменьшение величины петлевого усиления равно усилению с обратной связью, выраженному в децибеллах: G_ОС = 1/β = 2, а отношение по напряжению 2 = 6 дБ. Это имеет смысл, потому что, когда мы умножаем A на β, мы просто смещаем кривую A в соответствии со значением β в дБ (помните, что умножение на обычные числа переводится как сложение логарифмических значений). В этом примере β = 0,5 = -6 дБ, поэтому мы сдвигаем всю кривую А вниз на 6 дБ. (Эта простая связь справедлива только в том случае, если β постоянен по частоте, что, по сути, так и есть, когда цепь обратной связи состоит только из резисторов.)

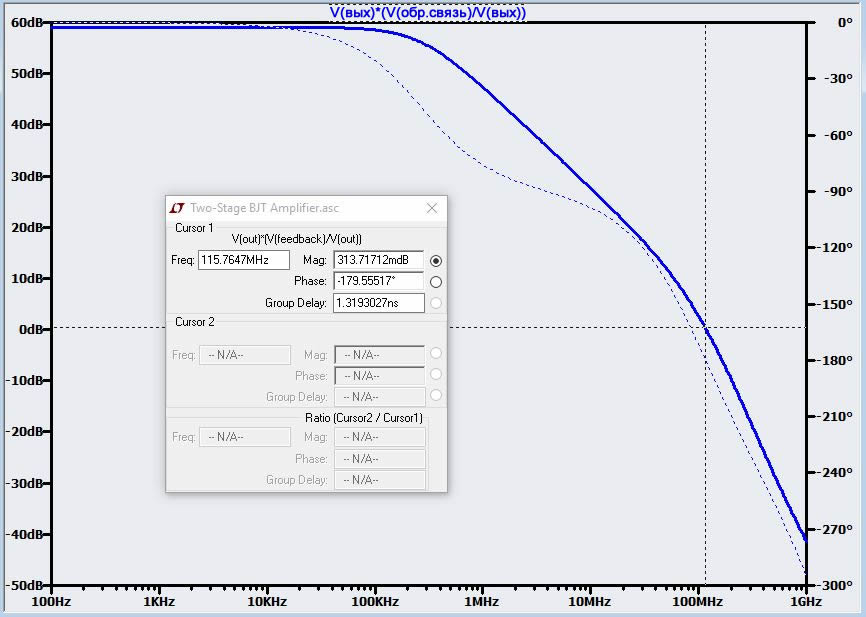
Теперь вы, вероятно, поняли, что нам не нужно слепо экспериментировать, чтобы определить усиление с обратной связью, при котором усилитель станет устойчивым. Мы можем легко увидеть, что, чтобы сместить график вниз достаточно далеко, чтобы получить при f₁₈₀ единичное петлевое усиление, необходимо усиление с обратной связью 25 дБ. Усиление 25 дБ соответствует отношению около 18 В/В, что означает β = 0,056. Мы можем получить это значение β с резисторами R₁ = 1 кОм и R₂ = 59 Ом:

Два параметра запаса

Теперь у нас есть единичное петлевое усиление при f₁₈₀. При небольшом увеличении коэффициента усиления с обратной связью мы получим граничную устойчивость усилителя. Какой коэффициент усиления с обратной связью нам нужен для достижения надежной устойчивости? Рассмотрим следующий график для G_ОС = 50 (и, следовательно, β = 0,02).

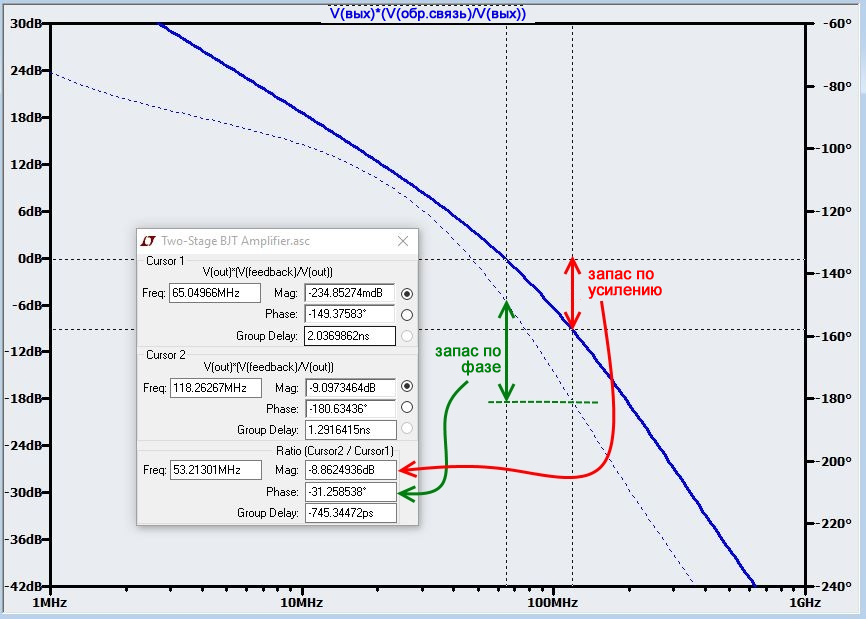
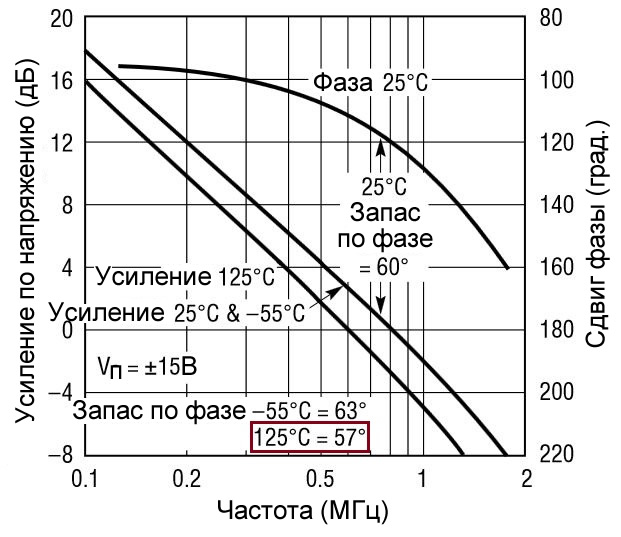
Первый курсор отмечает амплитуду, где она пересекает линию 0 дБ, а второй курсор отмечает амплитуду, где сдвиг фазы составляет 180°. Запас по усилению – это разница (выраженная в виде положительного значения в дБ) между 0 дБ и |Aβ| при f₁₈₀. Больший запас по усилению означает бо́льшую устойчивость. Аналогично, запас по фазе – это разница (выраженная как положительное число) между 180° и сдвигом фазы, где |Aβ| пересекает линию 0 дБ. Если это всё еще немного запутанно, посмотрите (вдумчиво) на приведенный выше график еще немного. Наиболее часто используемый показатель – это запас по фазе, возможно, потому, что у него есть удобное практическое правило: усилитель должен быть разработан так, чтобы запас по фазе был не менее 45°. Больший запас по фазе означает большую устойчивость, потому что более высокий запас по фазе указывает на то, что частота, на которой величина петлевого усиления достигает единицы, находится дальше от частоты страшного сдвига фазы на 180°, превращающего отрицательную обратную связь в положительную. Следующий график для операционного усилителя LT1001 от Linear Tech показывает, что коэффициент усиления без обратной связи рассчитан на минимальный запас по фазе 57°, что означает, что усилитель будет полностью стабильным, даже если β = 1.

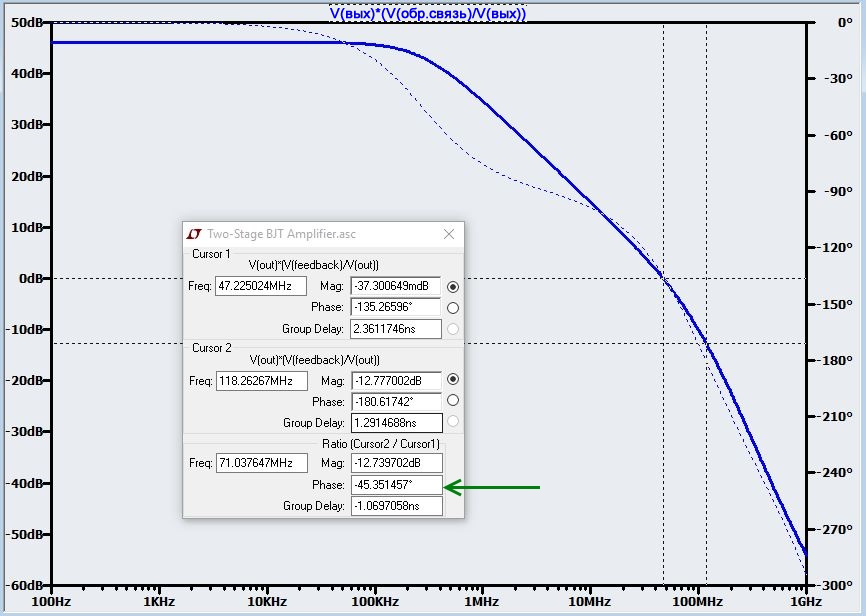
Наш усилитель для достижения запаса по фазе 45° должен быть настроен на коэффициент усиления с обратной связью около 78 (β = 0,013):

Заключение

Теперь мы знаем базовый подход для моделирования петлевого усиления, и мы исследовали взаимосвязь между β, коэффициентом усиления с обратной связью и устойчивостью. Мы также знаем, что запас по фазе может помочь нам решить, является ли усилитель достаточно устойчивым. В следующей статье мы подробно обсудим альтернативный (а в некоторых случаях весьма полезный) способ использования A и β для оценки устойчивости.

Теги