Отрицательная обратная связь, часть 7: частотно-зависимая обратная связь
Рассмотрим, почему частотная характеристика сети обратной связи может серьезно, а иногда и неожиданно ухудшить стабильность.
Вспомогательная информация
- Введение в операционные усилители
- Операционные усилители: отрицательная обратная связь
- Фаза сигнала переменного тока
- Введение в биполярные транзисторы
Чтобы вам не приходилось переключаться между страницами каждый раз, когда вы хотите обдумать общую структуру обратной связи, вот схема, представленная в первой статье:
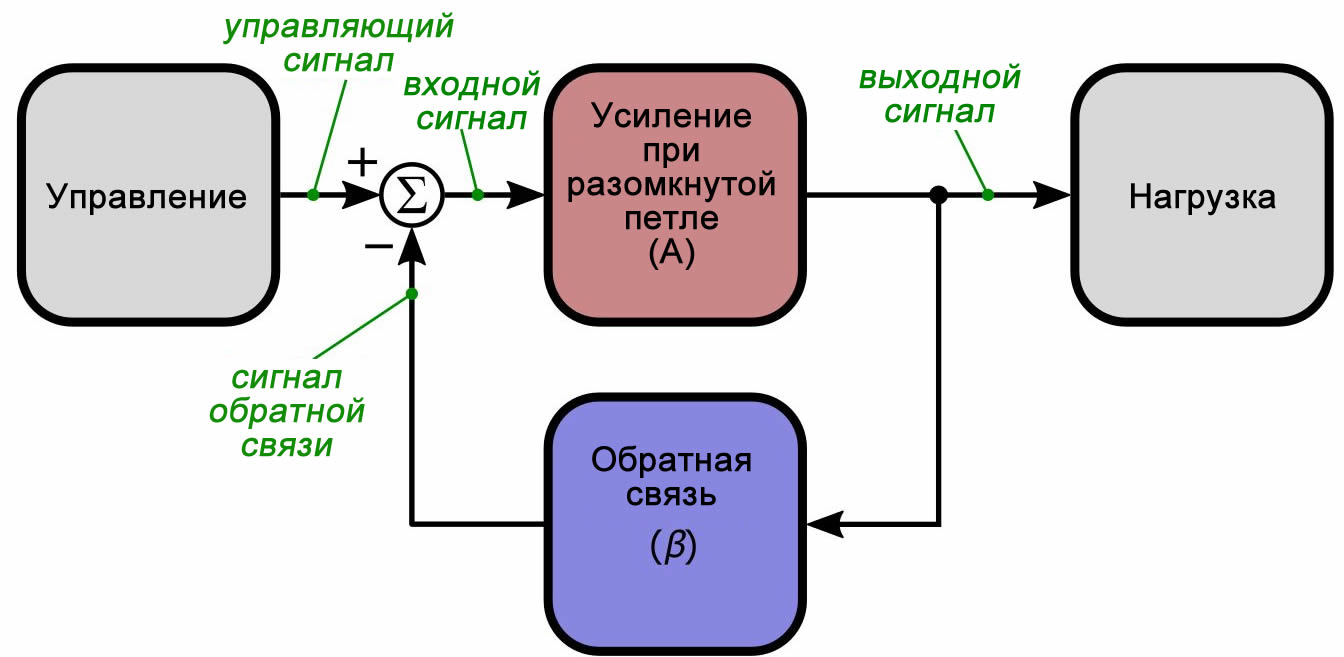
А вот схема усилителя для моделирования LTSpice, которую мы начали обсуждать в пятой части:
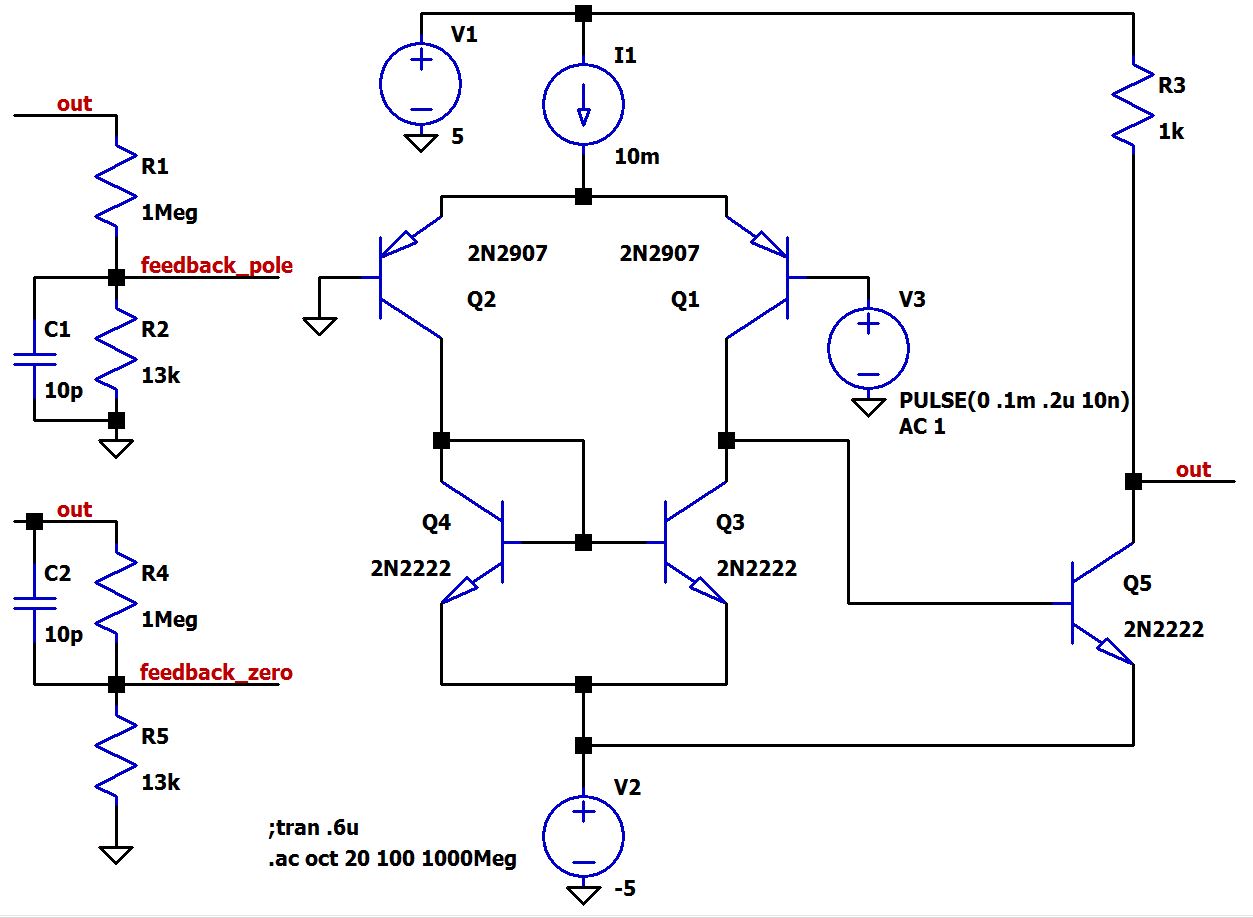
Обратите внимание, что теперь у нас есть две цепи обратной связи: в одной конденсатор добавлен параллельно нижнему резистору, а в другой конденсатор добавлен параллельно верхнему резистору.
Остерегайтесь полюсов и нулей
В предыдущих статьях мы фокусировались на схемах обратной связи, состоящих исключительно из резисторов. Прежде чем паразитные емкость и индуктивность резисторов окажут существенное влияние на схему, нам нужно подняться в гигагерцовый диапазон; поэтому для наших целей мы могли предположить, что цепь обратной связи только из резисторов не зависит от частоты проходящего через нее сигнала. Но теперь нам нужно посмотреть, что происходит, когда коэффициент обратной связи β изменяется в зависимости от частоты сигнала – иными словами, теперь и A, и β являются функциями от частоты, тогда как ранее A был передаточной функцией, а β был константой. Начнем с рассмотрения графика A-и-1/β для цепи обратной связи, состоящей из R1, R2 и C1.
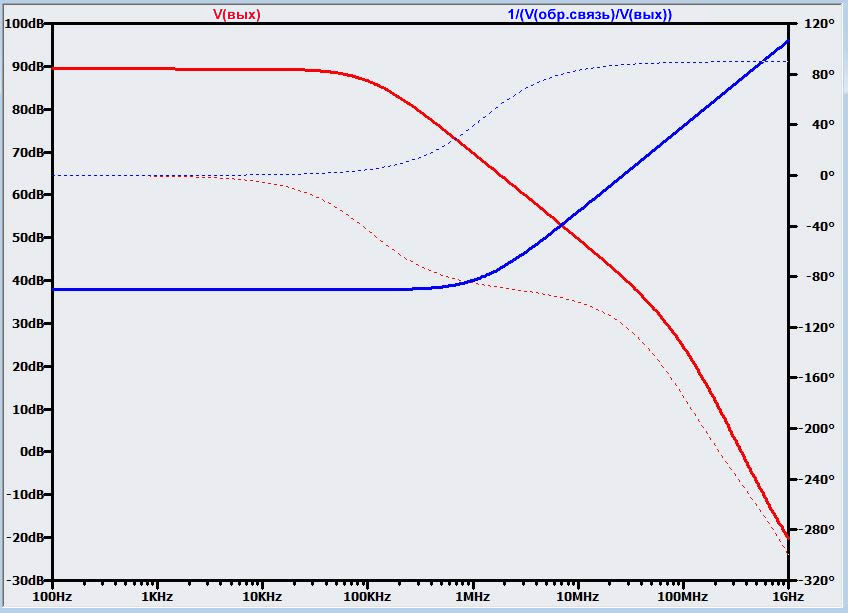
Как указано в легенде диаграммы, синяя линия – это кривая 20lg(1/β) для узла, отмеченного как «feedback_pole» (обратная связь, полюс). Эта метка неизбежно вводит в заблуждение – «полюс» подразумевает уменьшение амплитуды отклика, тогда как кривая демонстрирует увеличение амплитуды отклика. Но «полюс» относится к тому, что сама цепь обратной связи включает в себя полюс в передаточной функции, что означает, что величина β уменьшается по мере увеличения частоты выше частоты полюса. Кривая, показанная выше, демонстрирует противоположный отклик, потому что это график 20lg(1/β), а не 20lg(β). Аналогично, узел, отмеченный как «feedback_zero» (обратная связь, ноль), имеет ноль в передаточной функции обратной связи, что соответствует кривой 20lg (1/β) с уменьшением амплитуды отклика.
Итак, сначала давайте вспомним наш обобщенный метод точки пересечения для анализа устойчивости: если разница между наклоном амплитудно-частотной характеристики усилителя без обратной связи и наклоном амплитудно-частотной характеристики усилителя с обратной связью не превышает 20 дБ/декада в точке пересечения, усилитель достаточно устойчив. Используя это правило, мы можем легко увидеть, что наш усилитель уже недостаточно устойчив. Добавление конденсатора параллельно с нижним резистором обратной связи приводит к росту кривой 20lg(1/β) на 20 дБ/декада, начиная примерно с 1 МГц. Следовательно, в точке пересечения наклон 20lg(A) составляет -20 дБ/декада, а наклон 20lg(1/β) составляет +20 дБ/декада. Таким образом, разница между наклонами составляет +20 дБ/декада - (-20 дБ/декада) = 40 дБ/декада. Это нарушает обобщенный критерий точки пересечения, поэтому схема недостаточно устойчива.
Анализ альтернативного подхода
Этот пример удачно иллюстрирует преимущества и интуитивные аспекты этого альтернативного подхода к анализу устойчивости:
- Визуальная природа этих двух кривых делает необходимую информацию (т. е. является ли моя схема достаточно устойчивой) сразу явной. При необходимости подробную информацию о запасе по усилению или по фазе можно получить позже, построив график петлевого усиления.
- Отдельные кривые A и 1/β быстро дают полезную информацию о факторах, влияющих на устойчивость. В этом случае, очевидно, что виновником является амплитудно-частотная характеристика схемы с обратной связью. Особенно учитывая, что, продлив амплитудно-частотную характеристику схемы с обратной связью на низких частотах до кривой коэффициента усиления без обратной связи, мы можем подтвердить, что схема была бы достаточно устойчивой, если бы цепь обратной связи не зависела от частоты.
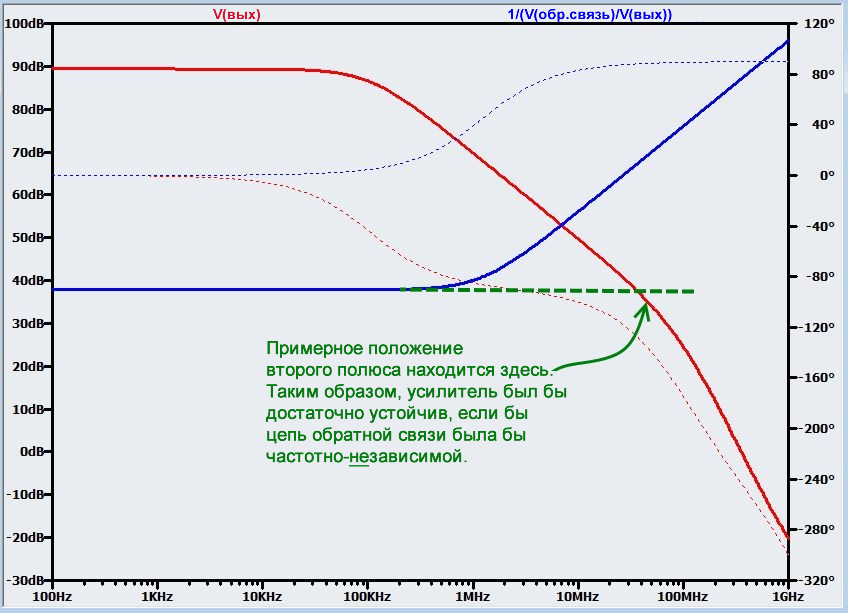
Рисунок 4 – Что было бы, если бы цепь обратной связи была частотно-независимой - Расстояние между полюсом обратной связи и кривой коэффициента усиления без обратной связи дает приблизительную, хотя и полезную информацию о том, насколько нам нужно подстроить амплитудно-частотную характеристику цепи обратной связи, чтобы сделать эту схему достаточно устойчивой, кривая 20lg(1/β) должна быть плоской (т.е. наклон = 0), когда она пересекает кривую 20lg(A).
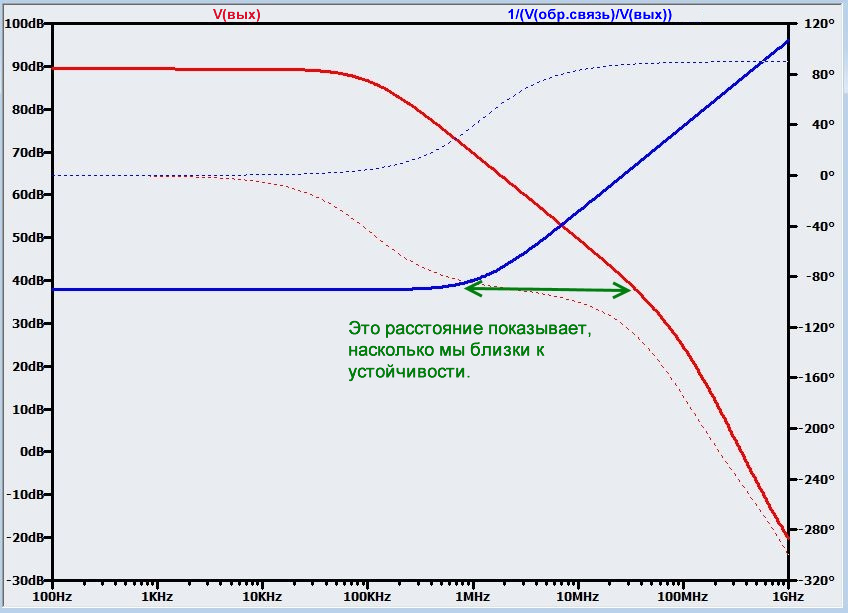
Рисунок 5 – Определение того, насколько схема усилителя далека от устойчивости - Этот метод проясняет, что частота полюса цепи обратной связи должна быть выше частоты пересечения, как показано на следующем графике, который включает в себя кривые для нескольких цепей обратной связи с различными значениями емкости. На этом графике также приведены соответствующие запасы по фазе (полученные с помощью стандартного анализа петлевого коэффициента усиления) для каждой кривой, чтобы дать вам представление о взаимосвязи между запасом по фазе и более наглядной информацией об устойчивости, передаваемой пересечением кривых 20lg(A) и 20lg(1/β).
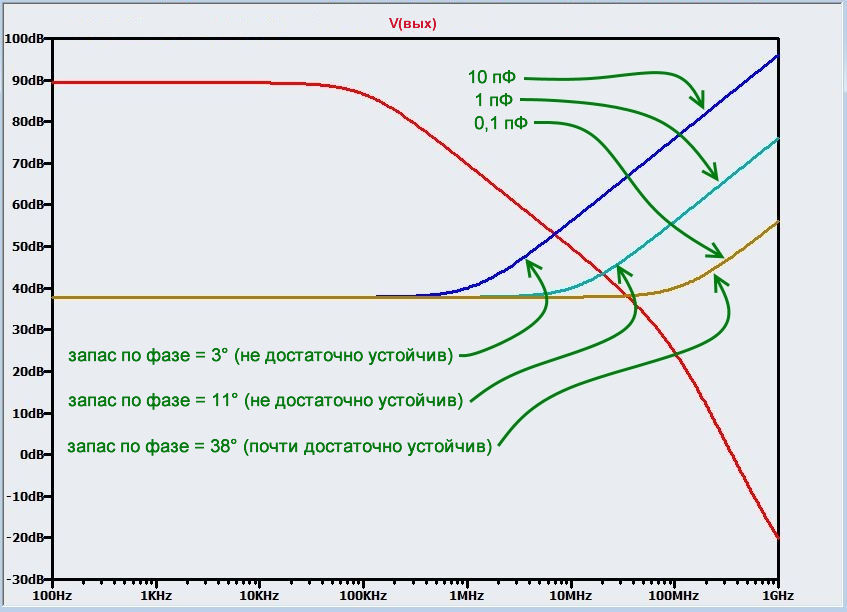
Рисунок 6 – Изменение устойчивости схемы в зависимости от частоты полюса цепи обратной связи (в данном случае, от значения емкости конденсатора) - Для этой схемы и других подобных ей график A и 1/β помогает нам визуализировать то, что в противном случае могло бы вызвать путаницу. В предыдущих статьях мы видели, что более высокий коэффициент усиления с обратной связью делает усилитель с отрицательной обратной связью более устойчивым. Но подождите! У нас есть полюс в цепи обратной связи, что приводит к коэффициенту усиления с обратной связью, который явно увеличивается с ростом частоты, но схема менее устойчива. В чем дело? Разница между наклонами примерно в 40 дБ/декада сразу же говорит нам о том, что у нас есть проблемы с устойчивостью. Кроме того, важность наклонов и расположения полюсов в этом аналитическом методе помогает нам помнить, что устойчивость в основном связана со сдвигом фазы, который вызывается полюсами (и нулями). Вот почему, когда β является функцией от частоты, более высокий коэффициент усиления с обратной связью может привести к неустойчивости: полюс в цепи обратной связи также вносит дополнительный сдвиг фазы, что приводит к большему суммарному сдвигу фазы в схеме с обратной связью, когда значение петлевого усиления достигает единицы.
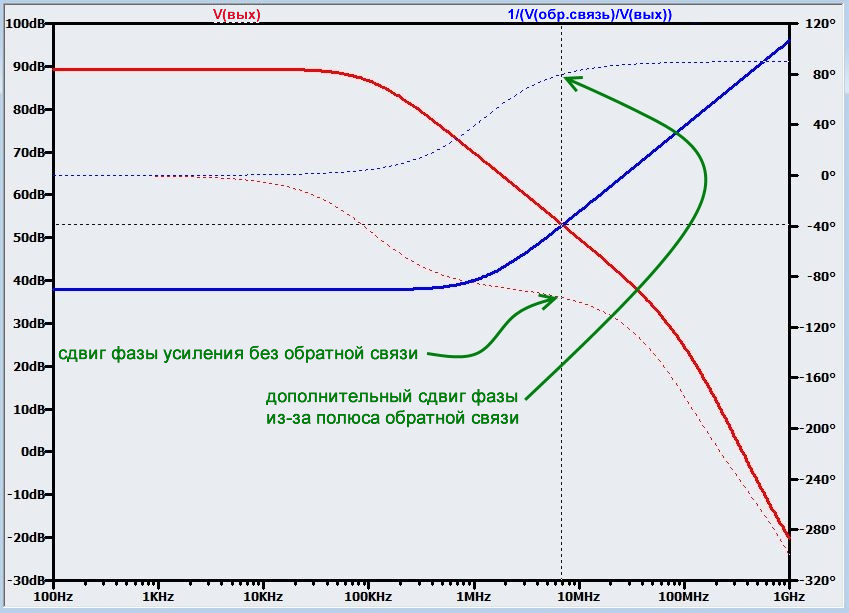
Рисунок 7 – Полюс в цепи обратной связи также вносит дополнительный сдвиг фазы
Нули тоже могут вызывать проблемы
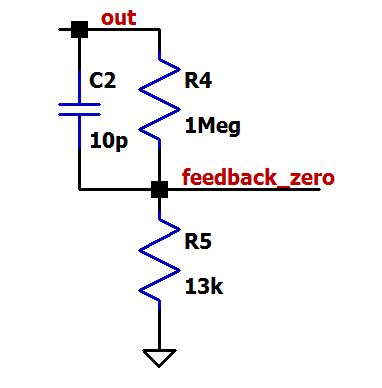
Вот график A и 1/β для схемы обратной связи, состоящей из R4, R5 и C2.
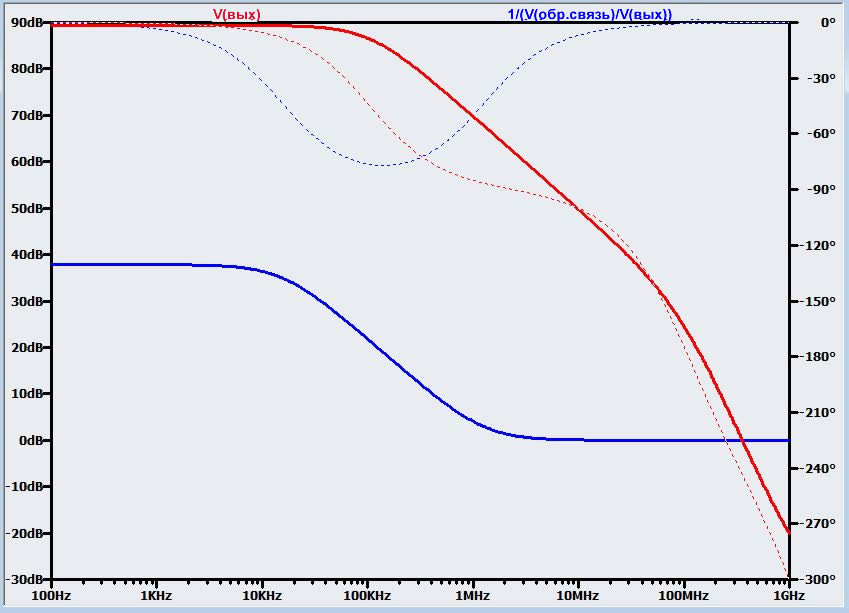
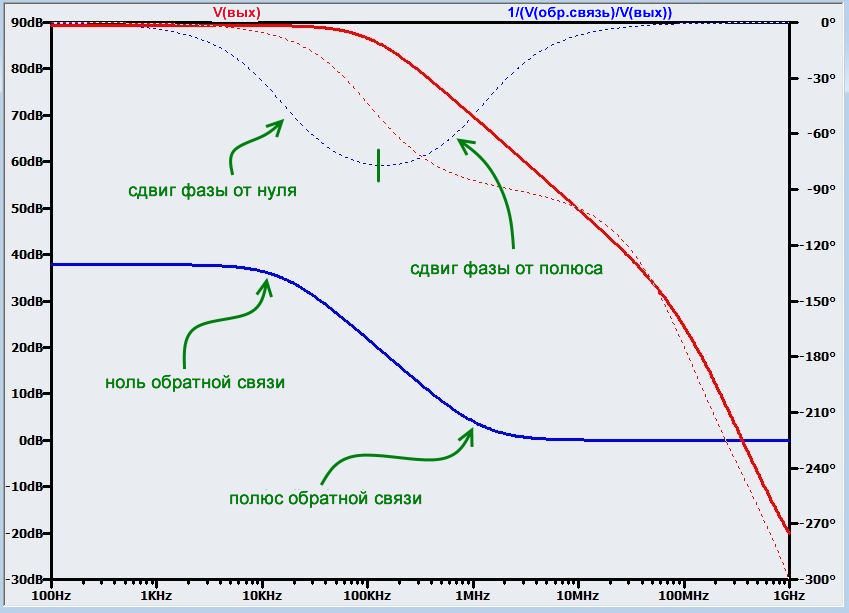
Как видите, емкость в цепи обратной связи может быть причиной проблем и там, и там. Благодаря полюсу, дополнительный сдвиг фазы лишил нас устойчивости. Теперь у нас есть ноль, которому удалось переместить точку пересечения на участок 40 дБ/декада на кривой 20lg(A). Проблема здесь в том, что у нас фактически есть и ноль, и полюс, результат, который вы можете понять, интуитивно оценивая схему обратной связи:
Как и ожидалось, величина β увеличивается по мере того, как полное сопротивление C2 уменьшается при увеличении частоты. Но затем кривая снова выравнивается, потому что, когда полное сопротивление C2 приближается к нулю, β приближается (и не превышает) к 1. (Простой анализ подтвердит, что передаточная функция имеет корень и в числителе, и в знаменателе.)
Сдвиг фазы, генерируемый нулем, должен помочь нам, учитывая, что его полярность противоположна полярности сдвига фазы, который мы видели у первой схемы цепи обратной связи. Но весь полезный фазовый сдвиг от нуля компенсируется сдвигом фазы от полюса, поэтому сдвиг фазы в цепи обратной связи почти равен нулю на частоте пересечения. Что нам остается, так это уменьшение коэффициента усиления с обратной связью, вызванное нулем, и с этим уменьшенным усилением с обратной связью кривая 20lg(1/β) пересекает кривую 20lg(A) на частоте, намного превышающей второй полюс в передаточной функции схемы без обратной связи.
Заключение
Мы видели, что частотно-зависимые элементы в цепи обратной связи могут вызывать все виды вреда тем, кто хочет усилитель, который усиливает, а не создает колебания. Кроме того, вы, возможно, заметили, что конденсаторы, использованные в представленных моделированиях, были довольно маленькими. Это правда, что их губительное влияние было усугублено неустойчивостью без обратной связи этого конкретного усилителя на дискретных биполярных транзисторах и большими резисторами, используемыми в цепи обратной связи; тем не менее, мы должны помнить, что небольшое количество дополнительной емкости (в некоторых случаях, возможно, даже паразитной емкости) может оказать нетривиальное влияние на устойчивость. В следующей статье мы будем использовать концепции, исследуемые здесь, чтобы исследовать устойчивость необычно склонной к колебаниям схемы: трансимпедансный усилитель усиления тока фотодиода.
