Введение в теорию обучения нейронных сетей
В данной статье мы рассмотрим обучение перцептрона с более теоретической точки зрения, сосредоточившись на «чаше ошибки».
Эта статья является частью серии статей по нейронным сетям. Если вы хотите наверстать упущенное, прежде чем двигаться вперед, то можете найти остальную часть серии выше, в меню с содержанием.
В данной статье мы рассмотрим теорию и практику обучения нейронных сетей и рассмотрим концепцию чаши ошибки.
Обучение: теория против практики
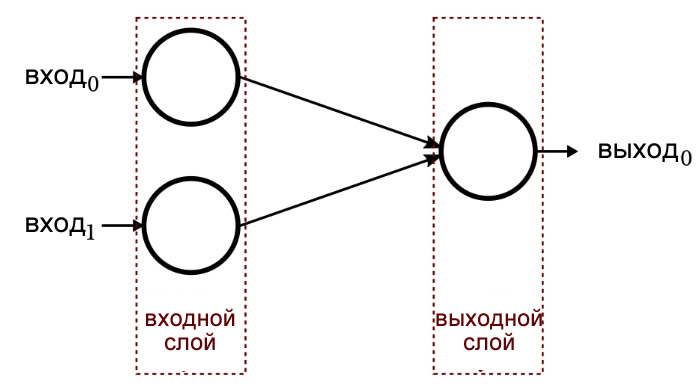
На первый взгляд, обучение нейронной сети кажется довольно простым. Когда мы работаем с простой сетью (такой как однослойный перцептрон, показанный ниже), математика, необходимая для обучения, конечно, не является непреодолимой, сама сеть может быть реализована в относительно короткой программе, написанной на распространенных языках, таких как C или Python, и процесс обучения не требует чрезмерного количества вычислительного времени.
Кроме того, общая концепция напоминает действие стабилизации, связанное с отрицательной обратной связью: мы применяем входные данные, производим выходные данные, сравниваем полученные выходные данные с ожидаемым выходным сигналом и передаем эту информацию обратно в нейросеть таким образом, чтобы веса могли постепенно сходиться на значениях, которые подходят для поставленной задачи.
Однако, как вы, вероятно, уже знаете, или уже догадались, существует довольно много теории, связанной с обучением искусственных нейронных сетей – выполните поиск «neural network training» в Google Scholar, и вы получите хорошую выборку исследований, которые были проведены в этой области.
К счастью, я не буду цитировать какие-либо научные публикации в этой статье. Наша цель на данный момент состоит в том, чтобы понять одну основополагающую концепцию, а именно, минимизацию ошибок.
Перцептрон как универсальный аппроксиматор
Нейронная сеть может выполнять классификацию, потому что она автоматически находит и реализует (посредством обучения) математические связи между входными данными и выходными значениями. В математической терминологии мы используем слово «функция», чтобы идентифицировать связь вход-выход, и мы часто выражаем функции в символах как f(x), например, f(x) = sin(x). Таким образом, x представляет входные данные, а f(x) устанавливается равной процедуре, которую мы используем, когда хотим, чтобы функция работала с входными данными и производила выходные значения.
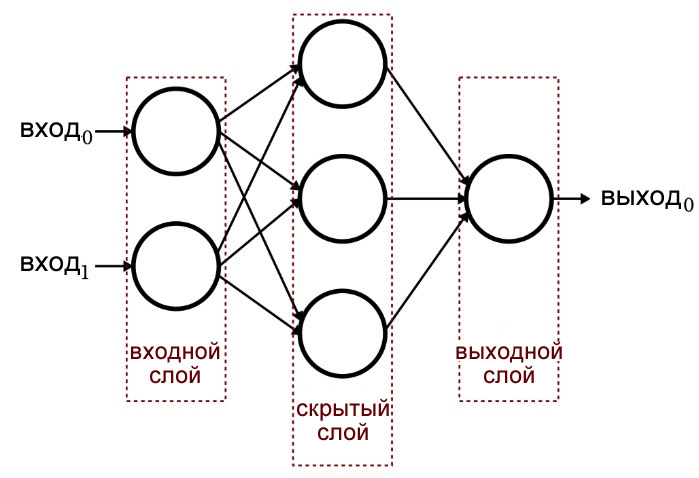
Перцептрон, который включает в себя дополнительный слой узлов (то есть, больше, чем просто входной и выходной слои), называется многослойным перцептроном, или MLP (multilayer perceptron). Эти узлы составляют скрытый слой, потому что они не «видны» непосредственно со стороны входа или выхода. Данная архитектура показана на диаграмме ниже и будет подробно рассмотрена в следующих статьях.
Многослойный перцептрон считается универсальным аппроксиматором. Существуют различные нюансы, связанные с этой концепцией, но общая идея заключается в том, что математика, выполняемая нейросетью, обеспечивает огромную гибкость в итоговой функции (я имею в виду функцию, как в f(x), т.е. связь между входом и выходом), т.е. созданными нейросетью математическими операциями.
Когда сеть впервые начинает обучение, весам были присвоены случайные значения, и, следовательно, f(x) нейросети (мы будем называть это fнс(x)) совсем не соответствовала реальной связи, fреал(x), между входом и выходом. Во время обучения нейросеть генерирует полезные корректировки значений веса, просматривая информацию об ошибках, возвращаемую из выходных данных, и fнс(x) постепенно становится всё более и более близкой к fреал(x), что-то вроде точного отражения, которое медленно проявляется в зеркале при испарении конденсата. (Примечание. В этом случае символ x не представляет одну переменную, как будто размерность входного слоя нейросети равна единице. Он представляет входные данные в общем виде. Например, x может быть вектором из 50 элементов.)
Чаша ошибки
Давайте предположим, что мы работаем с нейронной сетью, в которой есть два взвешенных соединения, ведущих к одному выходному узлу. Если мы обучаем нейросеть, мы знаем правильное выходное значение, и, следовательно, мы можем вычислить ошибку, создаваемую этим выходным узлом. Кроме того, мы можем визуализировать ошибку, используя трехмерный график: два входа соответствуют оси x и оси y, а ошибка соответствует оси z.
Основная идея здесь заключается в том, что каждая комбинация входных весов и выходной ошибки подобна точке в трехмерном пространстве. При изменении весов компоненты x и y точки изменяются, и компонент z также изменяется, если изменение веса приводит к изменению ошибки. Когда весовые коэффициенты улучшаются, ошибка уменьшается в сторону нуля, и это представлено трехмерной чашей ошибки, показанной ниже.
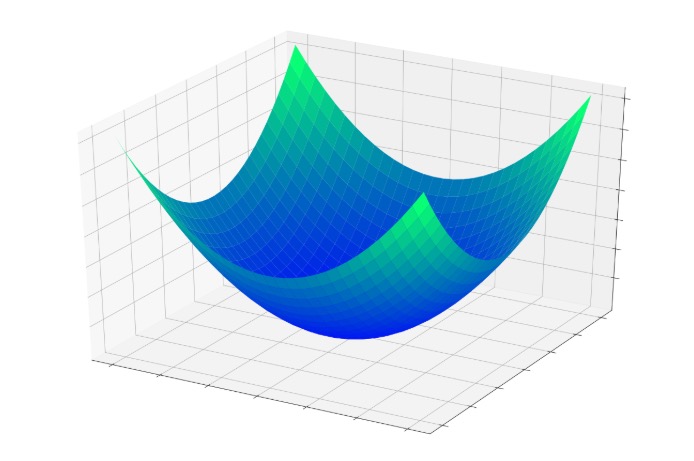
Процедура обучения – это, по сути, стремление к дну этой чаши, где z = 0, потому что, если z = 0, выходные данные, произведенные узлом, равны ожидаемым выходным данным. По мере того, как веса постепенно корректируются во время обучения, точка, определяемая двумя весами и ошибкой, движется вдоль поверхности этой чаши, вероятно, направляясь вниз.
Эта визуальная аналогия возвращает нас к понятию аппроксимации функции: спуск к минимальной ошибке происходит при изменении весов, и изменения весов также делают fнс(x) постепенно похожей на fреал(x). Подводя итог, можно сказать, что обучение заставляет нейросеть изменять свои веса таким образом, чтобы это приводило к минимизации функции ошибки и приводило к тому, что математические операции всей нейросети приближались к математической связи между входом и выходом.
Заключение
Я надеюсь, что эта статья дала вам более глубокое понимание обучения нейронной сети. В следующей статье мы продолжим эту тему с обсуждением скорости обучения.
