Понятие скорости обучения в нейронных сетях
В данной статье обсуждается скорость обучения, которая играет важную роль в обучении нейронной сети.
Добро пожаловать в серию статей по основам нейронных сетей. Чтобы узнать о нейронных сетях перцептрон и теории обучения нейронных сетей в целом, ознакомьтесь с содержанием серии выше, в меню над статьей.
В этой статье мы обсудим концепцию скорости обучения и выясним, как она может повлиять на обучение нейронной сети.
Что такое скорость обучения?
Как вы уже догадались, скорость обучения влияет на скорость, с которой обучается ваша нейронная сеть. Но это еще не всё.
Во-первых, давайте проясним, что мы подразумеваем под «обучением». В контексте нейронных сетей «учиться» по значению более или менее эквивалентно «тренироваться», но с другой стороны это разные вещи. Инженер обучает нейронную сеть, предоставляя обучающие данные и выполняя процедуру обучения. В то время как это происходит, сеть учится – или, более конкретно, она учится аппроксимировать связь вход-выход, содержащуюся в обучающих данных. Проявлением обучения является изменение веса, а скорость обучения влияет на способ этого изменения.
Минимизация ошибок в нейронных сетях
В предыдущей статье была представлена концепция чаши ошибки, то есть трехмерной поверхности, которая помогает нам визуализировать процесс, посредством которого ошибка узла постепенно уменьшается до нуля по мере того, как его входные весовые коэффициенты изменяются во время обучения.
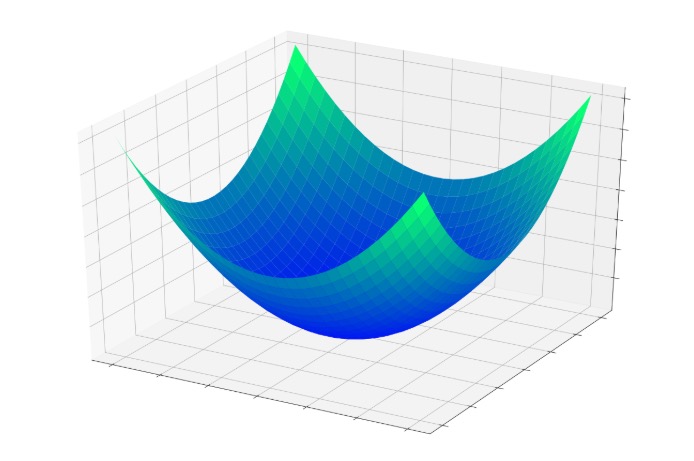
Если у нас есть точка, местоположение которой определяется значениями двух весов и выходной ошибкой узла, каждая модификация весов заставляет точку перескакивать в другое место где-нибудь на этой поверхности ошибки. Эти прыжки стремятся к нижней части чаши, где ошибка сводится к минимуму; они не приводят напрямую к минимальной ошибке, потому что каждая обучающая выборка – это только маленький кусочек математической головоломки.
Влияние скорости обучения
Скорость обучения влияет на размер прыжков, которые ведут к нижней части чаши. Сейчас я собираюсь перейти к двумерному представлению, потому что будет легче создавать и интерпретировать изображения. Вот наша двумерная функция ошибки:
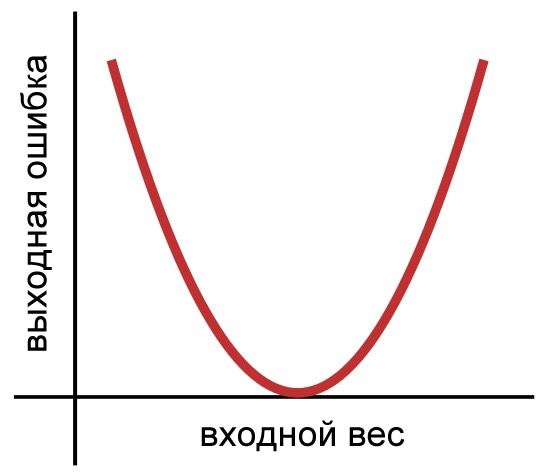
Как вы помните из предыдущей статьи, для обновления весов мы использовали следующее правило обучения:
\[w_{новый} = w+(\alpha\times\delta\times вход)\]
где \(\alpha\) – это скорость обучения, а \(\delta\) – это разница между ожидаемым выходным сигналом и рассчитанным выходным сигналом (то есть ошибка).
Каждый раз, когда мы применяем это правило обучения, вес переходит в новую точку на кривой ошибки. Если \(\delta\) велика, эти скачки также могут быть довольно большими, и нейросеть может обучаться неэффективно, потому что веса не сходятся постепенно к минимальной ошибке. Вместо этого они хаотично прыгают, как показано ниже.
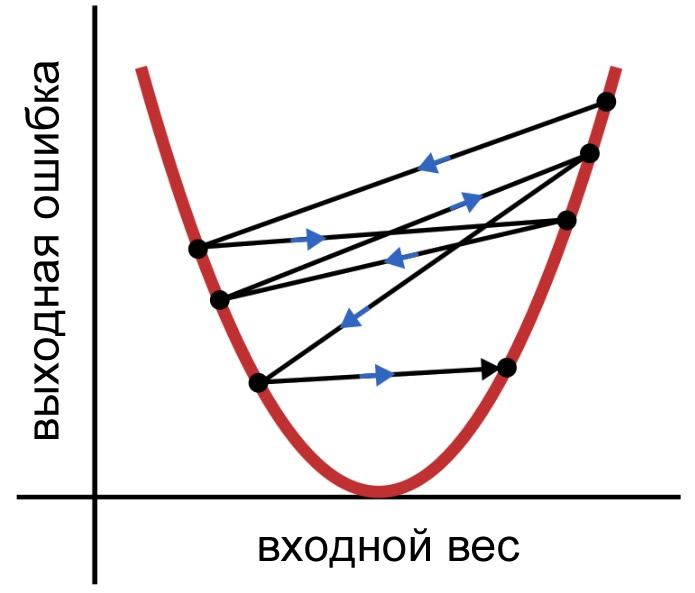
Так как, прежде чем модификация применяется к весу, \(\delta\) умножается на скорость обучения, мы можем уменьшить размер прыжков, выбрав \(\alpha\) <1. Цель – использовать скорость обучения для обеспечения умеренно быстрой и последовательной сходимости.
Тип обучения, который нам нужен, может выглядеть примерно так:
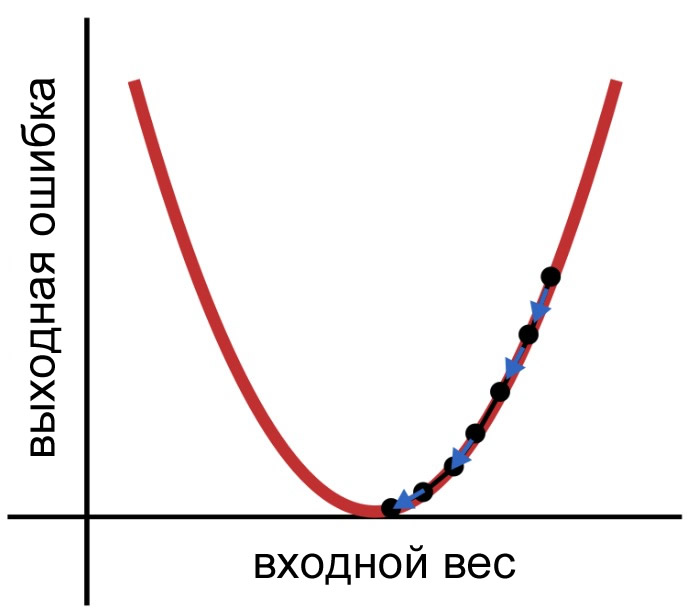
Как выбрать скорость обучения
Не существует универсального правила, которое говорит вам, как выбрать скорость обучения, и нет даже точного и аккуратного способа определить оптимальную скорость обучения для заданного приложения. Обучение – это сложный и изменчивый процесс, и когда дело доходит до скорости обучения, вы должны полагаться на интуицию и эксперименты.
Если ваша нейросеть может быстро обрабатывать обучающие данные, вы можете просто выбрать несколько разных скоростей обучения и сравнить полученные веса (если вы знаете, какими они должны быть) или ввести свежие данные и оценить взаимосвязь между скоростью обучения и точностью классификации.
Более сложный подход, который был бы более практичным для нейросетей, требующих длительного времени обучения, заключается в анализе изменений в ошибках во время обучения сети. Ошибка должна уменьшаться в направлении минимума, а изменения в ошибке должны быть достаточно малыми, чтобы избежать «прыгающего» поведения, показанного выше, но не настолько маленькими, чтобы нейросеть обучалась крайне медленно. Как и многие другие вещи в жизни, скорость обучения зависит от баланса.
О том, как найти оптимальную скорость обучения, можно сказать гораздо больше, и, возможно, мы рассмотрим этот вопрос более подробно в следующей статье. Но не сегодня.
График скорости обучения
Прежде чем мы закончим, я хочу кратко обсудить технику обучения, которая, я считаю, является важным инструментом для тех, кто работает с нейронными сетями. Первое, что нужно признать, это то, что скорость обучения не обязательно должна быть постоянной на протяжении всей процедуры обучения. Скорость обучения используется каждый раз, когда с помощью правила обучения обновляются веса; таким образом, если скорость обучения изменяется во время обучения, то тут же будет изменен и эволюционный путь нейросети к ее окончательной форме.
Одним из способов воспользоваться этим является снижение скорости обучения во время обучения. Это называется «отжигом» (annealing) скорости обучения. Есть разные способы реализовать это, но сейчас важно понять, почему это помогает.
Когда нейросеть начинает обучение, ошибка, вероятно, будет большой. Более высокая скорость обучения помогает нейросети делать большие шаги в направлении минимальной ошибки. Однако когда сеть приближается к нижней части кривой ошибки, эти длинные шаги могут препятствовать сходимости, подобно тому, как человеку, делающему длинные шаги, может быть трудно попасть прямо в середину небольшого круга, нарисованного на полу. Когда скорость обучения уменьшается, длинные шаги становятся меньшими шагами, и, в конце концов, нейросеть приближается к центру круга.
Заключение
Я предупреждал вас в первой статье, что это будет длинная серия. Это уже шестая статья, а конца еще не видно. В любом случае, я надеюсь, что вам понравилось это объяснение скорости обучения. В следующей статье мы обсудим проблему «локальных минимумов».
