Обучающие наборы данных для нейронных сетей: как обучить и проверить нейросеть на Python
В данной статье мы будем использовать для обучения многослойного перцептрона сгенерированные в Excel выборки, а затем посмотрим, как нейросеть работает с проверочными выборками.
Если вы хотите разработать нейронную сеть на Python, вы находитесь в правильном месте. Прежде чем углубиться в обсуждение о том, как использовать Excel для создания обучающих данных для вашей нейросети, для получения дополнительной информации посмотрите остальные статьи серии выше, в меню с содержанием.
Что такое обучающие данные?
В реальной жизни обучающие выборки состоят из данных измерений в сочетании с «решениями», которые помогут нейронной сети обобщить всю эту информацию в соответствующую связь вход-выход.
Например, предположим, что вы хотите, чтобы ваша нейронная сеть предсказывала вкусовые качества помидора на основе цвета, формы и плотности. Вы не представляете, как именно цвет, форма и плотность связаны с вкусностью, но вы можете измерить цвет, форму и плотность, и у вас есть вкусовые рецепторы. Таким образом, всё, что вам нужно сделать, это собрать тысячи и тысячи помидоров, записать их физические характеристики, попробовать каждый (лучшая часть), а затем поместить всю эту информацию в таблицу.
Каждая строка – это то, что я называю одной обучающей выборкой, и в ней четыре столбца: три из них (цвет, форма и плотность) являются столбцами входных данных, а четвертый – целевым выходным значением.
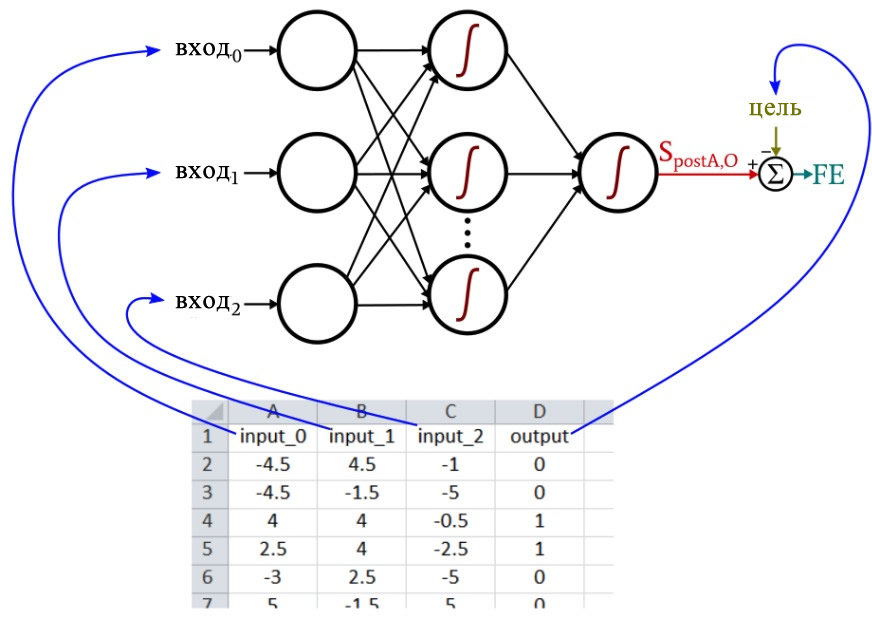
Во время обучения нейронная сеть найдет связь (если когерентная связь существует) между тремя входными значениями и выходным значением.
Оценка обучающих данных
Имейте в виду, что всё должно обрабатываться в числовом виде. Вы не можете в качестве входного параметра вашей нейронной сети использовать строку «сливовидная форма», а «аппетитный» не будет работать в качестве выходного значения. Вы должны количественно оценить ваши измерения и ваши классификации.
Для формы вы можете присвоить каждому помидору значение от –1 до +1, где –1 представляет собой идеальную сферу, а +1 означает крайне вытянутую форму. Что касается вкусовых качеств, вы можете оценивать каждый помидор по пятибалльной шкале от «несъедобного» до «восхитительного», а затем использовать унитарный код для сопоставления этих оценок с выходным вектором из пяти элементов.
Следующая диаграмма показывает, как этот тип кодирования используется для классификации выходных значений нейронной сети.
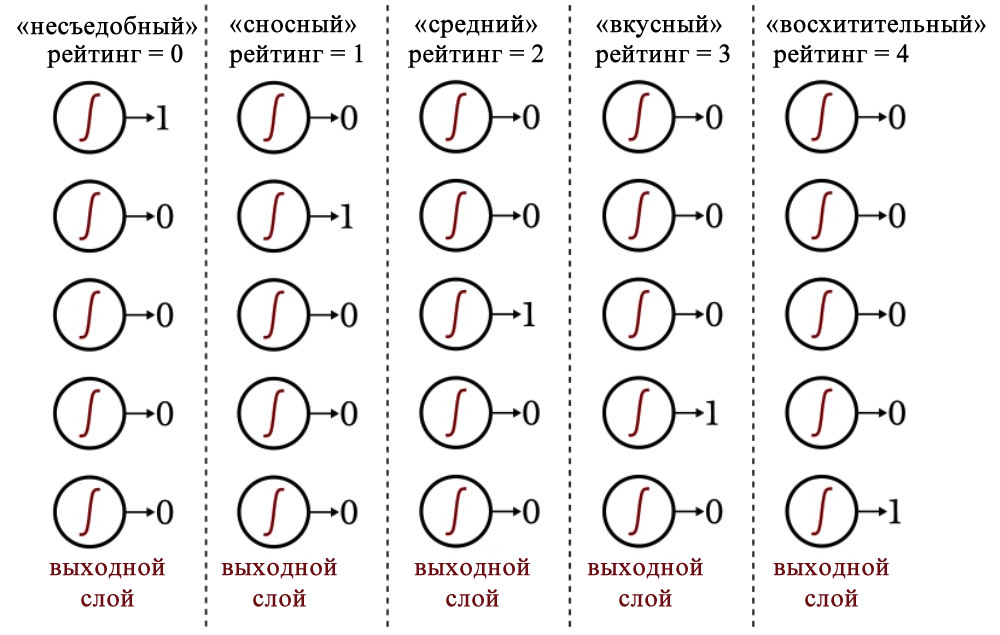
Выходная схема, использующая унитарный код, позволяет нам определить недвоичные классификации таким образом, чтобы это было совместимо с логистической сигмоидной функцией активации. Выходные данные логистической функции являются, по сути, двоичными, поскольку область перехода на графике является узкой по сравнению с бесконечным диапазоном входных значений, для которых выходное значение очень близко к минимальному или максимальному значению:
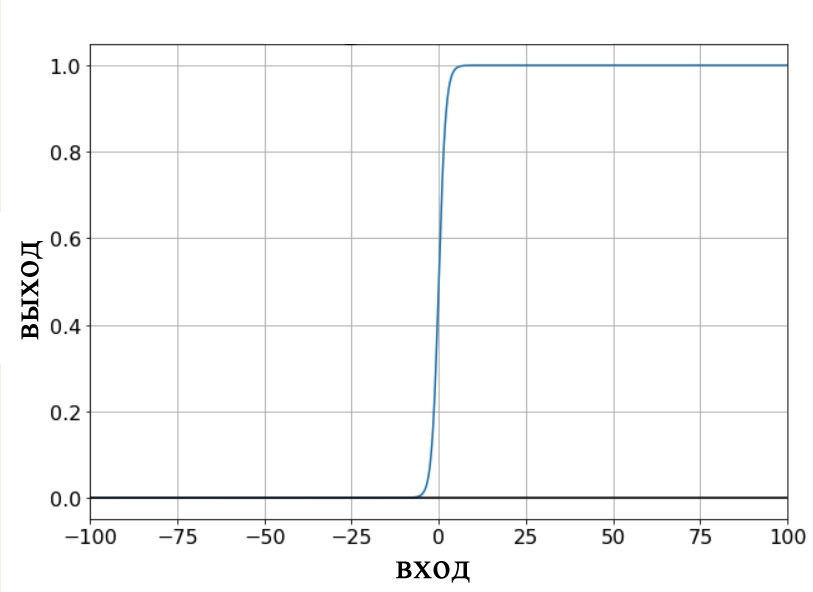
Таким образом, мы не хотим создавать эту нейросеть с одним выходным узлом, а затем предоставлять обучающие выборки, которые имеют выходные значения 0, 1, 2, 3 или 4 (или, если вы хотите оставаться в диапазоне от 0 до 1, это будут 0, 0,2, 0,4, 0,6 или 0,8), поскольку логистическая функция активации выходного узла будет устойчиво придерживаться минимального и максимального выходных значений.
Нейронная сеть просто не понимает, насколько нелепым было бы сделать вывод, что все помидоры либо несъедобны, либо восхитительны.
Создание набора обучающих данных
Нейронная сеть на Python, о которой мы говорили в части 12, импортирует обучающие выборки из файла Excel. Обучающие данные, которые я буду использовать для этого примера, организованы следующим образом:
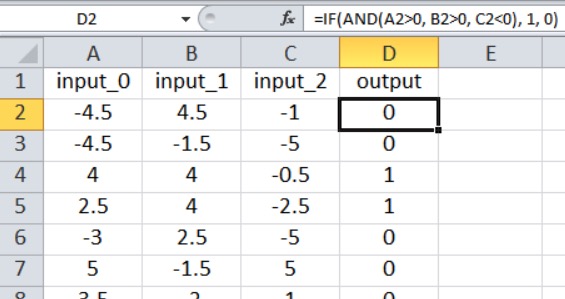
Наш текущий код для перцептрона ограничен одним выходным узлом, поэтому всё, что мы можем сделать, – это выполнить классификацию типа «истина/ложь». Входные значения – это случайные числа от –5 до +5, сгенерированные по формуле Excel:
=RANDBETWEEN(-10, 10)/2
Как показано на скриншоте, результат рассчитывается следующим образом:
=IF(AND(A2>0, B2>0, C2<0), 1, 0)
Таким образом, выходное значение равно true, только если input_0 больше нуля, input_1 больше нуля, а input_2 меньше нуля. В противном случае выходное значение равно false.
Это математическая связь вход-выход, которую перцептрон должен извлечь из обучающих данных. Вы можете создать столько выборок, сколько захотите. Для такой простой задачи, как эта, вы можете достичь очень высокой точности классификации с 5000 выборками и одной эпохой.
Обучение нейросети
Вам нужно установить входную размерность на три (I_dim = 3, если вы используете мои имена переменных). Я настроил нейросеть так, чтобы в ней было четыре скрытых узла (H_dim = 4), и выбрал скорость обучения 0,1 (LR = 0,1).
Найдите инструкцию training_data = pandas.read_excel(...) и введите название своей таблицы (если у вас нет доступа к Excel, библиотека Pandas также может читать файлы ODS). Затем просто нажмите кнопку «Run». Обучение с 5000 выборками занимает всего несколько секунд на моем ноутбуке.
Если вы используете полную программу «MLP_v1.py», которую я включил в часть 12, валидация(смотрите следующий раздел) начинается сразу после завершения обучения, поэтому перед тем, как приступить к обучению нейросети, вам необходимо подготовить данные валидации.
Валидация нейросети
Чтобы проверить эффективность нейросети, я создаю вторую электронную таблицу и генерирую входные и выходные значения, используя точно такие же формулы, а затем импортирую эти проверочные данные так же, как импортировал обучающие данные:
training_data = pandas.read_excel('MLP_Tdata.xlsx')
target_output = training_data.output
training_data = training_data.drop(['output'], axis=1)
training_data = np.asarray(training_data)
training_count = len(training_data[:,0])
validation_data = pandas.read_excel('MLP_Vdata.xlsx')
validation_output = validation_data.output
validation_data = validation_data.drop(['output'], axis=1)
validation_data = np.asarray(validation_data)
validation_count = len(validation_data[:,0])
В следующем фрагменте кода показано, как выполнить базовую валидацию:
#####################
# проверка
#####################
correct_classification_count = 0
for sample in range(validation_count):
for node in range(H_dim):
preActivation_H[node] = np.dot(validation_data[sample,:], weights_ItoH[:, node])
postActivation_H[node] = logistic(preActivation_H[node])
preActivation_O = np.dot(postActivation_H, weights_HtoO)
postActivation_O = logistic(preActivation_O)
if postActivation_O > 0.5:
output = 1
else:
output = 0
if output == validation_output[sample]:
correct_classification_count += 1
print('Percentage of correct classifications:')
print(correct_classification_count*100/validation_count)
Я использую стандартную процедуру прямого распространения для вычисления сигнала постактивации выходного узла, а затем использую оператор if/else для применения порогового значения, который преобразует значение постактивации в классификационное значение true/false.
Точность классификации вычисляется путем сравнения значения классификации с целевым значением для текущей выборки валидации, подсчета количества правильных классификаций и деления на количество выборок валидации.
Помните, что если вы закомментировали инструкцию np.random.seed(1), при каждом запуске программы веса будут инициализироваться различными случайными значениями, и, следовательно, точность классификации будет меняться от одного запуска к следующему. Я выполнил 15 отдельных запусков с параметрами, указанными выше, 5000 обучающих выборок и 1000 проверочных выборок.
Самая низкая точность классификации составила 88,5%, самая высокая – 98,1%, а средняя – 94,4%.
Заключение
Мы рассмотрели важную теоретическую информацию, относящуюся к обучающим данным нейронной сети, и провели первый эксперимент по обучению и валидации нашего многослойного перцептрона на языке Python. Я надеюсь, вам интересна эта серия статей о нейронных сетях – мы добились большого прогресса со времени первой статьи, и есть еще много, что нам нужно обсудить!
