Архитектура нейросети для реализации на Python

В данной статье обсуждается конфигурация перцептрона, которую мы будем использовать в наших экспериментах по обучению нейронных сетей и классификации, а также мы рассмотрим связанную с этим тему узлов смещения.

Добро пожаловать в серию технических статей о нейронных сетях. До сих пор в этой серии мы рассмотрели немало теории о нейронных сетях. Теперь мы готовы начать преобразование этих теоретических знаний в рабочую систему классификации на перцептроне.

Сначала я хочу представить общие характеристики сети, которые мы будем реализовывать на высокоуровневом языке программирования; я использую Python, но код будет написан так, чтобы облегчить перевод на другие языки, такие как C. В следующей статье будет приведен подробный разбор кода на Python, а после этого мы рассмотрим различные способы обучения, использования и оценки работы этой нейросети.

Архитектура нейронной сети на Python

Программное обеспечение соответствует перцептрону, изображенному на следующей диаграмме.

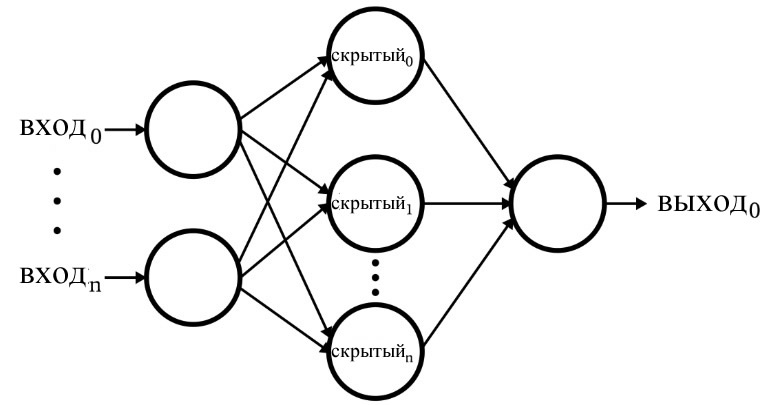
Основные характеристики нейросети:

• Количество входных узлов является переменным значением. Это важно, если мы хотим, чтобы сеть обладала значительной степенью гибкости, потому что размерность входных данных должна соответствовать размерности выборок, которые мы хотим классифицировать.
• Код не поддерживает несколько скрытых слоев. На данный момент в этом нет необходимости – для обеспечения крайне мощной классификации достаточно одного скрытого слоя.
• Количество узлов в одном скрытом слое является переменным значением. Нахождение оптимального количества скрытых узлов требует некоторых проб и ошибок, хотя есть рекомендации, которые могут помочь нам выбрать разумную отправную точку. Мы рассмотрим проблему размерности скрытого слоя в следующей статье.
• Количество выходных узлов в настоящее время зафиксировано на значении единица. Это ограничение сделает нашу первую программу немного проще, и мы можем включить переменную размерность выхода в улучшенную версию.
• Функция активации для скрытых и выходных узлов будет стандартной логистической сигмоидной связью:
  \[f(x)=\frac{1}{1+e^{-x}}\]

Что такое узел смещения? (aka cмещение – это хорошо, если вы перцептрон)

Пока мы обсуждаем архитектуру нейросети, я должен отметить, что нейронные сети часто включают в себя то, что называется узлом смещения (или вы можете называть это просто «смещением» без «узла»). Числовое значение, связанное с узлом смещения, является константой, выбранной разработчиком. Например:

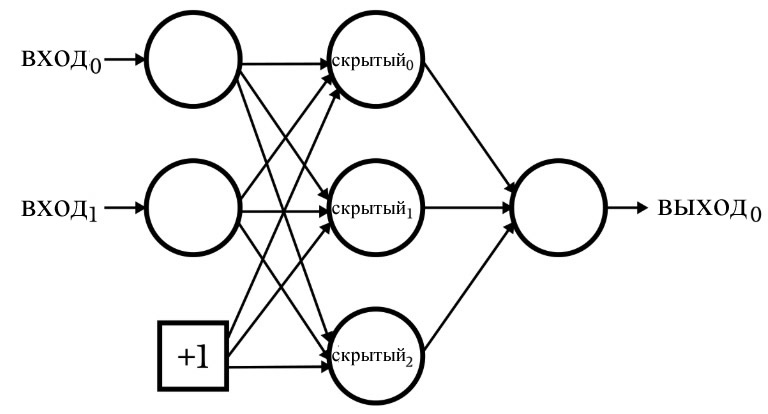
Узлы смещения могут быть включены во входной слой или в скрытый слой, или в оба. Их веса аналогичны любым другим весам и обновляются с использованием той же процедуры обратного распространения.

Использование узлов смещения является важным аспектом написания кода нейронной сети, который позволяет легко изменять количество входных или скрытых узлов – даже если вас интересует только одна конкретная задача классификации, переменная размерность входного и скрытого слоев гарантирует, что с помощью узлов смещения вы сможете удобно экспериментировать.

В десятой статье я указал, что сигнал преактивации узла вычисляется путем выполнения скалярного произведения, то есть вы поэлементно умножаете два массива (или вектора, если хотите), а затем суммируете эти произведения. Первый массив содержит значения постактивации из предыдущего слоя, а второй массив содержит веса, которые соединяют предыдущий слой с текущим слоем. Таким образом, если массив постактивации предыдущего слоя обозначен как x, а вектор весов обозначен как w, значение преактивации вычисляется следующим образом:

\[S_{preA} = w \cdot x = \sum(w_1x_1 + w_2x_2 + \cdots + w_nx_n)\]

Вы можете быть удивлены, что это имеет какое-то отношение к узлам смещения. Смещение (обозначается как b) изменяет эту процедуру следующим образом:

\[S_{preA} =( w \cdot x)+b = \sum(w_1x_1 + w_2x_2 + \cdots + w_nx_n)+b\]

Смещение сдвигает сигнал, который обрабатывается функцией активации, что может сделать сеть более гибкой и устойчивой. Использование буквы b для обозначения значения смещения напоминает «пересечение оси y» в стандартном уравнении для прямой линии: y = mx + b. И это не случайное совпадение. Смещение действительно похоже на «пересечение оси y», и вы также могли заметить, что массив весов эквивалентен наклону:

\[S_{preA} =( w \cdot x)+b\]

\[y = mx + b\]

Веса, смещение и активация

Если мы поразмыслим о числовых значениях, передаваемых функции активации узла во время обучения, то поймем, что веса увеличивают или уменьшают наклон входных данных, а смещение сдвигает входные данные по вертикали. Но как это влияет на выходное значение узла? Что ж, давайте предположим, что для активации мы используем стандартную логистическую функцию:

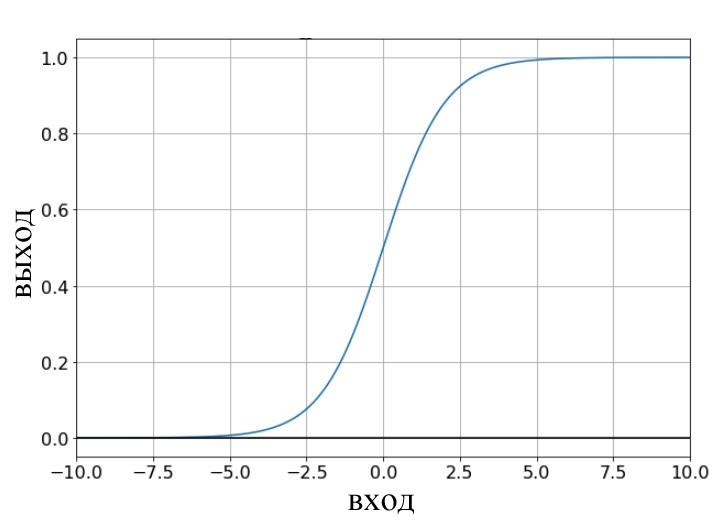
Переход от f_A(x) = 0 к f_A(x) = 1 отцентрирован при входном значении x = 0. Таким образом, используя смещение для увеличения или уменьшения сигнала преактивации, мы можем влиять на появление перехода и тем самым сдвигать график функции активации влево или вправо. Веса же определяют, как «быстро» входное значение проходит через x = 0, что влияет на крутизну перехода на графике функции активации.

Заключение

Мы обсудили узлы смещения и основные характеристики первой нейронной сети, которую мы реализуем программно обеспечение. Теперь мы готовы посмотреть на реальный код, что мы и сделаем в следующей статье

Теги