Как обучить простую нейронную сеть перцептрон
В данной статье представлен код на Python, который позволяет автоматически генерировать веса для простой нейронной сети.
Добро пожаловать в серию статей по нейронным сетям перцептрон. Если вы хотите начать с самого начала или перейти вперед, ознакомьтесь с остальными статьями в меню с содержанием серии выше, в начале статьи.
Классификация с помощью однослойного перцептрона
В предыдущей статье была представлена простая задача классификации, которую мы рассмотрели с точки зрения обработки сигналов на базе нейросети. Математическая связь, необходимая для этой задачи, была настолько простой, что я смог спроектировать сеть, просто подумав о том, как определенный набор весов позволил бы выходному узлу правильно классифицировать входные данные.
Это сеть, которую я разработал:
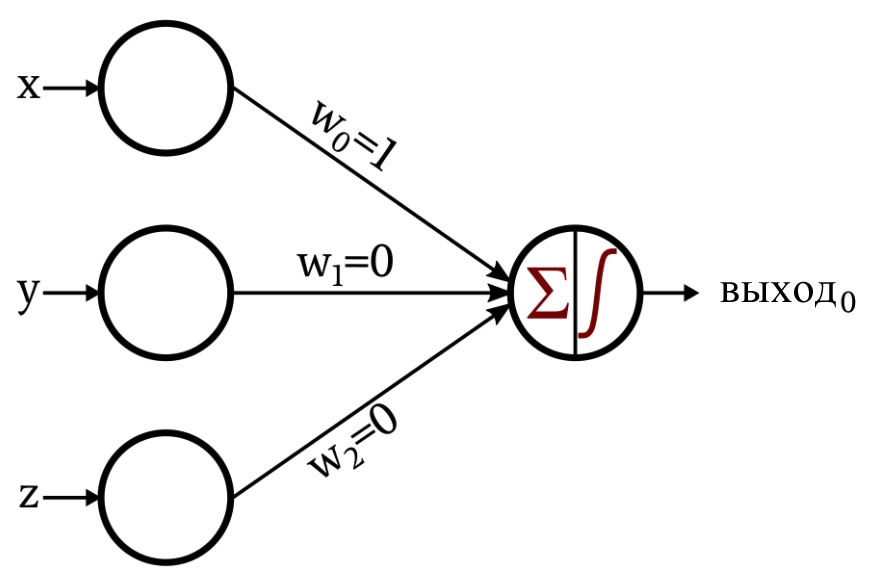
Функция активации в выходном узле – это единичная ступенчатая функция:
\[f(x)=\begin{cases}0 & x < 0\\1 & x \geq 0\end{cases}\]
Обсуждение стало немного интереснее, когда я представил сеть, которая создала свои собственные веса с помощью процедуры, известной как обучение:
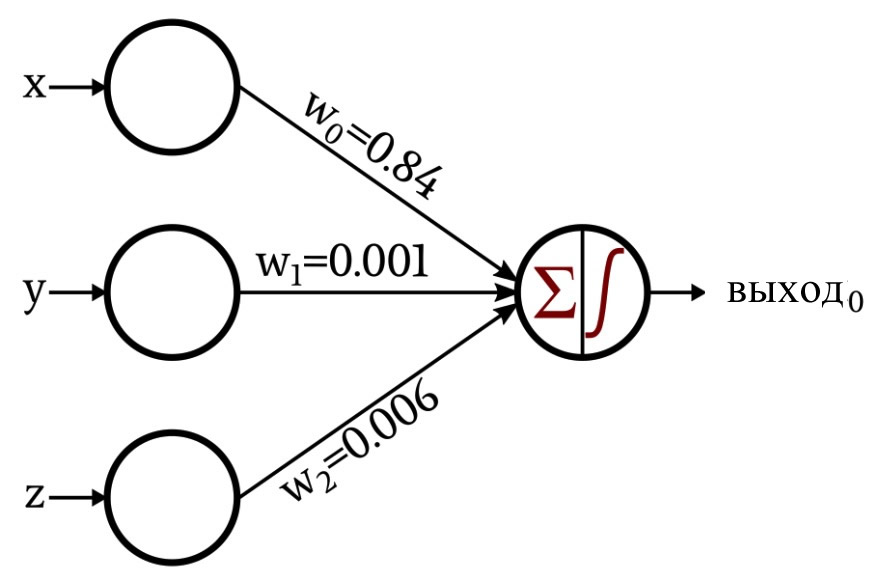
В оставшейся части данной статьи мы рассмотрим код на Python, который я использовал для получения этих весов.
Нейронная сеть на Python
Ниже приведен код:
import pandas
import numpy as np
input_dim = 3
learning_rate = 0.01
Weights = np.random.rand(input_dim)
#Weights[0] = 0.5
#Weights[1] = 0.5
#Weights[2] = 0.5
Training_Data = pandas.read_excel("3D_data.xlsx")
Expected_Output = Training_Data.output
Training_Data = Training_Data.drop(['output'], axis=1)
Training_Data = np.asarray(Training_Data)
training_count = len(Training_Data[:,0])
for epoch in range(0,5):
for datum in range(0, training_count):
Output_Sum = np.sum(np.multiply(Training_Data[datum,:], Weights))
if Output_Sum < 0:
Output_Value = 0
else:
Output_Value = 1
error = Expected_Output[datum] - Output_Value
for n in range(0, input_dim):
Weights[n] = Weights[n] + learning_rate*error*Training_Data[datum,n]
print("w_0 = %.3f" %(Weights[0]))
print("w_1 = %.3f" %(Weights[1]))
print("w_2 = %.3f" %(Weights[2]))
Давайте внимательнее посмотрим на эти инструкции.
Настройка сети и организация данных
input_dim = 3
Размерность регулируется. Наши входные данные, если вы помните, состоят из трехмерных координат, поэтому нам необходимо три входных узла. Эта программа не поддерживает несколько выходных узлов, но мы включим регулируемую выходную размерность в будущем эксперименте.
learning_rate = 0.01
Мы обсудим скорость обучения в следующей статье.
Weights = np.random.rand(input_dim)
#Weights[0] = 0.5
#Weights[1] = 0.5
#Weights[2] = 0.5
Веса обычно инициализируются случайными значениями. Функция numpy random.rand() генерирует массив длиной input_dim, заполненный случайными значениями, распределенными в интервале [0, 1). Однако начальные значения веса влияют на конечные значения веса, полученные в результате процедуры обучения, поэтому, если вы хотите оценить влияние других переменных (таких как размер обучающего набора или скорость обучения), вы можете устранить этот мешающий фактор, установив все веса в значение известной константы вместо случайно сгенерированного числа.
Training_Data = pandas.read_excel("3D_data.xlsx")
Я использую библиотеку pandas для импорта обучающих данных из электронной таблицы Excel. Следующая статья более подробно расскажет о тренировочных данных.
Expected_Output = Training_Data.output
Training_Data = Training_Data.drop(['output'], axis=1)
Набор обучающих данных включает в себя входные значения и соответствующие выходные значения. Первая инструкция выделяет выходные значения и сохраняет их в отдельном массиве, а следующая инструкция удаляет выходные значения из исходного набора обучающих данных.
Training_Data = np.asarray(Training_Data)
training_count = len(Training_Data[:,0])
Я преобразую набор обучающих данных, который в настоящее время является структурой данных pandas, в массив numpy, а затем просматриваю длину одного из столбцов, чтобы определить, сколько точек данных доступно для обучения.
Расчет выходных значений
for epoch in range(0,5):
Продолжительность одной тренировки определяется количеством доступных обучающих данных. Тем не менее, вы можете продолжить оптимизацию весов, обучая нейросеть несколько раз, используя один и тот же набор данных – преимущества обучения не исчезают просто потому, что нейросеть уже видела эти обучающие данные. Каждый полный проход через весь обучающий набор называется эпохой.
for datum in range(0, training_count):
Процедура, содержащаяся в этом цикле, выполняется один раз для каждой строки в обучающем наборе, где «строка» относится к группе значений входных данных и соответствующему выходному значению (в нашем случае входная группа состоит из трех чисел, представляющих компоненты x, y и z точки в трехмерном пространстве).
Output_Sum = np.sum(np.multiply(Training_Data[datum,:], Weights))
Выходной узел должен суммировать значения, полученные тремя входными узлами. Моя реализация на Python делает это, сначала выполняя поэлементное умножение массива Training_Data на массив Weights, а затем вычисляя сумму элементов в массиве, полученном этим умножением.
if Output_Sum < 0:
Output_Value = 0
else:
Output_Value = 1
Оператор if-else применяет единичную ступенчатую функцию активации: если сумма меньше нуля, значение, сгенерированное выходным узлом, равно 0; если сумма равна или больше нуля, выходное значение равно единице.
Обновление весов
Когда первый расчет выходных значений завершен, у нас есть весовые значения, но они не помогли нам достичь правильной классификации, потому что они были сгенерированы случайным образом. Мы превращаем нейронную сеть в эффективную систему классификации, многократно изменяя веса таким образом, чтобы они постепенно отражали математическое соотношение между входными данными и искомыми выходными значениями. Изменение веса достигается путем применения следующего правила обучения для каждой строки в обучающем наборе:
\[w_{новый} = w+(\alpha\times(выход_{ожидаемый}-выход_{рассчитанный})\times вход)\]
Символ α обозначает скорость обучения. Таким образом, чтобы вычислить новое значение веса, мы умножаем соответствующее входное значение на скорость обучения и на разницу между ожидаемым выходным значением (которое обеспечивается обучающим набором) и рассчитанным выходным значением, а затем результат этого умножения. добавляется к текущему значению веса. Если мы определим дельту \((\delta)\) как \((выход_{ожидаемый}-выход_{рассчитанный})\), мы можем переписать формулу как
\[w_{новый} = w+(\alpha\times\delta\times вход)\]
Вот как я реализовал это правило обучения на Python:
error = Expected_Output[datum] - Output_Value
for n in range(0, input_dim):
Weights[n] = Weights[n] + learning_rate*error*Training_Data[datum,n]
Заключение
Теперь у вас есть код, который вы можете использовать для обучения однослойного перцептрона с одним выходным узлом. Более подробно о теории и практике обучения нейронных сетей мы расскажем в следующей статье.
