Добавление узлов смещения в нейронную сеть
В данной статье показано, как добавить значения смещения в многослойный перцептрон, реализованный на языке программирования высокого уровня, таком как Python.
Добро пожаловать в серию статей о нейронных сетях. Прежде чем вы перейдете к этой статье об узлах смещения, попробуйте наверстать упущенное в остальных статьях, которые можно увидеть выше, в меню с содержанием.
Узлы смещения, которые могут быть добавлены к входному или скрытому слою перцептрона, создают постоянное значение, которое выбирает разработчик.
Мы обсуждали значения смещения еще в 11-ой статье, и, если вам непонятно, что такое узлы смещения, или как они изменяют и потенциально улучшают функциональность нейронной сети, я советую вам прочитать (или перечитать) соответствующий фрагмент этой статьи.
В данной статье я сначала объясню два метода включения значений смещения в архитектуру нейросети, а затем мы проведем эксперимент, чтобы выяснить, могут ли значения смещения улучшить показатели точности, которые мы получили в предыдущей (в 16-ой) статье.
Включение смещения через электронную таблицу
Следующая диаграмма изображает нейросеть, у которой узел смещения находится во входном слое, а не в скрытом слое.
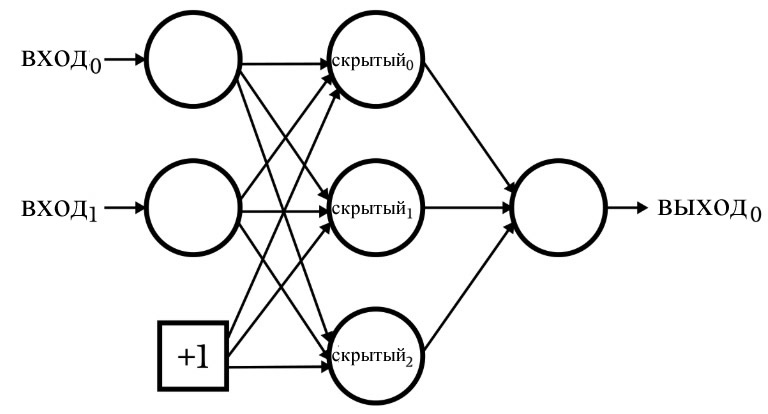
Если эта конфигурация – именно то, что вам нужно, то вы можете добавить значение смещения, используя электронную таблицу, содержащую ваши данные обучения или проверки.
Преимущество этого метода состоит в том, что не требуется никаких существенных изменений кода. Первым шагом является вставка столбца в таблицу и заполнение его значением смещения:
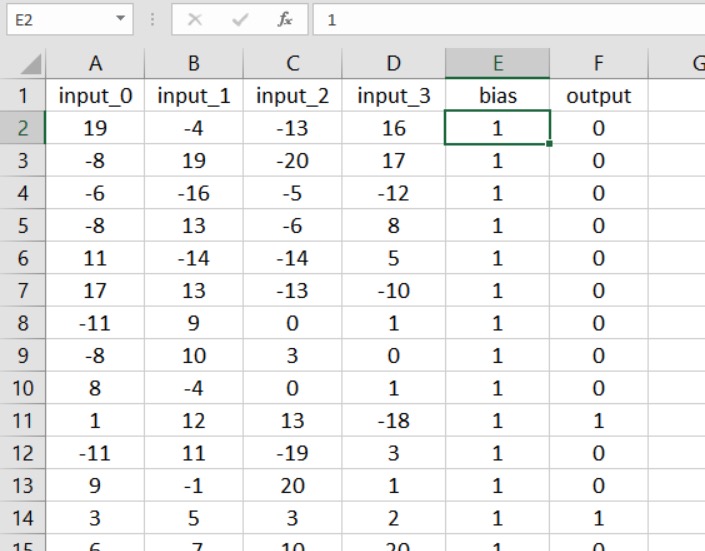
Теперь всё, что вам нужно сделать, – это увеличить размерность входного слоя на единицу:
LR = 0.1
#I_dim = 4 # без смещения
I_dim = 5 # со смещением
H_dim = 7
epoch_count = 1
#np.random.seed(1)
Интеграция смещения в код
Если вам нужен узел смещения в скрытом слое или вам не нравится работать с электронными таблицами, вам понадобится другое решение.
Давайте предположим, что мы хотим добавить узел смещения как к входному слою, так и к скрытому слою. Во-первых, нам нужно увеличить I_dim и H_dim, поскольку нам необходимо внедрить узлы смещения таким образом, чтобы они действовали как обычные узлы, но с предустановленным значением, которое выбирает разработчик и которое никогда не изменяется.
Я сделаю это следующим образом:
LR = 0.1
input_bias = 1 # 0 - если нет смещения, 1 - смещение включено
hidden_bias = 1 # 0 - если нет смещения, 1 - смещение включено
I_dim = 4
H_dim = 7
epoch_count = 1
Создание узла смещения во входном слое
Как вы помните, для сборки набора обучающих данных, разделения целевых выходных значений и извлечения количества обучающих выборок мы используем следующий код.
training_data = pandas.read_excel('MLP_Tdata4.xlsx')
target_output = training_data.output
training_data = training_data.drop(['output'], axis=1)
training_data = np.asarray(training_data)
training_count = len(training_data[:,0])
После этих операций количество столбцов в двумерном массиве training_data будет равно количеству входных столбцов в электронной таблице. Нам нужно увеличить количество столбцов на один, чтобы учесть узел смещения во входном слое, и пока мы это делаем, мы можем заполнить этот дополнительный столбец требуемым значением смещения.
Следующий код показывает, как это можно сделать.
validation_count = len(validation_data[:,0])
if input_bias:
new_column = np.ones((training_count, 1))
training_data = np.hstack((training_data, new_column))
new_column = np.ones((validation_count, 1))
validation_data = np.hstack((validation_data, new_column))
Функция np.ones() создает массив из одного столбца, число строк которого равно training_count, и присваивает значение +1 каждому элементу в этом массиве. Затем мы используем функцию np.hstack(), чтобы добавить этот массив из одного столбца справа к исходному массиву training_data.
Обратите внимание, что я выполнил эту процедуру как для данных обучения, так и для данных проверки. Важно помнить, что цель на самом деле состоит не в том, чтобы изменить данные обучения или проверки; скорее, мы модифицируем данные как средство реализации необходимой конфигурации сети.
Когда мы смотрим на блок-схему перцептрона, узлы смещения появляются в ней как элементы самой сети; таким образом, любые выборки, которые обрабатываются нейросетью, должны подвергаться этой модификации.
Создание узла смещения в скрытом слое
Мы можем добавить смещение в обработку прямого распространения, изменив цикл for, который вычисляет значения постактивации скрытого слоя, а затем вручную вставить значение смещения для последнего скрытого узла (который на самом деле является узлом смещения).
Первая модификация показана ниже:
for sample in range(training_count):
for node in range(H_dim - hidden_bias):
preActivation_H[node] = np.dot(training_data[sample,:], weights_ItoH[:, node])
postActivation_H[node] = logistic(preActivation_H[node])
Если нейросеть настроена на отсутствие узла смещения в скрытом слое, hidden_bias равно 0, выполнение цикла for не изменяется.
Если, наоборот, мы решили включить узел смещения в скрытый слой, цикл for не будет вычислять значение постактивации для последнего узла в слое (то есть узла смещения).
Следующим шагом является увеличение переменной узла, чтобы она обращалась к узлу смещения в массиве postActivation_H, а затем присваивала значение смещения.
postActivation_H[node] = logistic(preActivation_H[node])
if hidden_bias:
node += 1
postActivation_H[node] = 1
preActivation_O = np.dot(postActivation_H, weights_HtoO)
Обратите внимание, что эти изменения должны быть применены и к проверочной части кода.
Значения смещения, отличающиеся от +1
По моему опыту, +1 – это стандартное значение смещения, и я не знаю, есть ли какое-либо веское обоснование для использования других чисел. Смещение изменяется весами, поэтому выбор +1 не накладывает жестких ограничений на то, как смещение взаимодействует с общим функционалом нейросети.
Однако, если вы хотите поэкспериментировать с другими значениями смещения, вы можете легко это сделать. Для смещения в скрытом слое вы просто меняете число, присвоенное postActivation_H[node]. Для смещения во входном слое вы можете умножить массив new_column (каждый элемент которого изначально равен +1) на необходимое значение смещения.
Тестирование влияния смещения
Если вы читали 16-ую статью, вы знаете, что моему перцептрону было трудно классифицировать выборки в эксперименте № 3, который был задачей «высокой сложности».
Давайте посмотрим, предлагает ли добавление одного или нескольких узлов смещения устойчивое и значительное улучшение.
Я предполагал, что различия в точности классификации будут довольно незначительными, поэтому в этом эксперименте я усреднил десять запусков вместо пяти. Наборы данных обучения и проверки были сгенерированы с использованием одной и той же связи высокой сложности между входом и выходом, а размерность скрытого слоя была равна 7.
Результаты:
| Средняя точность | Минимальная точность | Максимальная точность | |
|---|---|---|---|
| без смещения | 92,45% | 89,42% | 94,18% |
| смещение только во входном слое | 92,25% | 89,48% | 96,02% |
| смещение только в скрытом слое | 92,05% | 89,50% | 93,32% |
| смещение и во входном, и в скрытом слоях | 92,19% | 89,28% | 95,70% |
Заключение
Как видите, узлы смещения не привели к каким-либо значительным изменениям в эффективности классификации.
Это на самом деле меня не удивляет – я думаю, что узлы смещения иногда немного переоцениваются, и, учитывая природу входных данных, которые я использовал в этом эксперименте, я не вижу причин, почему узлы смещения могли бы помочь.
Тем не менее, смещение является важной техникой в некоторых приложениях; будет хорошей идеей, написать код, поддерживающий функциональность узлов смещения, чтобы они были там, когда вам понадобятся.
