Как увеличить точность скрытого слоя нейронной сети
В данной статье мы проведем некоторые эксперименты по классификации и соберем данные о взаимосвязи между размерностью скрытого слоя и производительностью сети. А также рассмотрим, как изменить скрытый слой для повышения точности нейронной сети, используя реализацию на Python и примеры задач.
Количество узлов, включенных в скрытый слой, влияет на способности классификации и скорость нейронной сети перцептрон. Мы собираемся провести эксперименты, которые помогут нам сформулировать некоторые интуитивно возникающие подозрения о том, как размерность скрытого слоя вписывается в попытку спроектировать нейросеть, которая обучается в течение приемлемого промежутка времени, производит выходные значения с приемлемой задержкой и отвечает требованиям точности.
Сравнение эффективности на Python
Код нейронной сети на Python, представленный в 12-ой статье, уже содержит раздел, в котором рассчитывается точность обученной нейросети при классификации выборок из проверочного набора данных. Таким образом, всё, что нам нужно сделать, это добавить код, который будет сообщать время выполнения для обучения (которое включает в себя операции прямого и обратного распространения) и для реальной работы по классификации (которая включает только операцию прямого распространения). Для этого мы будем использовать функцию time.perf_counter().
Вот как я отмечаю начало и конец обучения:
#####################
# обучение
#####################
t_trainingstart = time.perf_counter()
for epoch in range(epoch_count):
weights_HtoO[H_node] -= LR * gradient_HtoO
t_trainingstop = time.perf_counter()
#####################
# проверка
#####################
Время начала и окончания валидации генерируется так же:
#####################
# проверка
#####################
t_validationstart = time.perf_counter()
correct_classification_count = 0
correct_classification_count += 1
t_validationstop = time.perf_counter()
print('Percentage of correct classifications:')
Два измерения времени обработки представлены следующим образом:
print('Percentage of correct classifications:')
print(correct_classification_count*100/validation_count)
print('Training time:')
print(t_trainingstop - t_trainingstart)
print('Validation time:')
print(t_validationstop - t_validationstart)
Обучающие данные и методика измерений
Нейронная сеть будет выполнять классификацию истина/ложь для входных выборок, состоящих из четырех числовых значений от –20 до +20.
Таким образом, у нас есть четыре входных узла и один выходной узел, а входные значения генерируются с помощью формулы в Excel, показанной ниже.
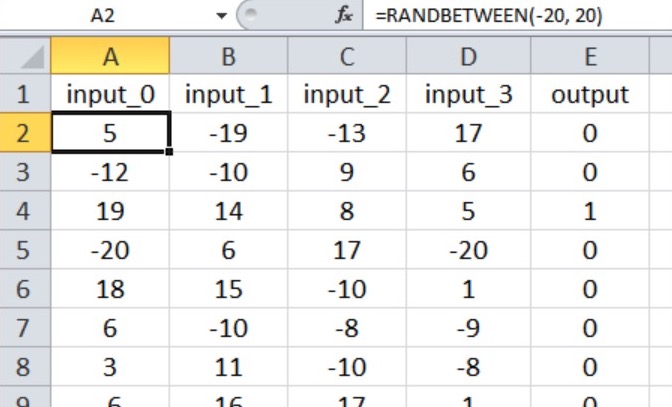
Мой набор обучающих данных состоит из 40000 выборок, а проверочный набор – из 5000 выборок. Скорость обучения составляет 0,1, и я выполняю только одну обучающую эпоху.
Мы выполним три эксперимента, представляющих связи вход-выход различной степени сложности. Инструкция np.random.seed(1) закомментирована, поэтому начальные значения весов будут различаться, а, следовательно, и точность классификации.
В каждом эксперименте программа будет выполняться пять раз (с одними и теми же данными обучения и проверки) для каждой размерности скрытого слоя, а окончательные измерения точности и времени обработки будут представлять собой среднее арифметическое этих результатов, полученных при пяти отдельных запусках.
Эксперимент 1: задача низкой сложности
В этом эксперименте выходные данные имеют значение true, только если первые три входных сигнала больше нуля, как показано ниже, на скриншоте Excel (обратите внимание, что четвертый вход не влияет на выходное значение).
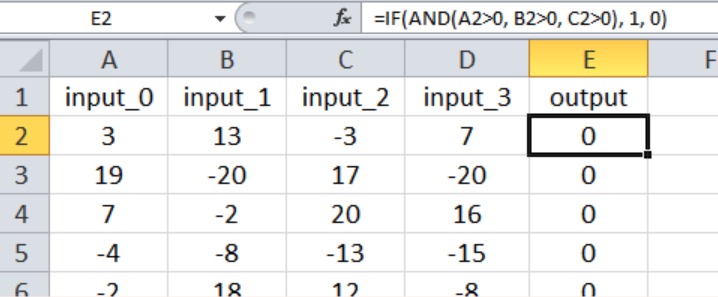
Думаю, что эту связь вход-выход можно квалифицировать как довольно простую для многослойного перцептрона.
Основываясь на рекомендациях, которые я предоставил в 15-ой статье относительно того, сколько слоев и узлов требуется нейронной сети, я бы начал с размерности скрытого слоя, равной двум третям входной размерности.
Поскольку у меня не может быть скрытого слоя с дробным количеством узлов, я начну с H_dim = 2. В таблице ниже представлены результаты.
| Точность классификации | Время обучения, с | Время валидации, с | |
|---|---|---|---|
| 2 скрытых узла | 88,83% | 3,856 | 0,014 |
| 3 скрытых узла | 93,96% | 5,386 | 0,173 |
| 4 скрытых узла | 96,60% | 7,246 | 0,190 |
| 5 скрытых узлов | 98,23% | 8,693 | 0,218 |
Мы видим улучшение классификации вплоть до пяти скрытых узлов. Тем не менее, я думаю, что эти значения преувеличивают выгоду от увеличения количества скрытых узлов с четырех до пяти, потому что точность одного из запусков с четырьмя скрытыми узлами составила 88,6%, и это снизило среднее значение.
Если я исключу этот запуск с низкой точностью, средняя точность для четырех скрытых узлов будет на самом деле немного выше, чем средняя для пяти скрытых узлов. Я подозреваю, что в этом случае четыре скрытых узла обеспечат наилучший баланс между точностью и скоростью.
Еще одна важная вещь, которую следует отметить в этих результатах, – это различие в том, как размерность скрытого слоя влияет на время обучения и время обработки. Переход с двух до четырех скрытых узлов увеличивает время валидации в 1,3 раза, но при этом время обучения увеличивается в 1,9 раза.
Обучение значительно сложнее в вычислительном отношении, чем обработка с прямым распространением, поэтому мы должны помнить о том, как конфигурация сети влияет на нашу способность обучать нейросеть за приемлемое время.
Эксперимент 2: задача умеренной сложности
На скриншоте Excel показана связь вход-выход. Теперь на выходное значение влияют все четыре входа, и связи не так просты, как в эксперименте 1.
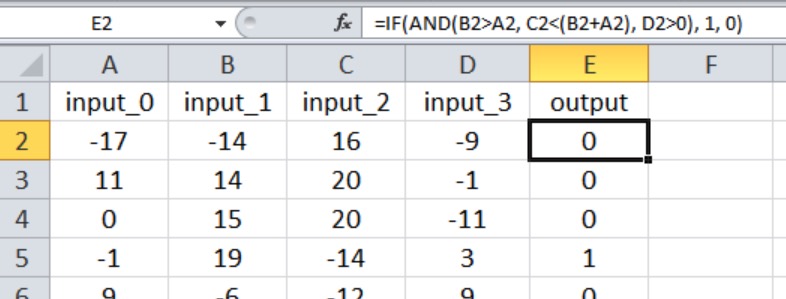
Я начал с трех скрытых узлов. Ниже показаны результаты:
| Точность классификации | Время обучения, с | Время валидации, с | |
|---|---|---|---|
| 3 скрытых узла | 91,76% | 5,465 | 0,171 |
| 4 скрытых узла | 96,64% | 7,022 | 0,192 |
| 5 скрытых узлов | 98,74% | 8,621 | 0,235 |
| 6 скрытых узлов | 98,70% | 10,080 | 0,252 |
В этом случае я подозреваю, что пять скрытых узлов дадут нам наилучшее сочетание точности и скорости, хотя в очередной раз при запусках для четырех скрытых узлов было получено одно значение точности, которое было значительно ниже, чем другие. Если вы проигнорируете этот выброс, результаты для четырех, пяти и шести скрытых узлов будут выглядеть очень похожими.
Тот факт, что запуски с пятью и шестью скрытыми узлами не породили каких-либо выбросов, приводит нас к возможно интересному открытию: возможно, увеличение размерности скрытого слоя делает сеть более устойчивой к условиям, которые по какой-то причине делают обучение особенно сложным.
Эксперимент 3: задача высокой сложности
Как показано ниже, новая связь вход-выход снова использует все четыре входных значения, и мы ввели нелинейность, возведя в квадрат один из входных сигналов и взяв квадратный корень из другого.
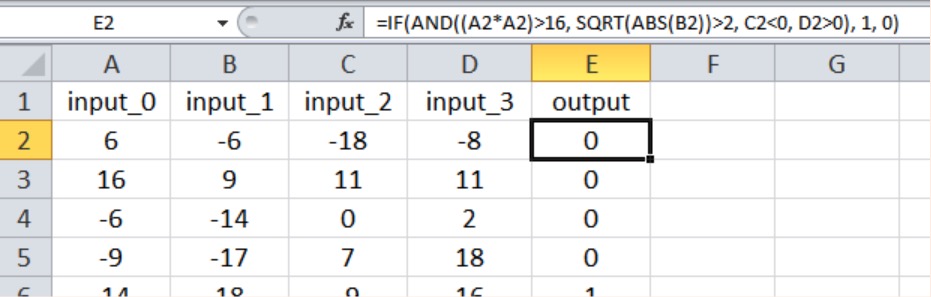
Вот результаты:
| Точность классификации | Время обучения, с | Время валидации, с | |
|---|---|---|---|
| 4 скрытых узла | 89,92% | 6,960 | 0,191 |
| 5 скрытых узлов | 91,06% | 8,718 | 0,225 |
| 6 скрытых узлов | 91,64% | 10,086 | 0,254 |
| 7 скрытых узлов | 92,38% | 11,788 | 0,274 |
У нейросети определенно было больше трудностей с этими математическими связями более высокой сложности; даже с семью скрытыми узлами точность была ниже, чем только с тремя скрытыми узлами в задаче низкой сложности. Я уверен, что мы могли бы улучшить производительность для задачи высокой сложности, изменив другие параметры нейросети, например, смещение (смотрите 11-ую статью) или «отжиг» (annealing) скорости обучения (смотрите 6-ую статью).
Тем не менее, я сохраню размерность скрытого уровня на уровне семи, пока не буду убежден, что другие усовершенствования могут позволить нейросети поддерживать адекватную производительность с меньшим скрытым уровнем.
Заключение
Мы рассмотрели несколько интересных измерений, которые создают довольно четкую картину взаимосвязи между размерностью скрытого слоя и производительностью перцептрона. Конечно, есть еще много деталей, которые мы могли бы изучить, но я думаю, что эти эксперименты дают вам базовую информацию, на которую можно опираться, для экспериментов с проектированием и обучением нейронных сетей.
