Как создать нейронную сеть многослойный перцептрон на Python
Данная статья шаг за шагом проведет вас по программе на Python, которая позволит нам обучить нейронную сеть и выполнить сложную классификацию.
Это 12-я статья в серии о разработке нейронных сетей. С остальными статьями вы можете ознакомиться выше, в меню с содержанием.
В данной статье мы применим знания, полученные нами при изучении нейронных сетей перцептрон, и узнаем, как реализовать нейросеть на знакомом языке: Python.
Разработка понятного кода на Python для нейронных сетей
Недавно я просмотрел немало онлайн-ресурсов по нейронным сетям, и, хотя, несомненно, в них есть много полезной информации, я не был удовлетворен найденными мною программными реализациями. Они всегда были или слишком сложными, или недостаточно интуитивно понятными. Когда я писал свою нейронную сеть на Python, я на самом деле хотел сделать что-то, что могло бы помочь людям узнать о том, как работает система, и как теория нейронных сетей переводится на язык программных инструкций.
Однако иногда между ясностью и эффективностью кода существует обратная зависимость. Программа, которую мы обсудим в этой статье, однозначно не оптимизирована для быстрой работы. Оптимизация является серьезной проблемой в области нейронных сетей; реальные приложения могут потребовать огромного количества обучения, и, следовательно, тщательная оптимизация может привести к значительному сокращению времени обработки. Тем не менее, для простых экспериментов, подобных тем, которые мы будем проводить, обучение не займет много времени, и нет оснований делать упор на методиках программирования, которые способствуют скорости, а не простоте и понятности.
Полный код программы на Python приведен в конце статьи. Код выполняет как обучение, так и проверку. Данная статья посвящена обучению, а валидацию мы обсудим позже. В любом случае, во фрагменте программы, выполняющем проверку, не так много функционала, который не покрыт во фрагменте, выполняющем обучение.
Размышляя над кодом, вы, возможно, захотите оглянуться на немного сумбурную, но очень информативную диаграмму архитектуры плюс терминологии, которую я представил в части 10.
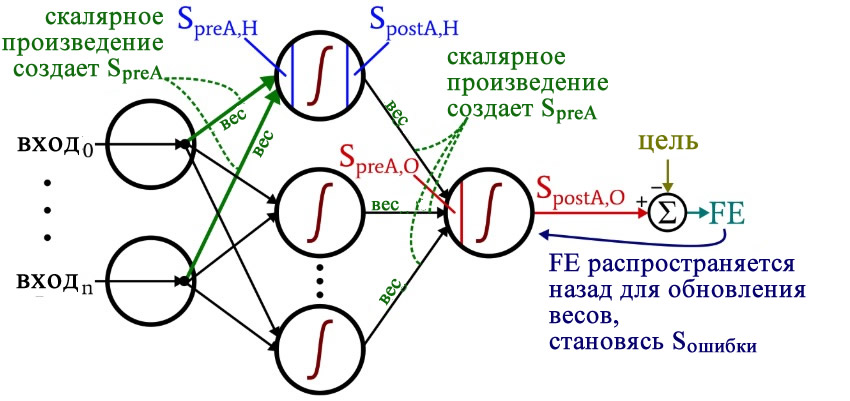
Подготовка функций и переменных
import pandas
import numpy as np
def logistic(x):
return 1.0/(1 + np.exp(-x))
def logistic_deriv(x):
return logistic(x) * (1 - logistic(x))
LR = 1
I_dim = 3
H_dim = 4
epoch_count = 1
#np.random.seed(1)
weights_ItoH = np.random.uniform(-1, 1, (I_dim, H_dim))
weights_HtoO = np.random.uniform(-1, 1, H_dim)
preActivation_H = np.zeros(H_dim)
postActivation_H = np.zeros(H_dim)
Библиотека NumPy широко используется для расчетов в нейросети, а библиотека Pandas дает мне удобный способ импортировать данные обучения из файла Excel.
Как вы уже знаете, для активации мы используем функцию логистической сигмоиды. Для расчета значений постактивации нам нужна сама логистическая функция, а для обратного распространения необходима производная логистической функции.
Затем мы выбираем скорость обучения, размерность входного слоя, размерность скрытого слоя и количество эпох. Для реальных нейронных сетей важно обучение в течение нескольких эпох, потому что это позволяет вам извлечь больше информации из ваших обучающих данных. Когда вы генерируете обучающие данные в Excel, вам не нужно запускать несколько эпох, потому что вы можете легко создать больше обучающих выборок.
Функция np.random.uniform() заполняет наши две матрицы весов случайными значениями от –1 до +1 (обратите внимание, что матрица весов между скрытым и выходным слоями на самом деле представляет собой просто массив, поскольку у нас только один выходной узел). Оператор np.random.seed(1) приводит к тому, что случайные значения становятся одинаковыми при каждом запуске программы. Начальные значения весов могут оказать существенное влияние на конечную производительность обученной сети, поэтому, если вы пытаетесь оценить, как другие переменные улучшают или ухудшают производительность, вы можете раскомментировать эту инструкцию и тем самым устранить влияние случайной инициализации весовых коэффициентов.
И в конце я создаю пустые массивы для значений преактивации и постактивации в скрытом слое.
Импорт обучающих данных
training_data = pandas.read_excel('MLP_Tdata.xlsx')
target_output = training_data.output
training_data = training_data.drop(['output'], axis=1)
training_data = np.asarray(training_data)
training_count = len(training_data[:,0])
Это та же процедура, которую я использовал в части 3. Я импортирую обучающие данные из Excel, отделяю целевые значения в столбце «output», удаляю столбец «output», преобразую обучающие данные в матрицу NumPy и сохраняю количество обучающих выборок в переменной training_count.
Обработка прямого распространения
Вычисления, которые создают выходное значение, и в которых данные перемещаются слева направо на типовой схеме нейронной сети, составляют фрагмент «прямого распространения» работы системы. Вот код «прямого распространения»:
#####################
# обучение
#####################
for epoch in range(epoch_count):
for sample in range(training_count):
for node in range(H_dim):
preActivation_H[node] = np.dot(training_data[sample,:], weights_ItoH[:, node])
postActivation_H[node] = logistic(preActivation_H[node])
preActivation_O = np.dot(postActivation_H, weights_HtoO)
postActivation_O = logistic(preActivation_O)
FE = postActivation_O - target_output[sample]
Первый цикл for позволяет нам проходить через несколько эпох. Внутри каждой эпохи, во втором цикле for, поочередно проходя по выборкам, мы вычисляем выходное значение для каждой выборки (то есть сигнал постактивации выходного узла). В третьем цикле for мы обращаемся индивидуально к каждому скрытому узлу, используя скалярное произведение для генерирования сигнала преактивации и функцию активации для генерирования сигнала постактивации.
После этого мы готовы вычислить сигнал преактивации для выходного узла (снова используя скалярное произведение), и мы применяем функцию активации для генерирования сигнала постактивации. Затем, чтобы вычислить итоговую ошибку, мы вычитаем целевое значение из значения полученного сигнала постактивации выходного узла.
Обратное распространение
После того, как мы выполнили расчеты для прямого распространения, настало время изменить направление. Во фрагменте программы с обратным распространением мы перемещаемся к весам от скрытых узлов к выходному узлу, а затем к весам от входного слоя к скрытому слою, перенося при этом информацию об ошибке для эффективного обучения сети.
for H_node in range(H_dim):
S_error = FE * logistic_deriv(preActivation_O)
gradient_HtoO = S_error * postActivation_H[H_node]
for I_node in range(I_dim):
input_value = training_data[sample, I_node]
gradient_ItoH = S_error * weights_HtoO[H_node] * logistic_deriv(preActivation_H[H_node]) * input_value
weights_ItoH[I_node, H_node] -= LR * gradient_ItoH
weights_HtoO[H_node] -= LR * gradient_HtoO
У нас есть два слоя для циклов for: один для весовых коэффициентов между скрытым и выходным слоями и один для весовых коэффициентов между входным и скрытым слоями. Сначала мы генерируем сигнал ошибки (Sошибки, S_error), который нам нужен для вычисления обоих градиентов, gradient_HtoO (от скрытого слоя к выходному) и gradient_ItoH (от входного слоя к скрытому), а затем мы обновляем весовые коэффициенты, вычитая градиент, умноженный на скорость обучения.
Обратите внимание, как веса между входным и скрытым слоями обновляются внутри цикла для значений между скрытым и выходным слоями. Мы начинаем с сигнала ошибки, который ведет обратно к одному из скрытых узлов, затем распространяем этот сигнал ошибки на все входные узлы, которые подключены к одному конкретному скрытому узлу:
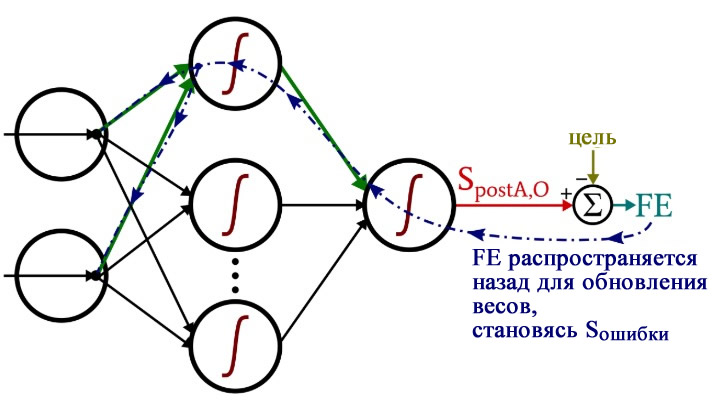
После того, как все весовые коэффициенты (как ItoH (от входного слоя к скрытому), так и HtoO (от скрытого слоя к выходному)), связанные с этим одним скрытым узлом, были обновлены, мы возвращаемся к началу и начинаем снова для следующего скрытого узла.
Также обратите внимание, что веса ItoH модифицируются перед весами HtoO. Мы используем текущий вес HtoO при расчете градиента, поэтому до выполнения расчетов мы не хотим изменять веса HtoO.
Заключение
Интересно задуматься о том, сколько теории ушло в эту относительно короткую программу на Python. Я надеюсь, что этот код на самом деле поможет вам понять, как мы можем программно реализовать нейронную сеть многослойный перцептрон.
Ниже приведен полный код программы.
import pandas
import numpy as np
def logistic(x):
return 1.0/(1 + np.exp(-x))
def logistic_deriv(x):
return logistic(x) * (1 - logistic(x))
LR = 1
I_dim = 3
H_dim = 4
epoch_count = 1
#np.random.seed(1)
weights_ItoH = np.random.uniform(-1, 1, (I_dim, H_dim))
weights_HtoO = np.random.uniform(-1, 1, H_dim)
preActivation_H = np.zeros(H_dim)
postActivation_H = np.zeros(H_dim)
training_data = pandas.read_excel('MLP_Tdata.xlsx')
target_output = training_data.output
training_data = training_data.drop(['output'], axis=1)
training_data = np.asarray(training_data)
training_count = len(training_data[:,0])
validation_data = pandas.read_excel('MLP_Vdata.xlsx')
validation_output = validation_data.output
validation_data = validation_data.drop(['output'], axis=1)
validation_data = np.asarray(validation_data)
validation_count = len(validation_data[:,0])
#####################
# обучение
#####################
for epoch in range(epoch_count):
for sample in range(training_count):
for node in range(H_dim):
preActivation_H[node] = np.dot(training_data[sample,:], weights_ItoH[:, node])
postActivation_H[node] = logistic(preActivation_H[node])
preActivation_O = np.dot(postActivation_H, weights_HtoO)
postActivation_O = logistic(preActivation_O)
FE = postActivation_O - target_output[sample]
for H_node in range(H_dim):
S_error = FE * logistic_deriv(preActivation_O)
gradient_HtoO = S_error * postActivation_H[H_node]
for I_node in range(I_dim):
input_value = training_data[sample, I_node]
gradient_ItoH = S_error * weights_HtoO[H_node] * logistic_deriv(preActivation_H[H_node]) * input_value
weights_ItoH[I_node, H_node] -= LR * gradient_ItoH
weights_HtoO[H_node] -= LR * gradient_HtoO
#####################
# проверка
#####################
correct_classification_count = 0
for sample in range(validation_count):
for node in range(H_dim):
preActivation_H[node] = np.dot(validation_data[sample,:], weights_ItoH[:, node])
postActivation_H[node] = logistic(preActivation_H[node])
preActivation_O = np.dot(postActivation_H, weights_HtoO)
postActivation_O = logistic(preActivation_O)
if postActivation_O > 0.5:
output = 1
else:
output = 0
if output == validation_output[sample]:
correct_classification_count += 1
print('Percentage of correct classifications:')
print(correct_classification_count*100/validation_count)
