Сигмоидная функция активации: активация в нейронных сетях многослойный перцептрон
В данной статье мы увидим, почему для нейронной сети, которая обучается посредством градиентного спуска, нам нужна новая функция активации.
Добро пожаловать в серию статей о нейросетях, написанных Робертом Кеймом. Если вы пропустили что-то из этой серии, то можете наверстать упущенное, используя меню с содержанием в начале статьи.
В данной статье вы узнаете о функциях активации, в том числе об ограничениях, связанных с единичными ступенчатыми функциями активации, и о том, как сигмоидная функция активации может снять эти ограничения в нейронных сетях многослойный перцептрон.
Почему единичные ступенчатые функции активации не подходят для многослойных перцептронов
До сих пор в этой серии статей мы использовали единичную ступенчатую функцию активации:
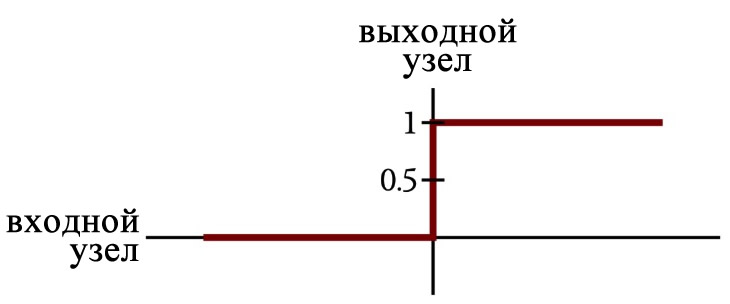
Вычислительные узлы нейросети суммировали все взвешенные значения, полученные от предыдущего слоя, а затем преобразовали эти суммы в единицу или ноль в соответствии со следующим выражением:
\[f(x)=\begin{cases}0 & x < 0\\1 & x \geq 0\end{cases}\]
Однако вы, возможно, заметили, что на моих диаграммах нейросетей представление функции активации не похоже на единичную ступенчатую функцию. Это больше похоже на сглаженную, не совсем вертикальную версию единичной ступенчатой функции:
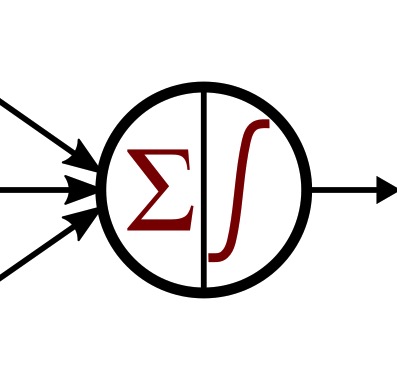
Эта сглаженная версия, на мой взгляд, выглядит более красиво, но это не та причина, по которой я ее выбрал. Или, по крайней мере, это не единственная причина. Оказывается, что единичная ступенчатая функция не очень хорошо подходит для использования в качестве функции активации в многослойных перцептронах.
Давайте выясним, почему.
Градиентный спуск со средней квадратичной ошибкой
Средняя квадратичная ошибка – это наша функция ошибки, а обновление весов с помощью градиентного спуска требует, чтобы мы нашли частную производную функции ошибки по отношению к весу, который мы хотим обновить. Выполнение этого дифференцирования показывает, что градиент ошибки по отношению к весу задается выражением, которое включает в себя производную функции активации.
Единичная ступенчатая функция позволяет использовать внутри узла очень простые вычисления (всё, что вам нужно, это оператор if/else), но это преимущество становится бессмысленным в контексте градиентного спуска, поскольку единичная ступенчатая функция не дифференцируема – она не является непрерывной функцией, а наклон в точке, где выходной сигнал переходит от нуля к единице, равен бесконечности.
Если мы намереваемся обучить нейронную сеть с использованием градиентного спуска, нам нужна дифференцируемая функция активации. Поскольку единичная ступенчатая функция совместима с поведением биологических нейронов включен/выключен и теоретически эффективна (хотя и с ограничениями) в системах, состоящих из искусственных нейронов, имеет смысл рассмотреть функцию активации, которая похожа на единичную ступенчатую функцию, но которую можно дифференцировать. Наш поиск заканчивается на логистической сигмоидной функции.
Сигмоидная функция активации
Прилагательное «сигмоидная» относится к чему-то изогнутому в двух направлениях. Существуют различные сигмоидные функции, нас интересует только одна. Она называется логистической функцией, и математическое выражение для нее довольно простое:
\[f(x)=\frac{L}{1+e^{-kx}}\]
Константа L определяет значение максимума кривой, а константа k влияет на крутизну перехода. На графике ниже показаны примеры логистической функции для разных значений L, а на следующем графике показаны кривые для разных значений k.
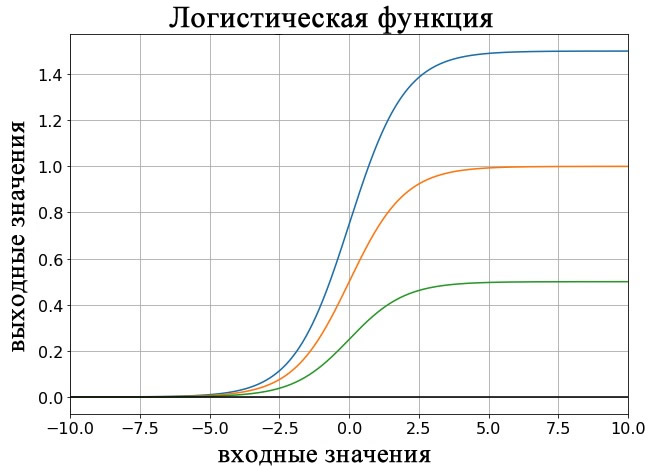
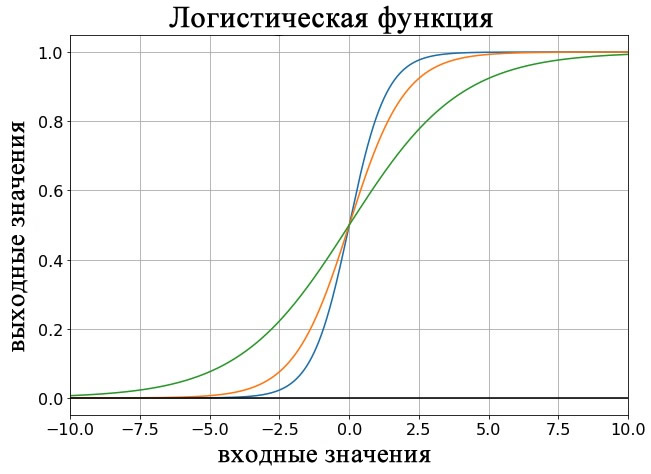
Логистическая функция – это не единственная функция активации, используемая в MLP (многослойных перцептронах), но она очень распространена и имеет несколько преимуществ:
- Как упоминалось выше, логистическая активация является превосходным улучшением единичной ступенчатой функции, потому что их общее поведение эквивалентно, но сглаженность в переходной области гарантирует, что функция непрерывна и, следовательно, дифференцируема.
- Вычислительная нагрузка, безусловно, превышает нагрузку от единичной ступенчатой функции, но она всё еще кажется мне вполне разумной – только одна операция возведения числа e в степень, одно сложение и одно деление.
- Мы можем легко настроить связь вход-выход, подстроив параметры L и k. Однако я считаю, что нейронные сети обычно используют стандартную логистическую функцию, то есть с L = 1 и k = 1.
- Форма логистической кривой (высокое значение производной вблизи середины диапазона выходных значений и низкое значение производной для выходных значений вблизи максимума и минимума) может способствовать успешному обучению. Я не могу претендовать на авторитетную экспертизу в таких вопросах, поэтому приведу цитату из книги по параллельной распределенной обработке, выпущенной Стэнфордским университетом: поскольку изменения веса пропорциональны производной функции активации, то они будут больше для узлов, которые «еще не решили, быть включенными или выключенными», и это может «[способствовать] стабильности обучения системы».
Производная логистической функции
Стандартная логистическая функция f(x) имеет следующую первую производную:
\[f(x)=\frac{1}{1+e^{-x}} \ \ \Rightarrow \ \ f^\prime(x)=\frac{e^x}{(1+e^x)^2}\]
Однако, если вы уже рассчитали выходное значение логистической функции для заданного входного значения, вам не нужно использовать выражение для производной, поскольку оказывается, что производная логистической функции связана с исходной логистической функцией следующим образом:
\[f^\prime(x)=f(x)(1-f(x))\]
Заключение
Я надеюсь, что теперь у вас есть четкое представление о том, что такое логистическая сигмоидная функция, и почему мы используем ее для активации в многослойных перцептронах. Логистическая функция, несомненно, эффективна, и я успешно использовал ее для проектирования нейронных сетей. Однако она становится менее подходящей по мере увеличения количества скрытых слоев из-за того, что называется проблемой исчезающего градиента. Возможно, мы рассмотрим проблему исчезающего градиента и другие более сложные вопросы в следующих статьях.
