Продвинутое машинное обучение с многослойным перцептроном
В данной статье объясняется, почему высокопроизводительным нейронным сетям требуется дополнительный «скрытый» слой вычислительных узлов.
Если вы заинтересованы в изучении нейронных сетей, вы попали в нужное место. Эта серия статей проведет вас через терминологию нейронных сетей, примеры нейросетей и общую теорию. Выше, в меню с содержанием, вы можете ознакомиться с остальными статьями из серии.
Пока что мы фокусировались на однослойном перцептроне, который состоит из входного слоя и выходного слоя. Как вы, возможно, помните, мы используем термин «однослойный», потому что эта конфигурация включает в себя только один слой вычислительно активных узлов, то есть узлов, которые изменяют данные путем суммирования, а затем применяют функцию активации. Узлы входного слоя просто распределяют данные.
Однослойный перцептрон, в принципе, прост, и процедура его обучения тоже проста. К сожалению, он не предлагает функциональность, которая нам нужна для сложных, реальных приложений. У меня сложилось впечатление, что стандартным способом объяснения фундаментальных ограничений однослойного перцептрона является использование логических операций в качестве наглядных примеров, и именно этот подход я буду использовать в этой статье.
Нейросетевой логический элемент
Есть что-то смешное в идее, что мы будем использовать чрезвычайно сложный микропроцессор для реализации нейронной сети, которая выполняет то же самое, что и схема, состоящая из нескольких транзисторов. Однако размышление о проблеме с этой стороны подчеркивает несоответствие однослойного перцептрона как инструмента для общей классификации и аппроксимации функций – если наш перцептрон не может воспроизвести поведение одного логического элемента, то нам нужно найти перцептрон получше.
Давайте вернемся к конфигурации системы, которая была представлена в первой статье этой серии.
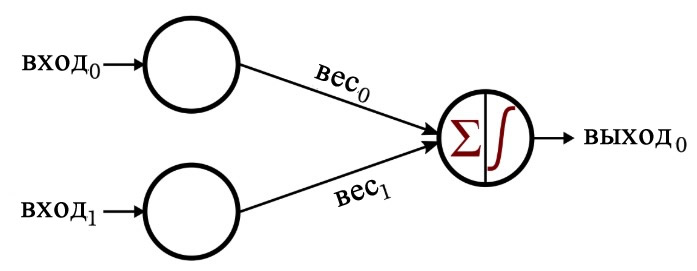
Общий вид этого перцептрона напоминает мне логический элемент, и это действительно так. Допустим, мы обучаем эту нейросеть с помощью выборок элементов входного вектора, состоящих из нулей и единиц, и выходного значения, равного единице, только если оба входных значения равны единице. Результатом будет нейронная сеть, которая классифицирует входной вектор способом, аналогичным электрическому поведению логического элемента И (AND).
Размерность входных данных этой нейросети равна 2, поэтому мы можем легко построить входные выборки в двухмерном графике. Допустим, что вход0 соответствует горизонтальной оси, а вход1 соответствует вертикальной оси. Четыре возможные комбинации входных значений будут расположены следующим образом:
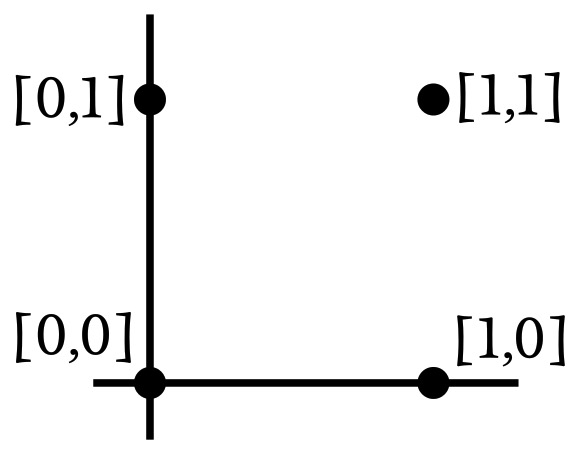
Поскольку мы повторяем операцию И, нейросети необходимо изменить свои веса таким образом, чтобы выходное значение было равно единице для входного вектора [1,1] и нулю для остальных трех входных векторов. Основываясь на этой информации, давайте разделим пространство входных значений на секции, соответствующие требуемым классификациям выходных значений:
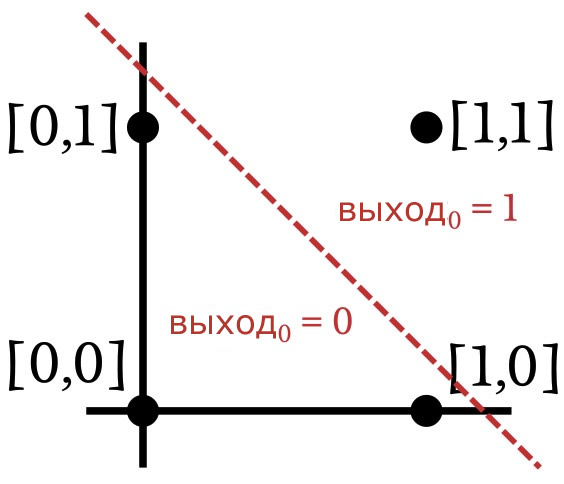
Линейно разделимые данные
Как показано на предыдущем графике, когда мы реализуем операцию И, входные векторы, построенные на графике, можно классифицировать, нарисовав прямую линию. Всё с одной стороны линии получает выходное значение, равное единице, а всё на другой стороне – нулевое выходное значение. Таким образом, в случае операции И данные, которые представлены в нейросети, являются линейно разделимыми. Это также относится к операции ИЛИ:
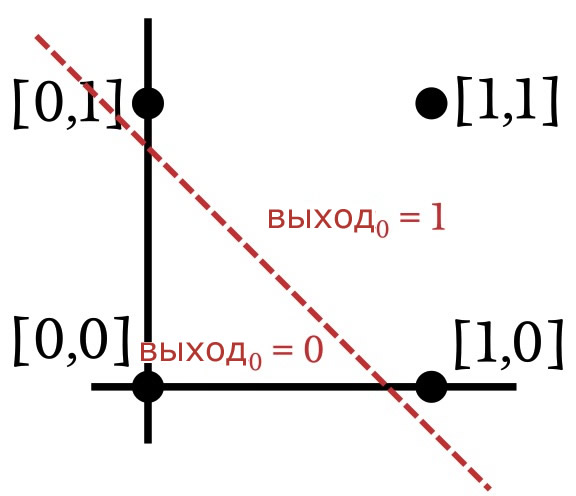
Оказывается, что однослойный перцептрон может решить задачу, только если данные линейно разделимы. Это верно независимо от размерности входных выборок. Двумерный случай легко визуализировать, потому что мы можем построить точки и разделить их линией. Чтобы обобщить концепцию линейной разделимости, вместо «линии» мы должны использовать слово «гиперплоскость». Гиперплоскость – это геометрический объект, который может разделять данные в n-мерном пространстве. В двумерной среде гиперплоскость является одномерным объектом (то есть линией). В трехмерной среде гиперплоскость – это обычная двумерная плоскость. В n-мерной среде гиперплоскость имеет (n-1) измерений.
Решение задач, которые не являются линейно разделимыми
Во время процедуры обучения однослойный перцептрон использует обучающие выборки, чтобы выяснить, где должна находиться гиперплоскость классификации. После того, как он находит гиперплоскость, которая надежно разделяет данные на правильные категории классификации, он готов к работе. Однако перцептрон не найдет эту гиперплоскость, если она не существует. Давайте рассмотрим пример связи вход-выход, которая не является линейно разделимой:
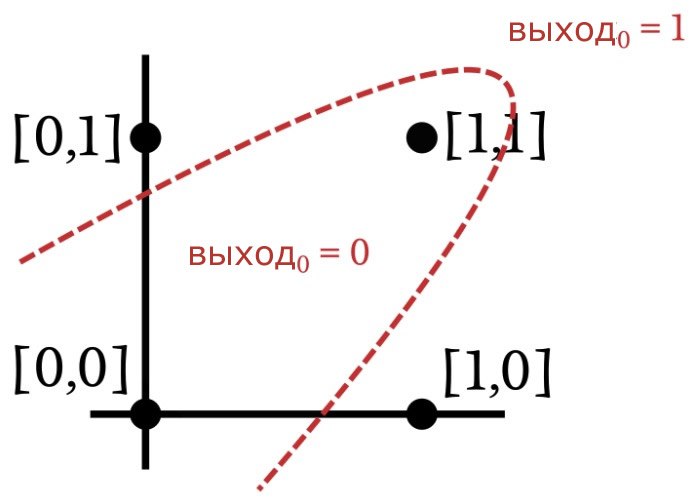
Узнаете эту связь? Посмотрите еще раз, и вы увидите, что это не что иное, как операция «исключающее ИЛИ» (или сложение по модулю 2, или XOR). Вы не можете разделить данные «исключающего ИЛИ» с помощью прямой линии. Таким образом, однослойный перцептрон не может реализовать функциональность, предоставляемую логическим элементом «исключающее ИЛИ». И, если он не может выполнить операцию «исключающее ИЛИ», мы можем с уверенностью предположить, что задачи многих других (гораздо более интересных) приложений будут вне досягаемости для решения при возможностях однослойного перцептрона.
К счастью, мы можем значительно увеличить способности нейросети решать задачи, просто добавив один дополнительный слой узлов. Это превращает однослойный перцептрон в многослойный перцептрон (MLP, multi-layer perceptron). Как упоминалось в предыдущей статье, этот слой называется «скрытым», поскольку он не имеет прямого интерфейса с внешним миром. Я полагаю, вы могли бы думать о MLP как о пресловутом «черном ящике», который принимает входные данные, выполняет загадочные математические операции и создает выходные данные. Скрытый слой находится внутри этого черного ящика. Вы не можете его видеть, но он есть.
Заключение
Добавление в перцептрон скрытого слоя – это довольно простой способ значительно улучшить систему в целом, но мы не можем ожидать, что получим все это улучшение даром. Первый недостаток, который приходит на ум, заключается в том, что обучение становится более сложным, и эту проблему мы рассмотрим в следующей статье.
