Формулы обучения и обратное распространение для многослойных перцептронов

В данной статье представлены формулы, которые мы используем при выполнении вычислений для обновления весовых коэффициентов, а также мы обсудим концепцию обратного распространения.

Добро пожаловать в серию статей по машинному обучению. С остальными статьями серии вы можете ознакомиться в меню с содержанием в начале статьи.

Мы достигли того момента, когда нам нужно тщательно рассмотреть фундаментальную тему теории нейронных сетей: вычислительную процедуру, которая позволяет нам точно настроить веса многослойного перцептрона (MLP, multilayer perceptron), чтобы он мог точно классифицировать входные выборки. Это приведет нас к концепции «обратного распространения», которая также является важным аспектом проектирования нейронных сетей.

Обновление весов

Информационная среда обучения для MLP сложна. Что еще хуже, онлайн-ресурсы используют различную терминологию и обозначения, и, похоже, они даже дают разные результаты. Однако я не уверен, что результаты действительно разные или просто представляют одну и ту же информацию по-разному.

Формулы, содержащиеся в этой статье, основаны на выводах и объяснениях, предоставленных доктором Дастином Стэнсбери в этом посте в блоге. Его объяснение – лучшее, что я нашел, и это отличное место для начала, если вы хотите углубиться в математические и базовые детали градиентного спуска и обратного распространения.

Следующая диаграмма представляет архитектуру, которую мы реализуем в программном обеспечении, и приведенные ниже формулы соответствуют этой архитектуре, которая более подробно обсуждается в следующей статье.

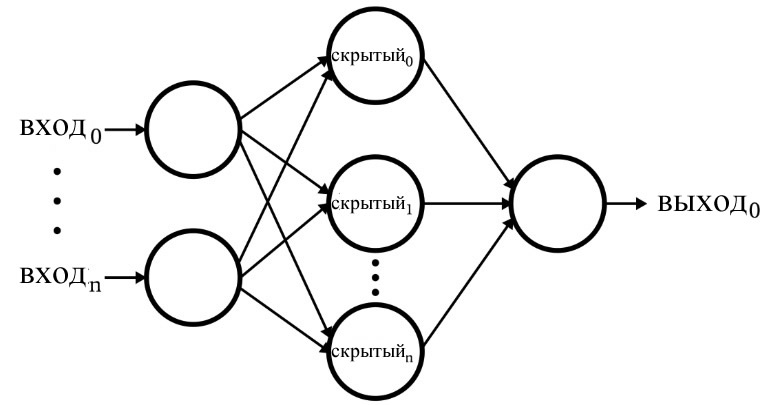
Терминология

Эта тема быстро станет неуправляемой, если мы не будем придерживаться четкой терминологии. Я буду использовать следующие термины:

• Преактивация (сокращенно \(S_{preA}\)): Это относится к сигналу (на самом деле это просто число в контексте одной обучающей итерации), который служит входным для функции активации узла. Он рассчитывается путем выполнения скалярного произведения массива, содержащего веса, и массива, содержащего значения, исходящие из узлов в предыдущем слое. Скалярное произведение эквивалентно выполнению поэлементного умножения двух массивов и затем суммированию элементов массив, полученного в результате этого умножения.
• Постактивация (сокращенно \(S_{postA}\)): Это относится к сигналу (опять же, просто число в контексте отдельной итерации), который выходит из узла. Он создается путем применения функции активации к сигналу преактивации. Я предпочитаю обозначение функции активации \(f_{A}()\), это логистическая сигмоидная функция.
• В коде на Python вы увидите весовые матрицы, помеченные как ItoH и HtoO. Я использую эти идентификаторы, потому что фраза «веса скрытого слоя» будет неоднозначной – это будут веса, которые применяются до или после скрытого слоя? В моей схеме ItoH указывает веса, которые применяются к значениям, передаваемым из входных узлов в скрытые узлы (ItoH – Input toHidden), а HtoO определяет веса, которые применяются к значениям, передаваемым из скрытых узлов в выходной узел (HtoO – Hidden toOutput).
• Правильное выходное значение для обучающей выборки называется целью и обозначается буквой T (Target).
• Скорость обучения сокращенно обозначается как LR (Learning Rate).
• Конечная ошибка (FE – Final Error) – это разница между сигналом постактивации от выходного узла (\(S_{postA,O}\)) и целью, рассчитывается как \(FE = S_{postA,O}-T\).
• Сигнал ошибки (\(S_{ошибки}\)) – это последняя ошибка, распространяемая обратно к скрытому слою через функцию активации выходного узла.
• Градиент представляет вклад заданного веса в сигнал ошибки. Мы изменяем веса, вычитая этот вклад (умноженный на скорость обучения, если необходимо).

Некоторые из этих терминов показаны на следующей диаграмме конфигурации нейросети. Я знаю, это выглядит как разноцветный бардак. Приношу извинения. Это насыщенная информацией диаграмма, и, если вы внимательно ее изучите, я думаю, что вы найдете ее очень полезной.

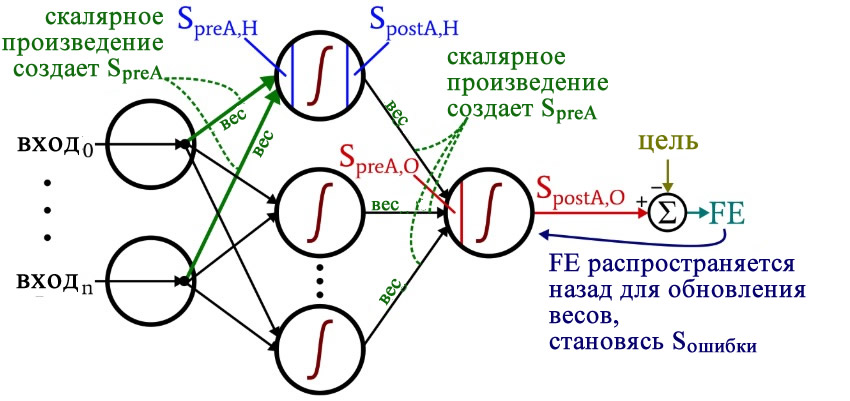
Формулы обновления весовых коэффициентов получаются путем взятия частной производной функции ошибки (мы используем среднюю квадратичную ошибку) относительно веса, который необходимо изменить. Если вы хотите посмотреть математику, обратитесь к посту доктора Стэнсбери; в данной статье мы перейдем непосредственно к результатам. Для весов от скрытых узлов к выходным узлам (HtoO) мы имеем следующее:

\[S_{ошибки} = FE \times {f_A}'(S_{preA,O})\]

\[градиент_{HtoO}= S_{ошибки}\times S_{postA,H}\]

\[вес_{HtoO} = вес_{HtoO}- (LR \times градиент_{HtoO})\]

Мы рассчитываем сигнал ошибки путем умножения конечной ошибки на значение, которое получается, когда мы берем производную функции активации по сигналу преактивации, доставляемому на выходной узел (обратите внимание на штрих, который означает первую производную, в \({f_A}'(S_{preA,O})\)). Затем вычисляется градиент путем умножения сигнала ошибки на сигнал постактивации из скрытого слоя. Наконец, мы обновляем вес, вычитая этот градиент из текущего значения веса, и, если мы хотим изменить размер шага, то можем умножить градиент на скорость обучения.

Для весов от входных узлов к скрытым узлам (ItoH) мы имеем следующее:

\[градиент_{ItoH} = FE \times {f_A}'(S_{preA,O})\times вес_{HtoO} \times {f_A}'(S_{preA,H}) \times вход\]

\[\Rightarrow градиент_{ItoH} = S_{ошибки} \times вес_{HtoO} \times {f_A}'(S_{preA,H})\times вход\]

\[вес_{ItoH} = вес_{ItoH} - (LR \times градиент_{ItoH})\]

Для весов от входных узлов к скрытым узлам ошибка должна распространяться обратно через дополнительный слой, и мы делаем это путем умножения сигнала ошибки на вес между скрытым и выходным узлами, соединенный с интересующим скрытым узлом. Таким образом, если мы обновляем вес между входным и скрытым узлами, который ведет к первому скрытому узлу, мы умножаем сигнал ошибки на вес, который соединяет первый скрытый узел с выходным узлом. Затем мы завершаем вычисление, выполняя умножения, аналогичные умножениям обновления весов между скрытыми и выходными узлами: мы берем производную функции активации по сигналу преактивации скрытого узла, а «входное» значение можно рассматривать как сигнал постактивации от входного узла.

Обратное распространение

Приведенное выше объяснение уже коснулось концепции обратного распространения. Я просто хочу кратко подкрепить эту концепцию, а также убедиться, что вы точно познакомились с этим термином, часто появляющимся в обсуждениях нейронных сетей.

Обратное распространение позволяет нам преодолеть дилемму скрытого узла, упоминаемую в восьмой статье. Нам необходимо обновить веса между входными и скрытыми узлами на основе разницы между сгенерированным выходным сигналом нейросети и целевыми выходными значениями, предоставленными обучающими данными, но эти веса влияют на сгенерированное выходное значение косвенно.

Обратное распространение относится к способу, с помощью которого мы отправляем сигнал ошибки обратно к одному или нескольким скрытым слоям и масштабируем этот сигнал ошибки, используя как веса, идущие из скрытого узла, так и производную функции активации скрытого узла. Итоговая процедура служит способом обновления веса на основе вклада этого веса в выходную ошибку, даже если этот вклад скрыт косвенной связью между весом между входным и скрытым узлами и сгенерированным выходным значением.

Заключение

Мы рассмотрели много важных материалов. Я думаю, что в этой статье у нас есть действительно ценная информация об обучении нейронным сетям, и надеюсь, что вы согласны. Серия станет еще более интересной, поэтому следите за обновлениями.

Теги