Как обучить нейронную сеть многослойный перцептрон
Мы можем значительно повысить производительность перцептрона, добавив слой скрытых узлов, но эти скрытые узлы также сделают обучение более сложным.
До сих пор в данной серии статей по нейронным сетям мы рассматривали классификацию данных с использованием нейронных сетей, в частности с перцептроном. Вы можете ознакомиться со статьями серии выше в меню с содержанием или сразу перейти к этой новой статье, которая объясняет основы нейронной сети многослойный перцептрон (MLP, multilayer perceptron).
Что из себя представляет нейронная сеть многослойный перцептрон?
Одна из предыдущих статей продемонстрировала, что однослойный перцептрон просто не может обеспечить производительность, которую мы ожидаем от современной архитектуры нейронных сетей. Система, ограниченная линейно разделяемыми функциями, не сможет аппроксимировать сложные связи вход-выход, которые возникают в реальных сценариях обработки сигналов. Решением является многослойный перцептрон (MLP), такой как этот:
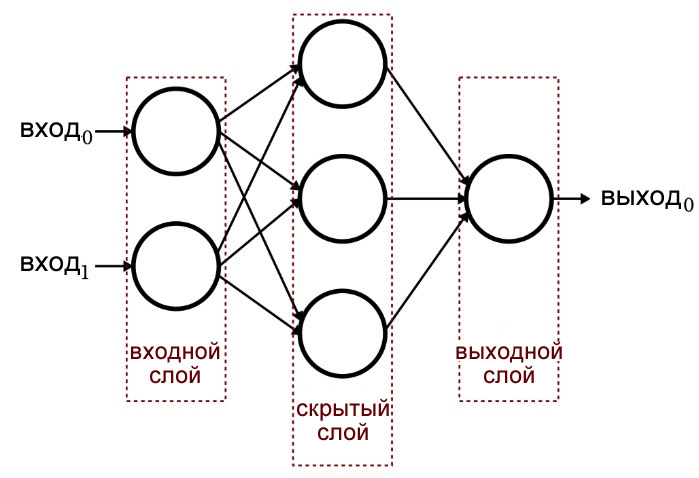
Добавляя этот скрытый слой, мы превращаем сеть в «универсальный аппроксиматор», который может выполнять чрезвычайно сложную классификацию. Но мы всегда должны помнить, что ценность нейронной сети полностью зависит от качества ее обучения. Без большого количества разнообразных обучающих данных и эффективной процедуры обучения нейросеть никогда не «научится» классифицировать входные выборки.
Почему скрытый слой усложняет обучение?
Давайте посмотрим на правило обучения, которое мы использовали для обучения однослойного перцептрона в предыдущей статье:
\[w_{новый} = w+(\alpha\times(выход_{ожидаемый}-выход_{рассчитанный})\times вход)\]
Обратите внимание на неявное предположение в этой формуле: мы обновляем весовые коэффициенты на основе наблюдаемого результата, поэтому, чтобы это работало, весовые коэффициенты в однослойном персептроне должны напрямую влиять на выходное значение. Это всё равно, что выбирать температуру воды в кране, поворачивая две ручки для горячей и холодной воды. Взаимосвязь между общей температурой и действием ручки довольно проста, и даже люди, которые не любят математику, могут найти желаемую температуру воды, немного покрутив ручки.
Но теперь представьте, что поток воды через горячие и холодные трубы связан с положением ручек сложным, крайне нелинейным образом. Вы постоянно и медленно поворачиваете ручку для горячей воды, но итоговый поток меняется беспорядочно. Вы пробуете повернуть ручку для холодной воды, и она делает то же самое. Установить идеальную температуру воды в этих условиях (особенно потому, что «результат» должен достигаться за счет сочетания двух запутанных управляющих связей) было бы гораздо сложнее.
Вот как я понимаю дилемму скрытого слоя. Веса, которые соединяют входные узлы со скрытыми узлами, в принципе, аналогичны этим механическим ручкам с беспорядочным поведением. Поскольку весовые коэффициенты между входным и скрытым слоями не имеют прямого пути к выходному слою, связь между этими весами и выходом нейросети настолько сложна, что простое правило обучения, показанное выше, будет неэффективным.
Новая парадигма обучения
Поскольку изначальное правило обучения перцептрона не может быть применено к многослойным сетям, нам необходимо пересмотреть нашу стратегию обучения. А точнее, мы собираемся включить градиентный спуск и минимизацию функции ошибки.
Следует иметь в виду, что эта процедура обучения не является специфичной для многослойных нейронных сетей. Градиентный спуск идет из общей теории оптимизации, и процедура обучения, которую мы используем для MLP, также применима к однослойным сетям. Однако насколько я понимаю, градиентный спуск в стиле MLP (по крайней мере теоретически) не нужен для однослойного перцептрона, потому что простое правило, показанное выше, в конечном итоге выполнит свою работу.
Получение действующих формул обновления весов для MLP включает в себя некоторую пугающую математику, которую я не буду пытаться подробно объяснить на данном этапе. Моя цель в оставшейся части этой статьи состоит в том, чтобы дать обобщенное введение в два ключевых аспекта обучения MLP (градиентный спуск и функция ошибки), и затем мы продолжим это обсуждение в следующей статье, добавив новую функцию активации.
Градиентный спуск
Как следует из названия, градиентный спуск – это средство снижения к минимуму функции ошибки, основанное на наклоне. На приведенной ниже диаграмме показано, как градиент дает нам информацию о том, как изменять веса. Наклон точки на графике функции ошибки говорит нам, в каком направлении нам нужно двигаться, и как далеко мы от минимума.
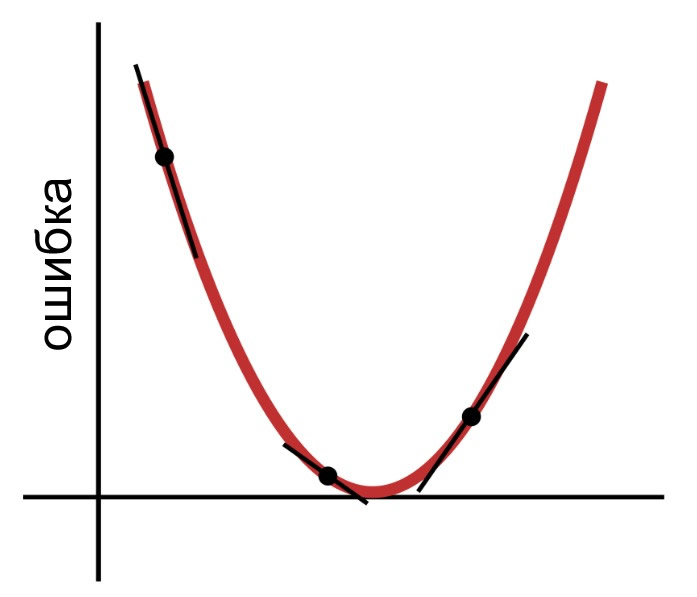
Таким образом, производная функции ошибки является важным элементом вычислений, которые мы будем использовать для обучения многослойного персептрона. На самом деле, нам здесь понадобятся частные производные. Когда мы реализуем градиентный спуск, мы делаем каждую модификацию веса пропорциональной наклону функции ошибки относительно модифицируемого веса.
Функция ошибки (aka функция потерь)
Общий метод количественного определения ошибки нейронной сети состоит в том, чтобы для каждого выходного узла возвести в квадрат разницу между ожидаемым (или «целевым») значением и рассчитанным значением, а затем суммировать все эти возведенные в квадрат разности. Вы можете назвать это «сумма квадратов разностей» или «сумма квадратов ошибок» или, возможно, как-то по-другому. И вы также увидите аббревиатуру LMS (least mean square), которая обозначает наименьшее среднеквадратичное значение (метод наименьших квадратов), потому что цель обучения состоит в том, чтобы минимизировать среднеквадратичное значение ошибки. Эта функция ошибки (обозначаемая E) может быть математически выражена следующим образом:
\[E=\frac{1}{2}\sum_k(t_k-o_k)^2\]
где k указывает диапазон выходных узлов, t является целевым выходным значением, а o является рассчитанным выходным значением.
Заключение
Мы заложили основу для успешного обучения многослойного перцептрона и продолжим исследовать эту интересную тему в следующей статье.
