Несколько примеров для цепей переменного тока

Давайте соединим последовательно три источника переменного напряжения и используем комплексные числа для определения итогового напряжения.

Все правила и законы, усвоенные при изучении цепей постоянного тока, применимы и к цепям переменного тока (закон Ома, законы Кирхгофа, методы анализа цепей), за исключением расчета мощности (закон Джоуля).

Единственное ограничение состоит в том, что все переменные должны быть выражены в комплексной форме с учетом фазы и амплитуды, и все напряжения и токи должны иметь одинаковую частоту (для того, чтобы их фазовые соотношения оставались постоянными).

Обозначения полярности всех трех источников напряжения ориентированы таким образом, чтобы их напряжения складывались в общее напряжение на резисторе нагрузки.

Обратите внимание, что, хотя для каждого источника переменного напряжения указаны амплитуда и угол фазы, значения частоты для них не указаны. Если это так, предполагается, что все частоты равны, что соответствует нашим требованиям для применения правил цепей постоянного тока к цепям переменного тока (все значения даны в комплексной форме, все на одной и той же частоте).

Формула для нахождения полного напряжения выглядит следующим образом:

\[E_{общ} = E_1 + E_2 + E_3\]

\[E_{общ} = (22В \angle -64^{\circ}) + (12В \angle 35^{\circ}) + (15В \angle 0^{\circ})\]

Графически векторы складываются, как показано на рисунке ниже.

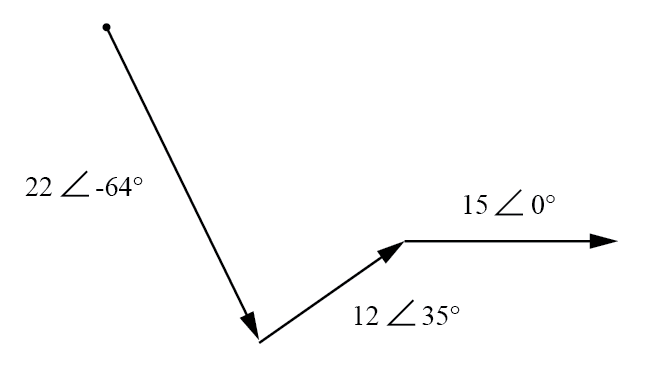
Сумма этих векторов будет результирующим вектором, начинающимся в начальной точке вектора 22 В (точка в верхнем левом углу диаграммы) и заканчивающимся в конечной точке вектора 15 В (остриё стрелки в середине по горизонтали, справа):

Чтобы определить величину и угол результирующего вектора, не прибегая к графическим изображениям, мы можем преобразовать каждое из этих комплексных чисел из полярной формы в алгебраическую форму, а затем сложить их.

Помните, что мы складываем эти значения вместе потому, что отметки полярности этих трех источников напряжения ориентированы аддитивным образом:

\[15 В \angle 0^{\circ} = 15 + j0 \ В\]

\[12 В \angle 35^{\circ} = 9,8298 + j6,8829 \ В\]

\[22 В \angle -64^{\circ} = 9,6442 - j19,7735 \ В\]

\[\begin{matrix} 15 +j0 \ В \\ 9,8298 + j6,8829 \ В\\ 9,6442 - j19,7735 \ В \\ \hline 34,4740 - j12,8906 \ В \end{matrix}\]

В полярной форме результат был равен 36,8052 вольт ∠-20,5018°. В реальном выражении это означает, что напряжение, измеренное на этих трех источниках напряжения, будет равно 36,8052 В, отставая от 15 В (опорная фаза 0°) на 20,5018°.

Вольтметр, подключенный к этим точкам в реальной цепи, будет показывать только амплитуду напряжения в полярной форме (36,8052 вольт), без значения угла. Для отображения двух сигналов напряжения может использоваться осциллограф и, таким образом, обеспечивать измерение сдвига фазы.

Тот же принцип справедлив и для амперметров переменного тока: они показывают амплитуду тока в полярной форме, без угла фазы.

Это чрезвычайно важно для соотнесения расчетных значений напряжения и тока с реальными цепями.

Хотя алгебраическая форма записи удобна для сложения и вычитания, и результат в нашем примере в конце был записан именно в этом виде, она не очень применима в практических измерениях.

Чтобы значения в алгебраической форме можно было связать с фактическими измерениями схемы, их необходимо преобразовать в полярную форму (а именно, для получения амплитуды в полярной форме).

Для проверки точности наших результатов мы можем использовать SPICE. В этой тестовой схеме номинал резистора 10 кОм выбран произвольно. Он добавлен, чтобы SPICE не выдавал ошибку о разрыве цепи и не прерывал анализ.

Кроме того, выбор частот напряжений для моделирования (60 Гц) тоже довольно произвольный, поскольку резисторы одинаково реагируют на все частоты переменного напряжения и тока. Существуют и другие компоненты (в частности, конденсаторы и катушки индуктивности), которые неодинаково реагируют на разные частоты, но это уже другая тема!

v1 1 0 ac 15 0 sin
v2 2 1 ac 12 35 sin
v3 3 2 ac 22 -64 sin
r1 3 0 10k
.ac link 1 60 60           
.print ac v(3,0) vp(3,0) 
.end

freq           v(3)           vp(3)
6.000E+01      3.681E+01      -2.050E+01

Разумеется, мы получаем общее напряжение 36,81 вольт ∠ -20,5° (относительно источника на 15 вольт, фаза которого была произвольно установлена равной нулю градусов, чтобы он был «эталонным» сигналом).

На первый взгляд это противоречит интуиции. Как можно получить общее напряжение чуть более 36 вольт при последовательном подключении источников питания на 15, 12 и 22 вольт? С цепями постоянного тока это было бы невозможно, поскольку значения напряжения будут напрямую складываться или вычитаться, в зависимости от полярности.

Но с цепями переменного тока наша «полярность» (сдвиг фазы) может варьироваться от полного сложения до полного вычитания, и в итоге получается такое парадоксальное суммирование.

Что, если мы возьмем ту же схему и перевернем один из источников напряжения? Тогда его вклад в общее напряжение будет противоположным тому, что было раньше (рисунок ниже):

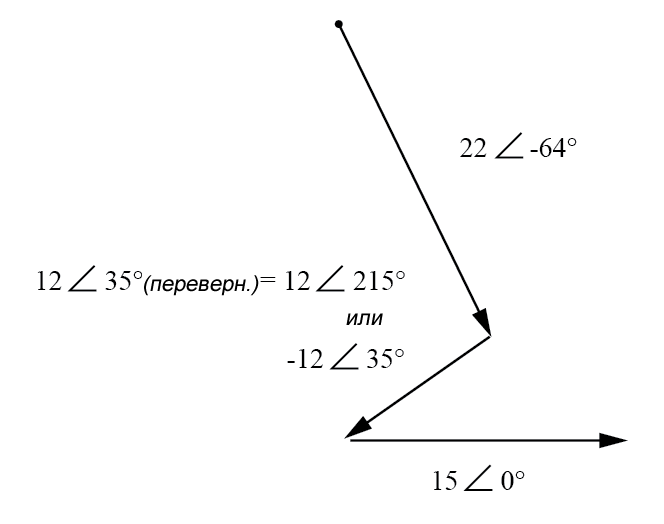
Обратите внимание, что угол фазы источника питания 12 В по-прежнему составляет 35°, даже если его выводы поменяны местами. Помните, что угол фазы любого падения напряжения указывается в соответствии с указанной полярностью. Несмотря на то, что угол по-прежнему записывается как 35°, вектор будет нарисован на 180° противоположно тому, что было раньше (рисунок ниже):

Результирующий вектор (сумма векторов) должен начинаться в верхней левой точке (начало вектора 22 вольта) и заканчиваться на конце стрелки вектора 15 вольт (рисунок ниже):

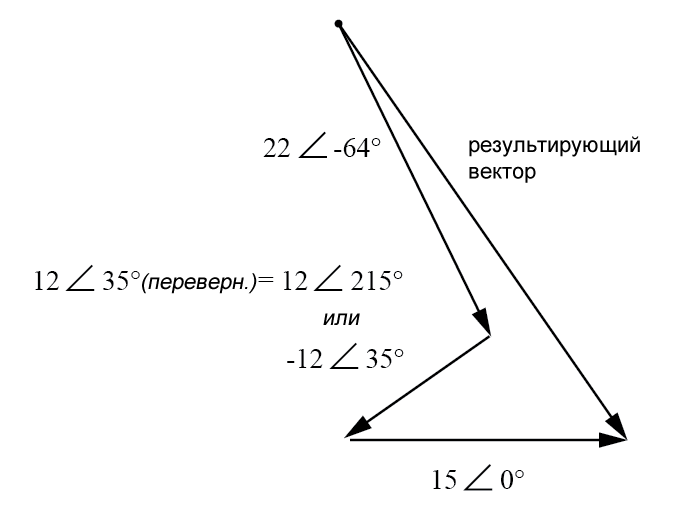
Изменение подключения источника 12 В в полярной форме может быть представлено двумя разными способами: добавлением 180° к углу его вектора (что составит 12 вольт ∠ 215°) или изменением знака амплитуды (что в итоге дает -12 вольт ∠ 35°). В любом случае преобразование в алгебраическую форму даст один и тот же результат:

\[\begin{matrix} 12 \angle 35^{\circ} \text{(в обратной полярности)} & = 12 \angle 215^{\circ} & = -9,8298-j6,8829 \\ & \text{или} \\ & = -12 \angle 35^{\circ} & = -9,8298-j6,8829 \end{matrix}\]

Полученная сумма напряжений в алгебраической форме тогда будет следующей:

\[\begin{matrix} 15 +j0 \ В \\ 9,8298 - j6,8829 \ В\\ 9,6442 - j19,7735 \ В \\ \hline 14,8143 - j26,6564 \ В \end{matrix}\]

В полярной форме это равно 30,4964 В ∠ -60,9368°. Еще раз воспользуемся SPICE для проверки результатов наших расчетов:

ac voltage addition 
v1 1 0 ac 15 0 sin      
v2 1 2 ac 12 35 sin    Обратите внимание на перемену местами номеров узлов 2 и 1     
v3 3 2 ac 22 -64 sin   для имитации переворачивания подключения
r1 3 0 10k      
.ac lin 1 60 60 
.print ac v(3,0) vp(3,0)
.end    

freq          v(3)        vp(3)       
6.000E+01     3.050E+01  -6.094E+01

Резюме

• Все законы и правила цепей постоянного тока применимы и к цепям переменного тока, за исключением расчета мощности (закон Джоуля), при условии, что все значения выражаются и обрабатываются в комплексной форме, а все напряжения и токи имеют одинаковую частоту.
• При изменении направления вектора на противоположное (что эквивалентно изменению полярности источника переменного напряжения по отношению к другим источникам напряжения), это может быть выражено двумя разными способами: добавлением 180° к углу фазы или изменением знака амплитуды.
• Показания измерительного прибора в цепи переменного тока соответствуют амплитудам в полярной форме расчетных значений. Алгебраические выражения комплексных величин в цепи переменного тока не имеют прямого эмпирического эквивалента, хотя они удобны для выполнения сложения и вычитания, как того требуют законы Кирхгофа для напряжений и токов.

Теги