Простые случаи сложения векторов
Помните, что векторы – это математические объекты, подобные числам на числовой прямой: их можно складывать, вычитать, умножать и делить. Сложение – это, пожалуй, самая простая для визуализации операция с векторами, поэтому мы начнем с нее. Если складываются векторы с одинаковыми углами, их величины (длины) складываются как обычные скалярные величины:

Точно так же, если источники переменного напряжения с одинаковым углом сдвига фаз соединены последовательно, их напряжения складываются, как если бы это были напряжения батарей:
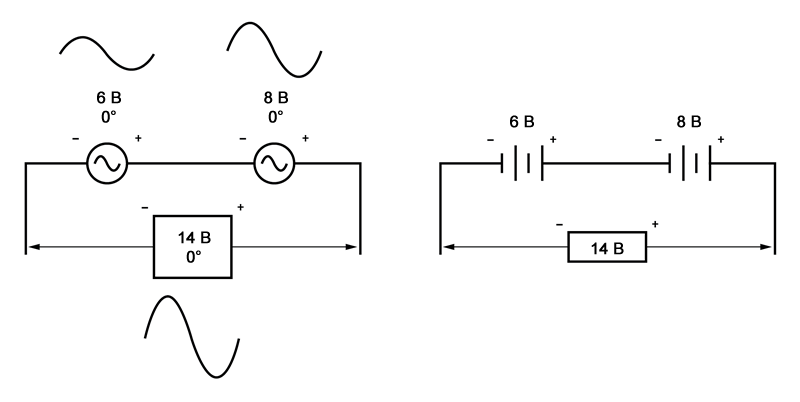
Обратите внимание на обозначения полярности (+) и (-) рядом с выводами двух источников переменного напряжения. Несмотря на то, что мы знаем, что переменный ток не имеет «полярности» в том же смысле, что и постоянный ток, эти обозначения важны, чтобы знать, как ссылаться на заданные фазовые углы напряжений. Это станет более очевидным в следующем примере.
Если складываются векторы, прямо противоположные друг другу (сдвинуты по фазе на 180°), их величины (длины) вычитаются так же, как при сложении вычитаются положительные и отрицательные скалярные величины:

Точно так же, если противоположные источники переменного напряжения включены последовательно, их напряжения вычитаются, как если бы это были напряжения батарей, включенных в противоположных направлениях:
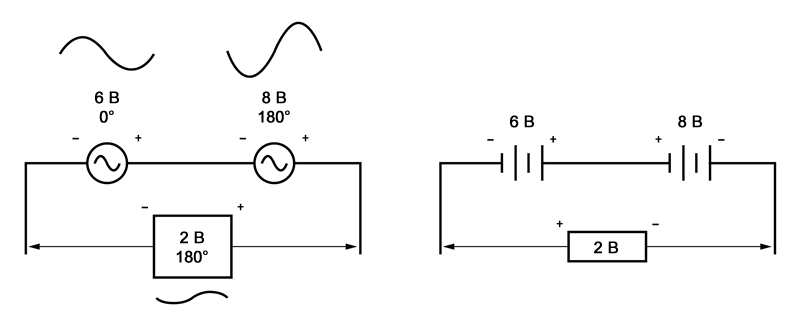
Чтобы определить, противоположны ли эти источники напряжения друг другу, необходимо проверить обозначение их полярности и их фазовые углы. Обратите внимание на то, как маркировка полярности на приведенной выше схеме, похоже, указывает на складывающиеся напряжения (слева направо мы видим - и + на источнике 6 В, - и + на источнике 8 В).
Несмотря на то, что эти обозначения полярности обычно указывают на аддитивный эффект в цепи постоянного тока (два напряжения работают вместе, чтобы создать большее общее напряжение), в этой схеме переменного тока они фактически работают в противоположных направлениях, потому что одно из этих напряжений имеет фазовый угол 0°, а другое – фазовый угол 180°.
В результате, естественно, получается полное напряжение 2 вольта.
С таким же успехом мы могли бы показать вычитание противоположных последовательных напряжений следующим образом:
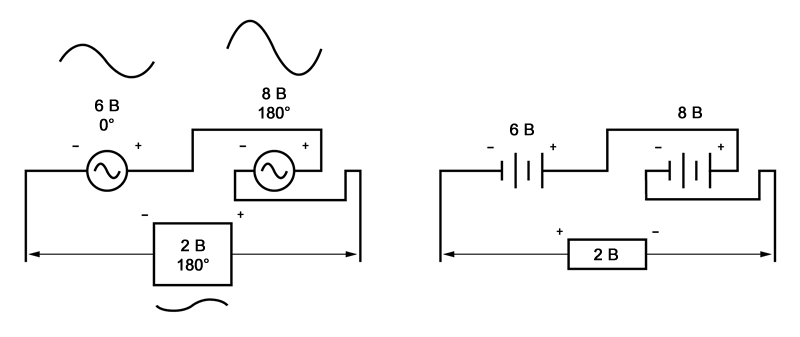
Обратите внимание на то, как полярности теперь кажутся противоположными друг другу из-за перестановки проводов на источнике 8 вольт.
Поскольку оба источника описываются как имеющие одинаковые фазовые углы (0°), они действительно противоположны друг другу, и общий эффект такой же, как и в предыдущем сценарии с «аддитивными» полярностями и разными фазовыми углами: общее напряжение всего 2 вольта.
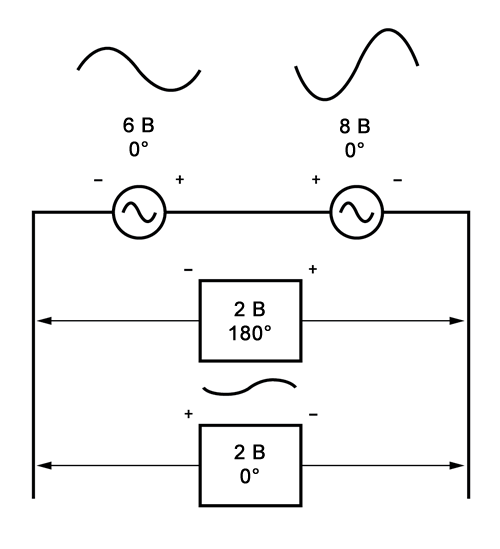
Результирующее напряжение может быть выражено двумя способами: 2 вольта при 180° со знаком (-) слева и знаком (+) справа, или 2 вольта при 0° со знаком (+) слева и знаком (-) справа. Переворачивание проводов на источнике переменного напряжения аналогично сдвигу фазы этого источника на 180°.

