Полярное и алгебраическое представления комплексных чисел
Чтобы работать с комплексными числами без рисования векторов, нам сначала нужно разобраться со стандартными математическими преставлениями. Существует две основных формы представления комплексных чисел: полярная и алгебраическая.
Полярное представление комплексного числа
Полярная форма – это когда комплексное число обозначается длиной (также известной как амплитуда, абсолютная величина или модуль) и углом его вектора (обычно обозначается символом угла, который выглядит следующим образом: ∠).
Если использовать аналогию с картой, полярное обозначение вектора из Нью-Йорка в Сан-Диего будет примерно таким: «2400 миль к юго-западу». Ниже показано несколько примеров векторов и их полярных обозначений:
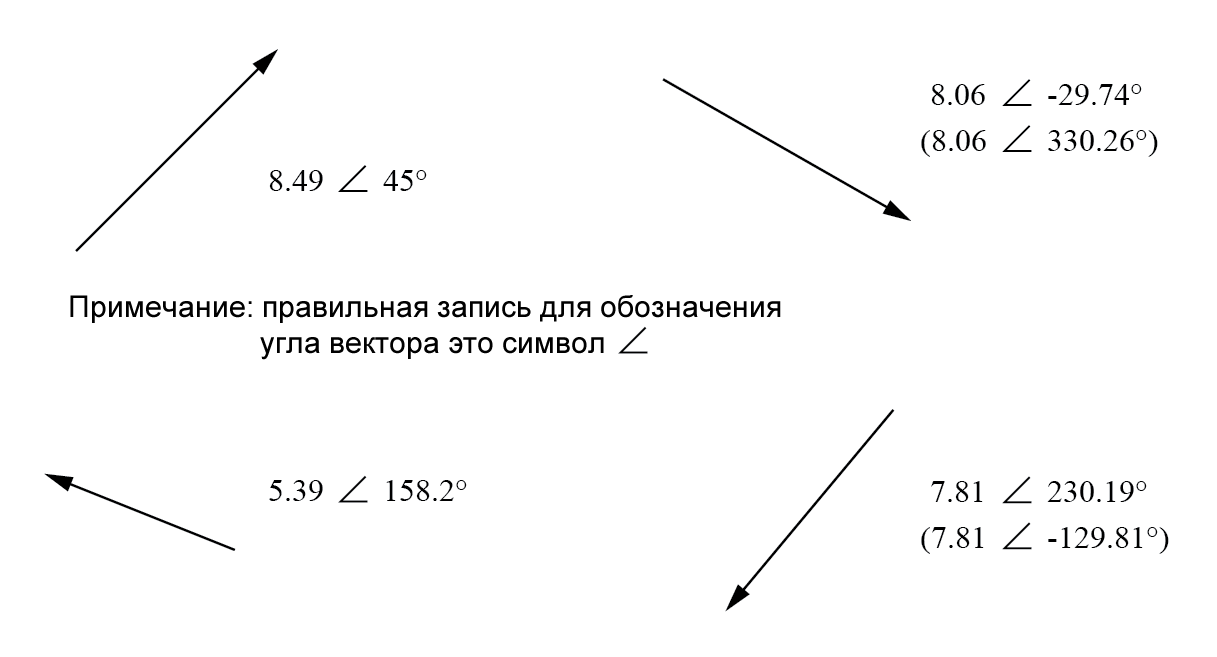
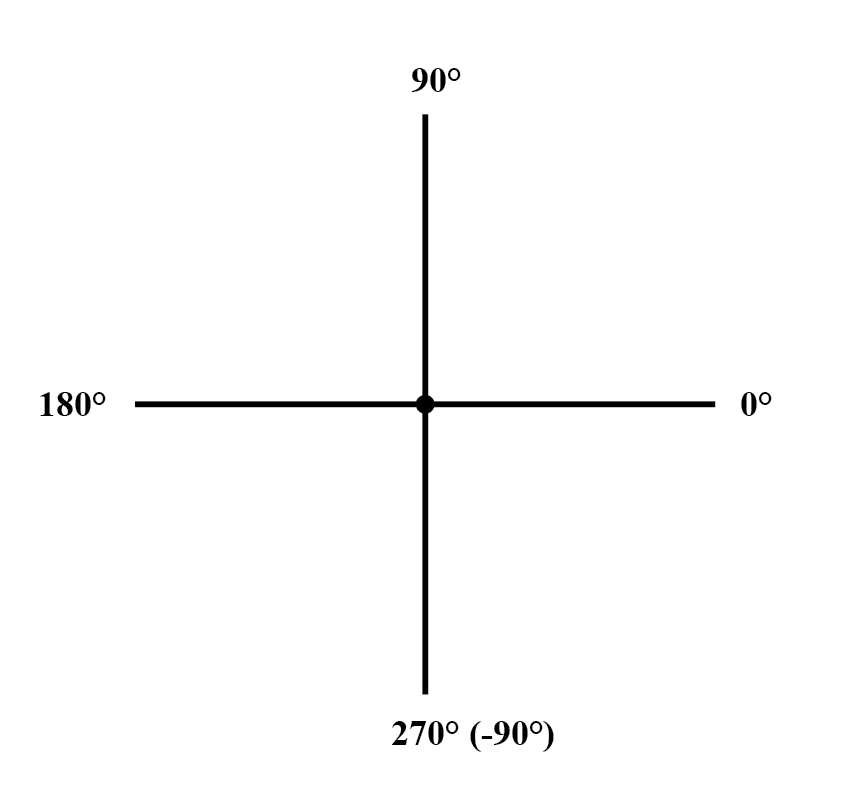
Стандартная ориентация углов векторов в расчетах цепей переменного тока определяет 0° как вправо (по горизонтали), то есть 90° – это непосредственно вверх, 180° – это влево, и 270° – это непосредственно вниз. Обратите внимание, что векторы, расположенные под углом «вниз», могут иметь углы, представленные в полярной форме как положительные значения, превышающие 180°, так и как отрицательные значения, меньшие 180°.
Например, про вектор с углом ∠ 270° (непосредственно вниз) также можно сказать, что он имеет угол -90°. Вектор на рисунке 1 нижний, правый (7,81 ∠ 230,19°) также можно обозначить как 7,81 ∠ -129,81°.
Алгебраическое представление комплексного числа
Алгебраическая форма – это когда комплексное число обозначается соответствующими горизонтальной и вертикальной составляющими. По сути, вектор считается гипотенузой прямоугольного треугольника, описываемого длинами прилежащего и противолежащего катетов.
Вместо того чтобы описывать длину и направление вектора с помощью обозначения амплитуды и угла, он описывается в терминах «как далеко влево/вправо» и «как далеко вверх/вниз».
Эти двумерные значения (по горизонтали и по вертикали) обозначаются двумя числами. Чтобы различать друг от друга эти значения по горизонтали и по вертикали, перед значением по вертикали ставится префикс в нижнем регистре «i» (в чистой математике) или «j» (в электронике).
Эти строчные буквы представляют не физическую переменную (такую как мгновенный ток, также обозначаемый строчной буквой «i»), они представляют собой математические операторы, используемые для различения вертикальной составляющей вектора от его горизонтальной составляющей. В полном представлении комплексного числа эти горизонтальные и вертикальные величины записываются в виде суммы (рисунок ниже):
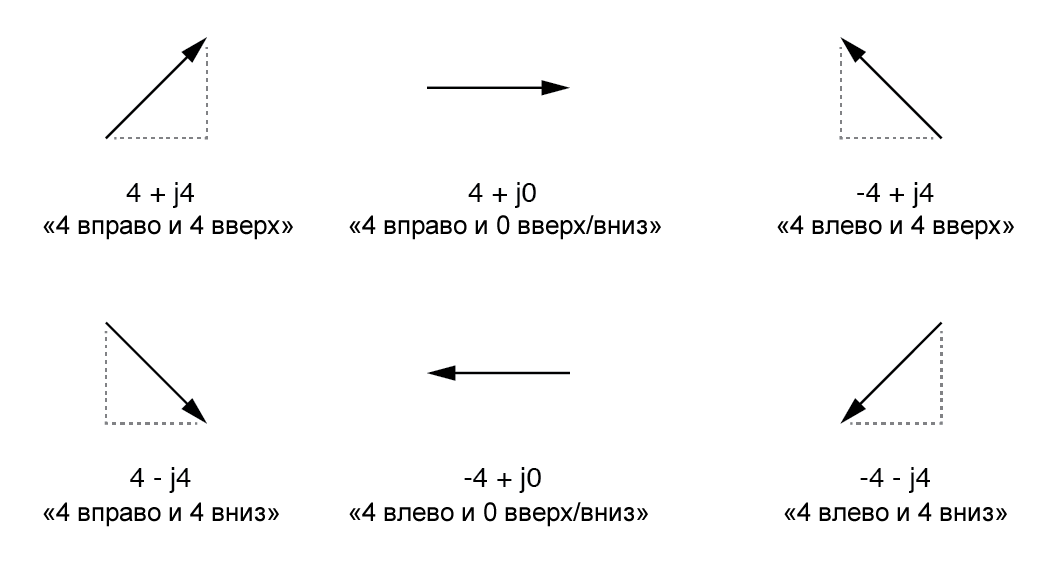
Горизонтальная составляющая называется действительной составляющей, поскольку это измерение совместимо с обычными скалярными («действительными») числами. Вертикальная составляющая называется мнимой, поскольку это измерение находится в другом направлении, совершенно чуждом шкале действительных чисел (рисунок ниже).
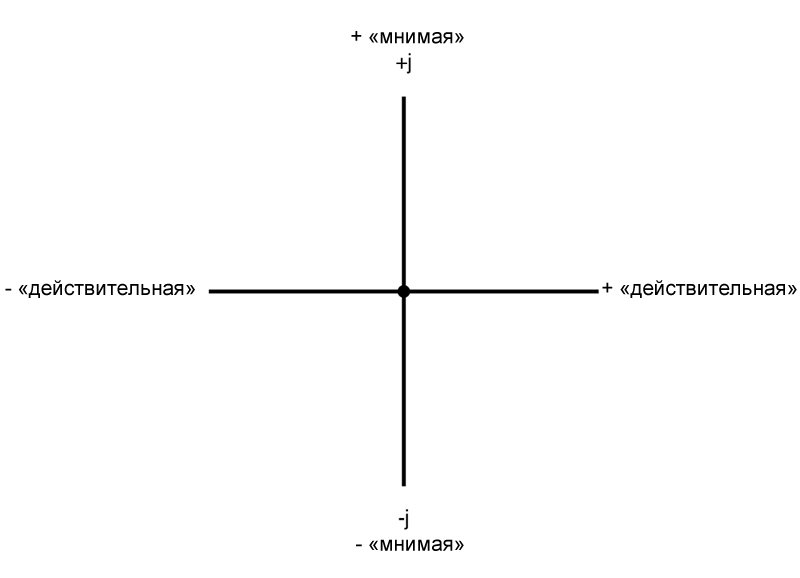
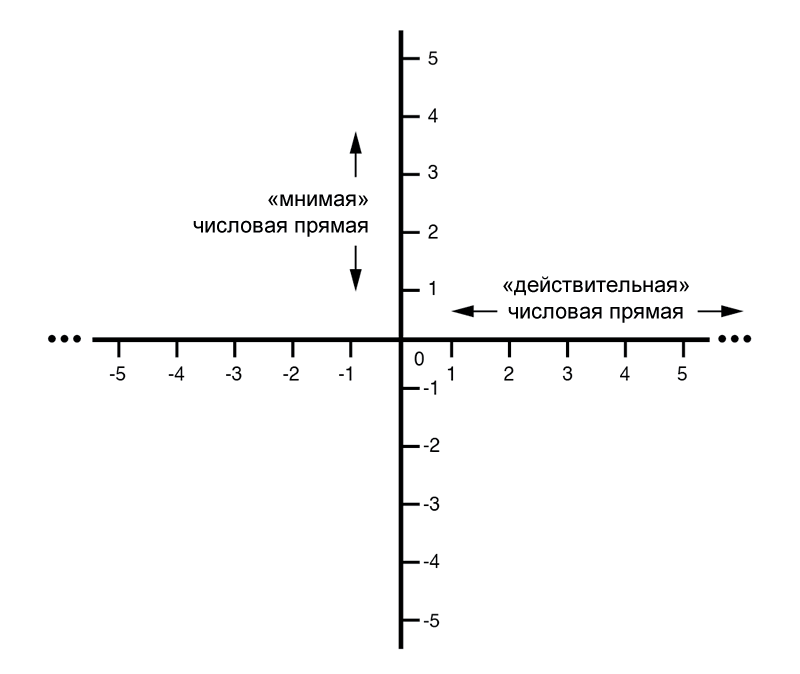
«Действительная» ось графика соответствует знакомой числовой прямой, которую мы видели ранее (с положительными и отрицательными значениями на ней). «Мнимая» ось графика соответствует другой числовой прямой, расположенной под углом 90° к «действительной».
Поскольку векторы являются двумерными объектами, для их представления у нас должна быть двухмерная «карта», т.е. две числовые прямые, перпендикулярные друг другу (рисунок ниже):
Преобразование из полярной формы в алгебраическую
Для комплексных чисел допустим любой метод записи. Основная причина наличия двух методов записи – простота вычислений вручную, алгебраическая форма позволяет использовать сложение и вычитание, а полярная форма позволяет использовать умножение и деление.
Преобразование между этими двумя формами записи требует использования простой тригонометрии. Чтобы преобразовать полярную форму в алгебраическую, найдите действительную составляющую, умножив амплитуду в полярной форме на косинус угла, и мнимую составляющую, умножив амплитуду в полярной форме на синус угла.
Это легче понять, если нарисовать значения как стороны прямоугольного треугольника, гипотенуза треугольника представляет сам вектор (его длина и угол по отношению к горизонтали – это полярная форма), горизонтальная и вертикальная стороны представляют собой соответственно «действительную» и «мнимую» алгебраические составляющие (рисунок ниже):
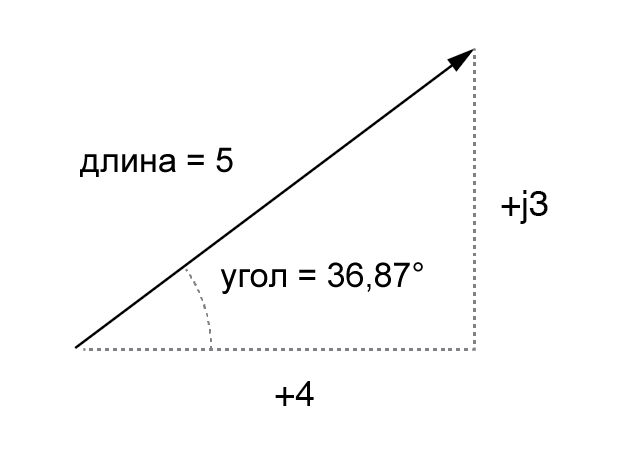
| 5 ∠ 36.87° | (полярная форма) |
| (5)(cos 36,87°) = 4 | (действительная составляющая) |
| (5)(sin 36,87°) = 3 | (мнимая составляющая) |
| 4 + j3 | (алгебраическая форма) |
Преобразование из алгебраической формы в полярную
Чтобы преобразовать алгебраическую форму в полярную, найдите амплитуду в полярной форме с помощью теоремы Пифагора (амплитуда в полярной форме – это гипотенуза прямоугольного треугольника, а действительная и мнимая составляющие являются соответственно прилежащим и противолежащим катетами), а угол, вычислив арктангенс результата деления мнимой составляющей на действительную составляющую:
| 4 + j3 | (алгебраическая форма) |
| \(c = \sqrt{a^2-b^2}\) | (теорема Пифагора) |
| \(амплитуда = \sqrt{4^2+3^2} = 5\) | |
| \(угол = \text{arctg}\frac{3}{4} = 36,87^\circ\) | |
| 5 ∠ 36.87° | (полярная форма) |
Резюме
- Полярная запись представляет комплексное число с точки зрения длины его вектора и угла направления от начальной точки. Пример: пролететь 45 миль ∠ 203° (запад на юго-запад).
- Алгебраическая запись представляет комплексное число с точки зрения его размеров по горизонтали и по вертикали. Пример: проехать 41 милю на запад, затем повернуть и проехать 18 миль на юг.
- В алгебраической записи первое значение – это «действительная» составляющая (размер вектора по горизонтали), а второе значение – «мнимая» составляющая (размер вектора по вертикали). Мнимой составляющей предшествует строчная буква «j», которую иногда называют оператором j.
- И полярная, и алгебраическая формы записи комплексного числа могут быть связаны графически в виде прямоугольного треугольника, где гипотенуза представляет сам вектор (полярная форма: длина гипотенузы = амплитуда; угол относительно горизонтальной стороны = угол), горизонтальная сторона представляет прямоугольный «действительную» составляющую, а вертикальная сторона представляет «мнимую» составляющую алгебраической формы записи.
